Навигация
3.1.3.2. Метод трапеций.
Метод трапеций был выбран по причине того, что схема Рунге основана на вычислении коэффициентов Фурье методом трапеций и является лишь результатом удачной манипуляции.. См. приложение 2.
3.1.3.3. Сравнение методов.
Если сравнивать две программы то необходимо заметить, что причиной того что мы отказались во второй программе от непосредственного применения схемы Рунге заключается в том, что она является довольно громоздкой и, несмотря на то, что схема Рунге требует меньшее количество вычислительных операций (
+2n), чем прямой метод трапеций (
), в то же время при вычислении на ЭВМ затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…).
Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании.
Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными методами он является более приемлемым. Способы его алгоритмизации были разработаны и подробно описаны в работе «Numerical recipes in C: The art of scientific computing»-Cambridge unv.,1992.
Сам алгоритм лишь упоминается в курсовой работе, потому что количество операций Б.П.Ф. сопоставимо со С.Р., только Б.П.Ф. является более гибким (в С.Р необходимо вводить n кратное 12-ти значений функции, а чтобы уменьшить погрешность необходимо вносить изменения в основную программу для увлечения количества исходных данных).
В дальнейшем я надеюсь продолжить изучение и разработку методов определения коэффициентов Фурье.
4. Заключение.
Можно сделать вывод, что ряды Фурье широко применяются в инженерно-технических расчетах. Они часто встречаются при рассмотрении ряда задач измерительной техники, особенно при исследовании колебательных процессов в измерительных системах, а также при анализе результатов измерений нестационарных параметров.
Алгоритмы, рассмотренных методы, достаточно строги, для того, чтобы их без проблем можно было перенести на ЭВМ. Составленные программы позволяют решить главную задачу - нахождение коэффициентов при аппроксимации функции. Сравнительный анализ показал, что оба рассмотренных метода имеют свои плюсы и минусы, и имеют право на существование.
5. Список литературы.
Фихтенгольц Г. М. «Курс дифференциального и интегрального исчисления»(III том) – Москва, 1970г.
БахваловН.С. «Численые методы» - Москва, 2002г.
Зедгинидзе Г.П., Гогсадзе Р.Ш. «Математические модели в измерительной технике» - Москва, 1970г.
Приложение 1.
{Схема Рунге для 12-ти орт:}
Program MetodRunge;
uses crt;
type ord1=array [0..11] of real;
var Y,U,V,S:ord1;
A:array [0..3] of real;
B:array [1..3] of real;
i,k:integer;
{процедура расчета сумм и разностей значений функции:}
Procedure SummaRaznost(X:ord1;var Sum:ord1;var Raz:ord1;j:integer);
var m:integer;
begin
m:=j*2+1;
for i:=1 to j do
begin
sum[i]:=X[i]+X[m];
raz[i]:=X[i]-X[m];
m:=m-1;
end;
sum[j+1]:=X[j+1];
end;
begin
clrscr;
{Ввод данных:}
writeln('Введите через пробел значения 12-ти, равноотстоящих на pi/6, значений функции');
for i:=0 to 11 do read(Y[i]);
{Расчет значений u и v:}
SummaRaznost(Y,U,V,5);
U[0]:=Y[0];
{Сдвиг всех элементов:u на одну ячейку вправо, чтобы на использовать нулевой элемент матрицы(вообще нулевой элемент будет использоваться только в матрице Y)}
for i:=7 downto 1 do
U[i]:=U[i-1];
{Расчет значений s и d (значения d заносятся в матрицу Y):}
SummaRaznost(U,S,Y,3);
{Расчет 0-го и 2-го коэффициентов:a, на основе полученных значений s:}
A[0]:=(S[1]+S[2]+S[3]+S[4])/12;
A[2]:=(S[1]-S[4]+0.5*(S[2]-S[3]))/6;
{ Расчет 1-го и 3-го коэффициентов:a, на основе полученных значений d:}
A[1]:=(Y[1]+0.886*Y[2]+0.5*Y[3])/6;
A[3]:=(Y[1]-Y[3])/6;
{Расчет значений sigma и delta(начения sigma заносятся в матрицу Y, delta в U):}
SummaRaznost(V,Y,U,2);
{Расчет 1 и 3-го коэффициентов:b, на основе полученных значений sigma:}
B[1]:=(0.5*Y[1]+0.886*Y[2]+Y[3])/6;
B[3]:=(Y[1]-Y[3])/6;
{ Расчет 2-го коэффициентов:b, на основе полученных значений delta:}
B[2]:=0.886*(U[1]+U[2])/6;
{Вывод разложения функции в ряд Фурье:}
writeln('Ответ:');
write('T=',A[0]:7:3);
for i:=1 to 3 do begin
if A[i]<0 then write(A[i]:7:3)
else write('+',A[i]:7:3);
write('cos',i,'x');
if B[i]<0 then write(B[i]:7:3)
else write('+',B[i]:7:3);
write('sin',i,'x');
end;
end.
Приложение 2.
{Метод трапеций:}
Program MetTrapecyi;
uses crt;
const pi=3.14;
type ord=array [0..5] of real;
var A,B:ord;
Y:array [0..23] of real;
h,eps:real;
m,i,k:integer;
{Функция расчета m-го коэффициента:а}
function af(n:integer;m:integer):real;
var res:real;
begin
res:=0;
for i:=0 to (n-1) do
res:=res+y[i]*cos(m*i*h);
af:=res*2/n;
end;
{Функция расчета m-го коэффициента b :}
function bf(n:integer;m:integer):real;
var res:real;
begin
res:=0;
for i:=0 to (n-1) do
res:=res+y[i]*(sin(m*i*h));
bf:=res*2/n;
end;
begin
clrscr;
writeln('интервал интегрирования: от 0 до 2pi');
{Ввод данных:}
writeln('Введите количество шагов ');
read(k);
writeln(' Введите значения функции с шагом 2pi/',k);
for i:=0 to (k-1) do
read(Y[i]);
{h-шаг метода}
h:=(2*pi)/k;
for m:=0 to 5 do begin
A[m]:=af(k,m);
B[m]:=bf(k,m);
end;
{Вывод результата.}
writeln('Отает: ');
writeln('a0=',A[0]/2);
for i:=1 to 5 do
writeln('a',i,'=',A[i]:5:4);
for i:=1 to 5 do
writeln('b',i,'=',B[i]:5:4);
end.
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Похожие работы
... . Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала. 2.Численные методы расчетов спектральных и временных характеристик периодических сигналов Для расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить ...
... , либо функция задана таблично , нахождение интеграла по формуле Ньютона-Лейбница невозможно. Используют приближенные формулы, которые называют квадратурными, либо формулами численного интегрирования. 1) Формулы прямоугольника Пусть y=f(x) непрерывна на [a,b]. Требуется вычислить . Разобьем отрезок интегрирования на n равных частей, точками xi, i=0,n xi=a-i*h шаг ...
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...
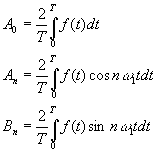
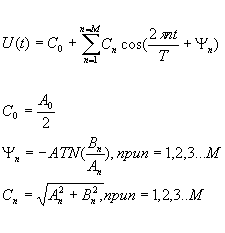
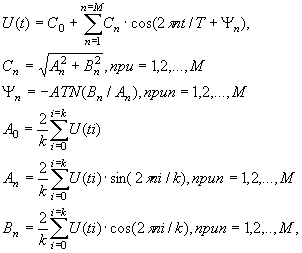
0 комментариев