Навигация
Спектральная теорема. Пусть Н – сепарабельное гильбертово пространство, тогда справедлива следующая теорема
2.2. Спектральная теорема. Пусть Н – сепарабельное гильбертово пространство, тогда справедлива следующая теорема.
Теорема 2.3. (спектральная теорема в форме операторов умножения). Паре ортопроекторов Р1 и Р2 в сепарабельном гильбертовом пространстве Н соответствует разложение
Н = Н0,0![]() Н0,1
Н0,1![]() Н1,0
Н1,0 ![]() Н1,1
Н1,1![]() (
(![]() (С2
(С2![]() L2((0,
L2((0, ![]() ), dρк)))
(2.4.)
), dρк)))
(2.4.)
где ρ1 > ρ2 >… ρк меры на интервале (0, ![]() ), такое, что имеют место равенства
), такое, что имеют место равенства
P1 = P1,0 ![]() P1,1
P1,1 ![]() (
(![]() (
(![]()
![]() Iк ))
(2.5.)
Iк ))
(2.5.)
Р2 = P0,1 ![]() P1,1
P1,1![]() (
(![]()
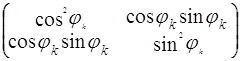
![]() Iк )) (2.6.)
Iк )) (2.6.)
Iк – единичный оператор в L2((0, ![]() ), dρк)
), dρк)
Доказательство. Пространство Н можно представить в виде ортогональной суммы инвариантных подпространств
Н = Н0,0![]() Н0,1
Н0,1![]() Н1,0
Н1,0 ![]() Н1,1
Н1,1 ![]() Н΄, то есть отщепить все одномерные представления от исходного. Н΄ состоит из инвариантных двумерных подпространств.
Н΄, то есть отщепить все одномерные представления от исходного. Н΄ состоит из инвариантных двумерных подпространств.
Всякому положительному функционалу F в *-алгебре P2 отвечает циклическое представление πF *-алгебры P2 в некотором гильбертовом пространстве НF. При этом НF можно реализовать как L2(F), то есть как гильбертово пространство всех функций с интегрируемым квадратом по мере μF на Т.
Пусть каждому вектору ξ![]() Н поставим в соответствие подпространство Нξ
Н поставим в соответствие подпространство Нξ![]() Н, которое получается замыканием множества векторов вида π(х)ξ, где х
Н, которое получается замыканием множества векторов вида π(х)ξ, где х![]() А. Ограничения операторов из π(А) на Нξ является циклическим представлением. Обозначим его через πξ, а соответствующую меру на Т через μξ. Введем упорядочение в Н, полагая ξ>η, если μξ > μη (то есть μη абсолютно непрерывна по мере μξ).
А. Ограничения операторов из π(А) на Нξ является циклическим представлением. Обозначим его через πξ, а соответствующую меру на Т через μξ. Введем упорядочение в Н, полагая ξ>η, если μξ > μη (то есть μη абсолютно непрерывна по мере μξ).
Если η![]() Нξ, то Нη
Нξ, то Нη![]() Нξ, тогда πη – циклическое подпредставление πξ. Пусть Е
Нξ, тогда πη – циклическое подпредставление πξ. Пусть Е![]() Т и μξ (Е) = 0, тогда μη (Е) = 0, следовательно μξ > μη, а значит ξ>η.
Т и μξ (Е) = 0, тогда μη (Е) = 0, следовательно μξ > μη, а значит ξ>η.
Множество максимальных векторов всюду плотно в Н. Пусть существует счетное разложение Н = ![]() Нηк. Пусть {ζi} – последовательность, в которой каждый из векторов ηi встречается бесконечное число раз. Определим ξк индуктивно, так, чтобы выполнялись условия:
Нηк. Пусть {ζi} – последовательность, в которой каждый из векторов ηi встречается бесконечное число раз. Определим ξк индуктивно, так, чтобы выполнялись условия:
1) ξк+1 – максимальный вектор в (![]() Нξi)┴,
Нξi)┴,
2) d (ζк, ![]() Нξi) ≤
Нξi) ≤ ![]() .
.
Тогда разложение Н = ![]() Нξк такое что ξк>ξк+1 и μк>μк+1 .
Нξк такое что ξк>ξк+1 и μк>μк+1 .
Пусть представления πμ в L2(Т, μ) и πν в L2(Т, ν) эквивалентны. Пусть v:L2(Т, μ) →L2(Т, ν) устанавливающий их эквивалентность изоморфизм. Положим f=1, а=v(f), тогда для любой непрерывной функции g на Т v(g)=vπμ(g)f = πν (g)vf = πν (g)a = ga. Так как v – изометрическое отображение, то dμ=|a|2dν. Таким образом мера μ абсолютно непрерывна по мере ν. Аналогично, рассматривая обратный оператор, получаем, что ν абсолютно непрерывна по μ, то есть эти меры эквивалентны. Значит существует разложение Н΄ = ![]() (С2
(С2![]() L2(Т, μк)),
где μ1>μ2>… и соответствующие этим мерам представления неприводимы и неэквивалентны. Это доказывает равенство (2.4.). Тогда из (2.4.) следуют формулы:
L2(Т, μк)),
где μ1>μ2>… и соответствующие этим мерам представления неприводимы и неэквивалентны. Это доказывает равенство (2.4.). Тогда из (2.4.) следуют формулы:
P1 = P1,0 ![]() P1,1
P1,1 ![]() (
(![]() (
(![]()
![]() Iк ))
Iк ))
Р2 = P0,1 ![]() P1,1
P1,1![]() (
(![]()
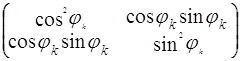
![]() Iк ))
Iк ))
Iк – единичный оператор в L2((0, ![]() ), dρк).
), dρк).
Теорема 2.4. (спектральная теорема в форме разложения единицы). Паре ортопроекторов Р1 и Р2 в сепарабельном гильбертовом пространстве Н соответствует разложение
Н = Н0,0![]() Н0,1
Н0,1![]() Н1,0
Н1,0 ![]() Н1,1
Н1,1![]()
![]() С2
С2![]() Н(φ)dЕ(φ) (2.7.)
Н(φ)dЕ(φ) (2.7.)
в прямой интеграл инвариантных относительно Р1, Р2 подпространств и определенное на Т = (0, ![]() ) разложение dЕ(φ) единичного оператора I+=E(0,
) разложение dЕ(φ) единичного оператора I+=E(0, ![]() ) в Н+ =
) в Н+ =![]() С2
С2![]() Н(φ)dЕ(φ), такое что имеет место равенство
Н(φ)dЕ(φ), такое что имеет место равенство
P1 = P1,0 ![]() P1,1
P1,1 ![]()
![]()
![]() I+
(2.8.)
I+
(2.8.)
Р2 = P0,1 ![]() P1,1
P1,1![]()
![]()
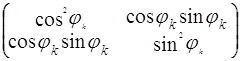
![]() dЕ(φ) (2.9.)
dЕ(φ) (2.9.)
Доказательство. Всякий самосопряженный оператор А, действующий в Н, изометрически изоморфен оператору умножения на независимую переменную в пространстве ![]() L2(R, dρк), где ρк зависит от разложения единицы оператора А. Тогда доказательство спектральной теоремы в форме разложения единицы следует непосредственно из спектральной теоремы в форме операторов умножения.
L2(R, dρк), где ρк зависит от разложения единицы оператора А. Тогда доказательство спектральной теоремы в форме разложения единицы следует непосредственно из спектральной теоремы в форме операторов умножения.
Глава III. Спектр суммы двух ортопроекторов
§1. Спектр суммы двух ортопроекторов в унитарном пространстве
Похожие работы
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...
... для того, чтобы показать школьникам образец современной математической теории. 2.2.3.2. ПРОГРАММА И СОДЕРЖАНИЕ ЗАНЯТИЙ ФАКУЛЬТАТИВНОГО КУРСА «ЭЛЕМЕНТЫ СОВРЕМЕННОЙ АЛГЕБРЫ» В качестве экспериментальной работы мы предлагаем изучение элементов современной алгебры в рамках факультативного курса по математике. Нами была разработана программа факультативного курса «Элементы современной алгебры» и ...
... угодно сложные в логическом отношении схемы, можно строить, используя два приема: 1. последовательное соединение элементов; 2. перестановка входов элементов. Этим двум физическим приемам в алгебре логики соответствуют: 1. принцип суперпозиции (подстановка в функцию вместо ее аргументов других функций); 2. подстановка аргументов (изменение порядка записи аргументов функций или замена ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...

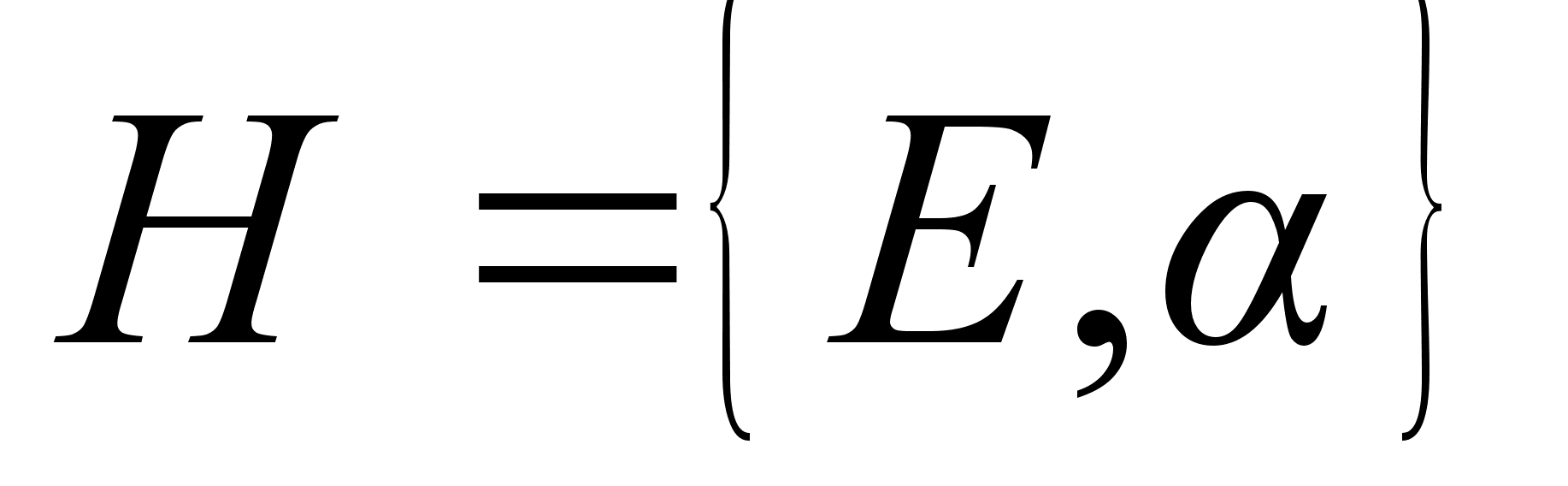
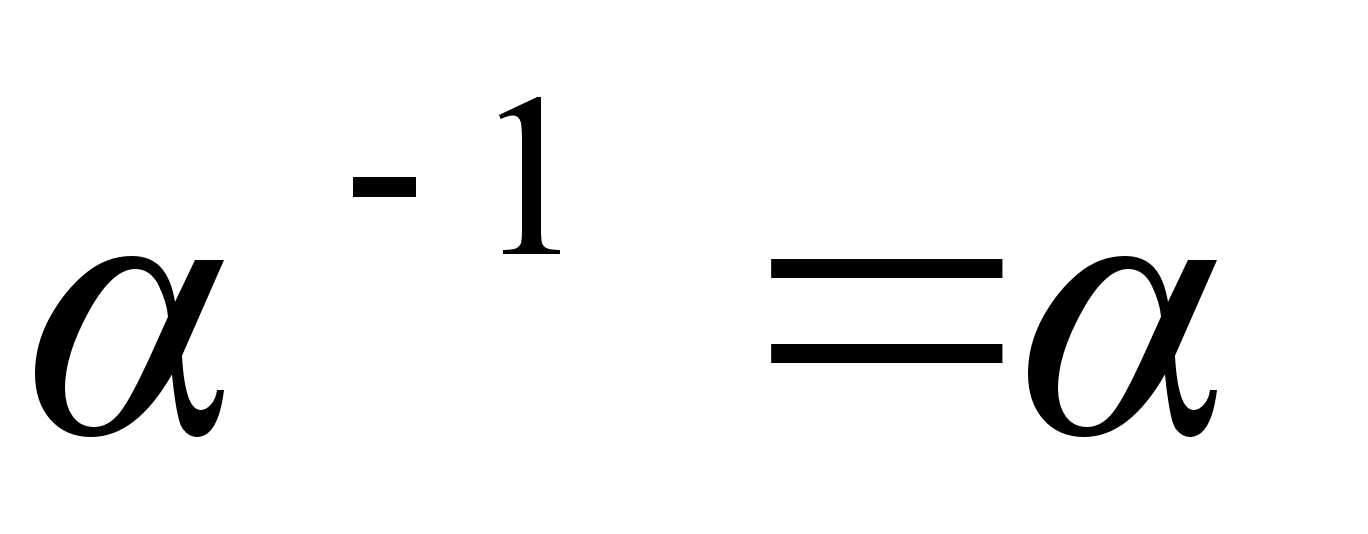
0 комментариев