Навигация
< ε < a
0 < ε < a
Пусть dimH =n. Тогда справедлива теорема.
Теорема 1.3. Самосопряженный оператор А представим в виде линейной комбинации ортопроекоров А = aР1 + bР2, 0<a<b тогда и только тогда, когда
![]() (А)
(А) ![]() {0, a, b, a + b}
{0, a, b, a + b}![]() (
(![]() {εк, a + b - εк}), 0<εк<1, и
{εк, a + b - εк}), 0<εк<1, и
dimНεк = dimНa+b-εк (Нεк , Нa+b-εк - собственные подпространства оператора А, отвечающие εк) к=1,…m.
Доказательство. Пусть А = aР1 + bР2, 0<a<b. Найдем ![]() (А).
(А).
1) х![]() Н0,0, то Ах = 0 и 0
Н0,0, то Ах = 0 и 0![]()
![]() (А);
(А);
2) х![]() Н0,1, то Ах = bx и b
Н0,1, то Ах = bx и b![]()
![]() (А);
(А);
3) х![]() Н1,0, то Ах = ax и a
Н1,0, то Ах = ax и a![]()
![]() (А);
(А);
4) х![]() Н1,1, то Ах = (a+b)x и a+b
Н1,1, то Ах = (a+b)x и a+b![]()
![]() (А).
(А).
Тогда ![]() (А)
(А) ![]() {0, a, b, a + b}
{0, a, b, a + b}![]() (
(![]() {εк , a + b - εк}), где 0<εк<1, к=1,…m. Причем числа εк, a + b - εк входят одновременно в спектр А, и соответству-
{εк , a + b - εк}), где 0<εк<1, к=1,…m. Причем числа εк, a + b - εк входят одновременно в спектр А, и соответству-
ющие собственные подпространства ортогональны и одномерны, так как А=А*. Тогда сумма всех собственных подпространств, отвечающих одному εк также инвариантна относительно А и dimНεк = dimНa+b-εк = qk. (с учетом кратности εк)
Обратно. Существует единственное разложение Н в силу (1.4.)
Н = Н(0)![]() Н(a)
Н(a) ![]() Н(b)
Н(b)![]() Н(a+b)
Н(a+b)![]() (
(![]() (С2
(С2![]() Нк)) (1.9.)
Нк)) (1.9.)
Где Н(0)=Н0,0, Н(a) =Н1,0, Н(b)=Н0,1, Н(a+b)=Н1,1 или
Н = Н(0)![]() Н(a)
Н(a) ![]() Н(b)
Н(b)![]() Н(a+b)
Н(a+b)![]() (
(![]() (Нεк
(Нεк![]() Нa+b-εк) (1.10.)
Нa+b-εк) (1.10.)
Положим
P1 = Pa![]() Pa+b
Pa+b ![]() (
(![]() (
(![]()
![]() Iк ))
(1.11.)
Iк ))
(1.11.)
Р2 = Pb ![]() Pa+b
Pa+b ![]() (
(![]()
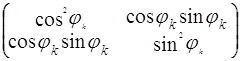
![]() Iк )) (1.12.)
Iк )) (1.12.)
Но тогда
aР1 + bР2 = aPa![]() bPb
bPb ![]() (а+b)Pa+b
(а+b)Pa+b ![]() (a
(a![]() (
(![]()
![]() Iк ))
Iк ))![]()
![]() (b
(b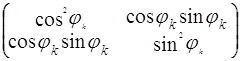
![]() Iк )) = A.
Iк )) = A.
Спектр оператора А совпадает с {0, a, b, a + b}![]() (
(![]() {εк , a + b - εк}), (0<εк<1, к=1,…m) по построению и А = А* как вещественная комбинация ортопроекторов.
{εк , a + b - εк}), (0<εк<1, к=1,…m) по построению и А = А* как вещественная комбинация ортопроекторов.
§ 2. Спектр суммы двух ортопроекторов в сепарабельном гильбертовом пространстве
2.1. Спектр оператора А = Р1 + Р2. Изучим оператор Р1 + Р2 в сепарабельном гильбертовом пространстве.
Теорема 2.1. Самосопряженный оператор А представим в виде суммы двух ортопроекторов А = Р1 + Р2 тогда и только тогда, когда ![]() (А) = [0, 2] и пространство Н можно разложить в ортогональную сумму инвариантных относительно А пространств
(А) = [0, 2] и пространство Н можно разложить в ортогональную сумму инвариантных относительно А пространств
Н = Н0![]() Н1
Н1![]() Н2
Н2 ![]() (
(![]() (С2
(С2![]() L2((0,
L2((0, ![]() ), dρк)))
(2.1.)
), dρк)))
(2.1.)
и меры ρк инвариантны относительно преобразования 1+х → 1-х.
Доказательство. Пусть А = Р1 + Р2.
Н0=Н0,0, Н1=Н1,0![]() Н0,1, Н2=Н1,1
Н0,1, Н2=Н1,1
Поставим в соответствие φ→ε cosφ, где φ![]() (0,
(0, ![]() ). Тогда, как было найдено выше, спектр
). Тогда, как было найдено выше, спектр ![]() (А)
(А) ![]() [0, 2] и Н можно разложить (опираясь на спектральную теореме 2.3. главы II) в ортогональную сумму (2.1.)
[0, 2] и Н можно разложить (опираясь на спектральную теореме 2.3. главы II) в ортогональную сумму (2.1.)
Н = Н0![]() Н1
Н1![]() Н2
Н2 ![]() (
(![]() (С2
(С2![]() L2((0, 2), dρк)))
L2((0, 2), dρк)))
Поскольку собственные подпространства, соответствующие собственным значениям А 1+ε , 1-ε, 0<ε<1 входят одновременно в спектр и их значения совпадают, то каждая мера ρк (к = 1, 2, …) должна быть инвариантной относительно преобразования 1 + х → 1- х.
Обратно. Пусть имеет место (2.1.) и ![]() (А)
(А) ![]() [0, 2]. Тогда зададим ортопроекторы Р1΄ Р2΄ равенствами
[0, 2]. Тогда зададим ортопроекторы Р1΄ Р2΄ равенствами
Р1΄ = P1![]() P2
P2![]() (
(![]() (
(![]()
![]() Iк ))
Iк ))
Р2΄ = P2 ![]() (
(![]()
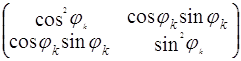
![]() Iк ))
Iк ))
где Pi: Н→Нi (i = 0, 1, 2) ортопроектор, Ik – единичный оператор в L2((0, 2), dρк)). Тогда А =Р1΄ + Р2΄ - самосопряженный оператор, спектр которого содержится в [0, 2], так как Рк΄ (к = 1, 2) является суммой ортопроекторов на взаимно ортогональные пространства.
2.2. Спектр линейной комбинации А = aР1 + bР2 (0<a<b). Рассмотрим теперь случай, когда А = aР1 + bР2 (0<a<b).
Теорема 2.2. Самосопряженный оператор А представим в виде линейной комбинации двух ортопроекторов А = aР1 + bР2, 0<a<b тогда и только тогда, когда ![]() (А)
(А) ![]() [0, a]
[0, a] ![]() [b, a+b] и Н можно представить в виде ортогональной суммы инвариантных относительно А пространств
[b, a+b] и Н можно представить в виде ортогональной суммы инвариантных относительно А пространств
Н = Н0![]() Нa
Нa ![]() Нb
Нb![]() Нa+b
Нa+b![]() (
(![]() (С2
(С2![]() L2([0, a]
L2([0, a] ![]() [b, a+b], dρк)))) (2.2.)
[b, a+b], dρк)))) (2.2.)
и меры ρк инвариантны относительно преобразования х→a+b.
Доказательство. Пусть А = aР1 + bР2 (0<a<b). Пусть Н0=Н0,0, На=Н0,1, Нb=Н1,0, Нa+b=Н1,1. Так как ![]() (А)
(А) ![]() [0, a]
[0, a] ![]() [b, a+b] и собственные подпространства, отвечающие собственным значениям оператора А входят в Н одновременно (причем их размерности совпадают) то аналогично теореме 2.1. получаем
[b, a+b] и собственные подпространства, отвечающие собственным значениям оператора А входят в Н одновременно (причем их размерности совпадают) то аналогично теореме 2.1. получаем
Н = Н0![]() Нa
Нa ![]() Нb
Нb![]() Нa+b
Нa+b![]() (
(![]() (С2
(С2![]() L2([0, a]
L2([0, a] ![]() [b, a+b], dρк))))
[b, a+b], dρк))))
где меры ρк (к = 1, 2, …) инвариантны относительно преобразования х → a+b-х.
Обратно, пусть ![]() (А)
(А) ![]() [0, a]
[0, a] ![]() [b, a+b] и имеется разложение Н (2.2.). Тогда зададим Р1 и Р2
следующим образом
[b, a+b] и имеется разложение Н (2.2.). Тогда зададим Р1 и Р2
следующим образом
P1 = Pa![]() Pa+b
Pa+b ![]() (
(![]() (
(![]()
![]() Iк ))
Iк ))
Р2 = Pb ![]() Pa+b (
Pa+b (![]()
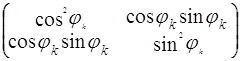
![]() Iк ))
Iк ))
где Рα: Н→Нα , α = a, b, a+b – ортопроекторы, Iк – единичный оператор в L2([0,a] ![]() [b, a+b]). Тогда
[b, a+b]). Тогда
А = aР1 + bР2 = aР1![]() bР2
bР2![]() (a+b)Pa+b
(a+b)Pa+b ![]() (
(![]() (
(![]()
![]() Iк ))
Iк )) ![]()
![]() (
(![]()
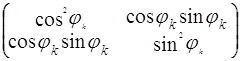
![]() Iк ))
Iк ))
ЗАКЛЮЧЕНИЕ
В дипломной работе изучена пара ортопроекторов в сепарабельном гильбертовом пространстве Н, приведено описание всех неприводимых и неэквивалентные *-представления *-алгебры P2 .
P2 = С <p1, p2 | pк2 = pк* =pк>.
А именно: 4 одномерных π0,0(p1) = 0, π0,0(p2) = 0; π0,1(p1) = 0, π0,1(p2) = 1; π1,0(p1) = 1, π1,0(p2) = 0; π1,1(p1) = 1, π1,1(p2) = 1.
И двумерные: ![]() ,
, 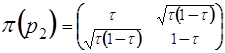 τ
τ![]() (0, 1)
(0, 1)
Изучен спектр операторов Р1 + Р2, aР1 + bР2 (0<a<b), а также необходимые и достаточные условия представимости самосопряженного оператора А в виде А = Р1 + Р2 и А = aР1 + bР2 (0<a<b).
ЛИТЕРАТУРА
1. Ахиезер Н.И., Глазман И.М. Теория линейных операторов в гильбертовом пространстве, М., Наука, 1966.
2. Березенский Ю.М., Ус Г.Ф., Шефтель З.Г. Функциональный анализ, К., Выща школа, 1990.
3. Браттели У., Робинсон Д. Операторные алгебры и квантовая статистическая механика: С*- W* -алгебры. Группы симметрий. Разложение состояний., М., Мир, 1982.
4. Диксмье Ж. С*-алгебры и их представления. М., Наука, 1974.
5. Кириллов А.А. Элементы теории представлений. М., Наука, 1978.
6. Кужель А.В. Алгебры конечного ранга, С. СГУ, 1979.
7. Ленг С. Алгебра. М., Мир, 1968.
8. Мерфи Д. С*-алгебры и теория операторов. М., Мир, 1998.
9. Наймарк М.А. Нормированные кольца. М., Гостехиздат, 1956.
10. Рудин У. Функциональный анализ. М., Мир, 1975.
11. NishioK, Linear algebra and its applications 66: 169-176, Elsevier Science Publishing Co., Inc., 1985.
12. Samoilenko Y.S., Representation theory of algebras, Springer, 1998.
Похожие работы
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...
... для того, чтобы показать школьникам образец современной математической теории. 2.2.3.2. ПРОГРАММА И СОДЕРЖАНИЕ ЗАНЯТИЙ ФАКУЛЬТАТИВНОГО КУРСА «ЭЛЕМЕНТЫ СОВРЕМЕННОЙ АЛГЕБРЫ» В качестве экспериментальной работы мы предлагаем изучение элементов современной алгебры в рамках факультативного курса по математике. Нами была разработана программа факультативного курса «Элементы современной алгебры» и ...
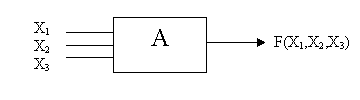
... угодно сложные в логическом отношении схемы, можно строить, используя два приема: 1. последовательное соединение элементов; 2. перестановка входов элементов. Этим двум физическим приемам в алгебре логики соответствуют: 1. принцип суперпозиции (подстановка в функцию вместо ее аргументов других функций); 2. подстановка аргументов (изменение порядка записи аргументов функций или замена ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...

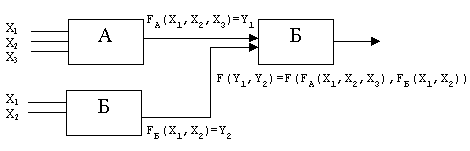
0 комментариев