Навигация
2. Регулярные возмущения.
2.1 Асимптотические методы
Пусть задано банахово пространство 
и отображение 
.
Определение. Будем ряд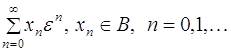 
называть асимптотическим рядом для функции 
, если для любого 
найдутся числа 
и 
такие, что
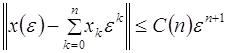при 
(2.1)
Пример 1. Если функция 
имеет производные всех порядков в точке 
, то справедливо формула Тейлора
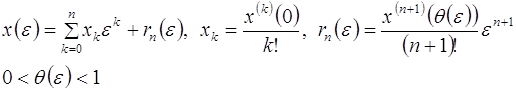(2.2)
Ряд Тейлора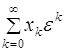 
может расходиться на любом отрезке 
, но он будет асимптотическим рядом для функции . Действительно,
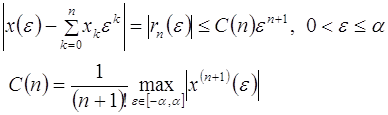(2.3)
Пример 2. Рассмотрим функцию
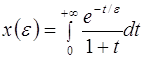
Интегрируя по частям, получаем
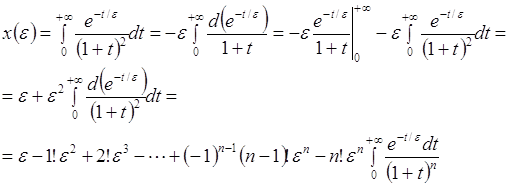
Таким образом,
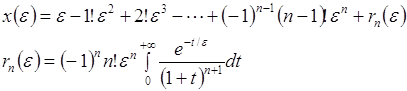
Ряд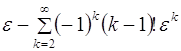 
расходится при любом 
, но является асимптотическим для функции , так как
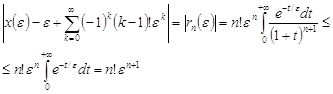
Замечание. Асимптотический ряд может быть полезен при вычислении значений функции при малых или больших значениях параметра.
Рассмотрим функцию примера 2. Вычисляя интеграл численно, получаем при 
Вычисляя частичные суммы асимптотического ряда и оценивая разности 
, получаем первые 20 чисел
0.0015633, -0.0004366, 0.0001633, -0.0000766, 0.0000433, -0.0000287, 0.0000217,
-0.000186, 0.0000177, -0.0000186, 0.00002133, -0.0000266, 0.0000357, -0.0000515,
0.0000793, -0.0001299, 0.0002257, -0.0004145, 0.0008020
Наилучшее приближение дает девятая частичная сумма.
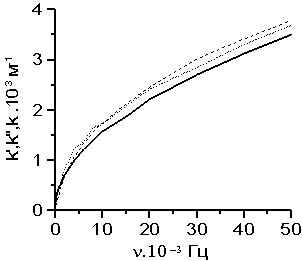
На рис. 1 изображен графически характер приближения частичных сумм к значению. На горизонтали оси откладывается номер , по вертикали частичная сумма 
.
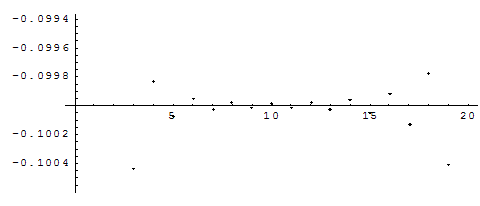
рис. 1
Пусть 
банаховы пространства 
и при 
задано семейство операторов 
. Рассмотрим при 
уравнение 
. Допустим, что это уравнение при каждом 
имеет единственное решение . Уравнение 
будем называть вырожденным. Допустим, что вырожденное уравнение имеет единственное решение 
. Будем говорить, что вырождение регулярное, если
при 
(2.4)
Если (18.4) не выполняется, то говорят, что вырождение сингулярное.
Распространена еще и такая терминология: Уравнение называют уравнением возмущений для уравнения . Если условие (2.4) выполнено, то говорят о регулярных возмущениях. В противном случае речь идет о сингулярных возмущениях. Сам термин «теория возмущений» возник в рамках небесной механики. В следующем параграфе будет исследована задача о регулярных возмущениях для обыкновенных дифференциальных уравнений.
Похожие работы
... . Ван-дер-Поль показал, что для этой цели можно использовать малые нелинейности, однако даже при малых нелинейностях получившаяся задача не допускала интегрирования колебаний в квадратурах. Ван-дер-Поль разработал приближенный асимптотический метод интегрирования дифференциальных уравнений второго порядка подобного рода. 1.1. Метод усреднения Ван-дер-Поля. В своих исследованиях Ван-дер-Поль ...
... Подробное описание различных свойств решений уравнения в связи с их многочисленными приложениями содержится в учебном пособии [8]. Заключение Исследование аналитических свойств решений системы двух нелинейных дифференциальных уравнений третьего порядка, порождаемой прямым и обратным преобразованиями Беклунда высшего аналога второго уравнения Пенлеве позволило доказать существование у неё ...
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
... , момента электромагнитного импульса. Таким образом, имеем серьезную, необходимо требующую разрешения проблему, в которой надо должным образом проанализировать известные либо вскрыть новые реалии в физическом содержании уравнений Максвелла, в частности, понять роль и место векторных потенциалов в явлениях электромагнетизма. Покажем, как это можно сделать! Поставленная задача и проведенный в этом ...
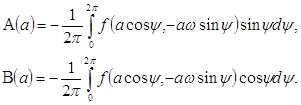
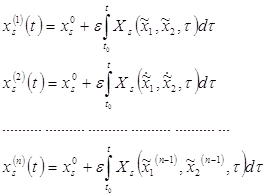
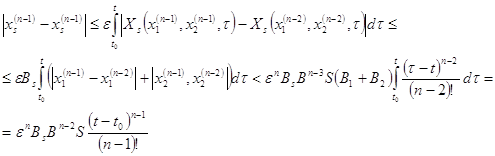
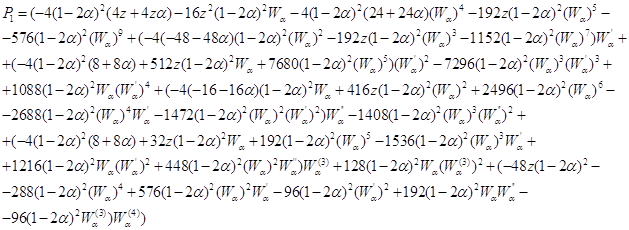
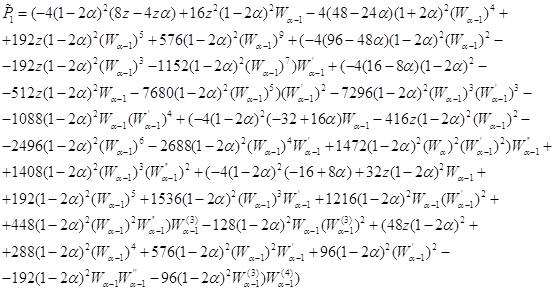
0 комментариев