Регулярные возмущения решений задачи Коши для обыкновенных дифференциальных уравнений

2.2 Регулярные возмущения решений задачи Коши для обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши

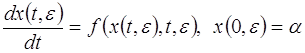(2.2.1)

Функция  непрерывна по переменной  и бесконечно дифференцируемая по переменным  и  при , , .

Предполагается, что вырожденная задача

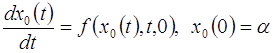(2.2.2)

имеет единственное решение при , причем .

Полагая

(2.2.3)

и воспользовавшись тем, что функция удовлетворяет уравнению (2.2.2) запишем систему уравнений для функции  в виде

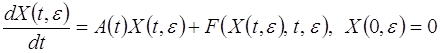(2.2.4)

где

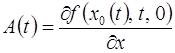(2.2.5)

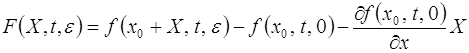(2.2.6)

Будем искать решение задачи Коши (2.1.4) в виде формального ряда по степеням малого параметра

(2.2.7)

Для определения неизвестных функций  получаем рекуррентную систему задач Коши для линейных уравнений (уравнений в вариациях)

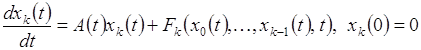(2.2.8)

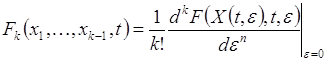
Уравнение (2.2.8) называют уравнением в вариациях.

Вычислим две первых функции

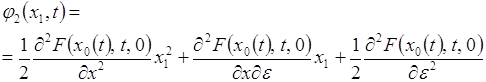 (2.2.9)

Подставляя разложения (2.2.7) и (2.2.8) в уравнения (2.2.4),получаем рекуррентную систему уравнений

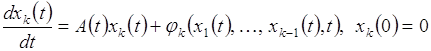(2.2.10)

Все уравнения (2.2.4) имеют одинаковую структуру

, (2.1.11)

Столбцы фундаментальной матрицы  образуют фундаментальную систему решений. При помощи формулы Коши получим решение в виде

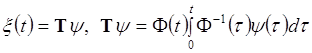(2.2.12)

Линейный оператор  

(2.2.13)

Покажем, что ряд (2.2.3) асимптотический для решения . Положим

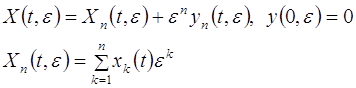(2.2.14)

Применяя формулу Тейлора, получаем

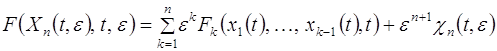(2.2.15)

где функции  те же, что и в формуле (19.8), а

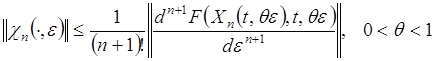(2.2.16)

Подставляя представление (2.2.14) в уравнение (2.2.4), воспользовавшись представлением (2.2.15) и формулами (2.2.8), получаем уравнение для функции .

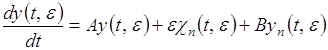(2.2.17)

где

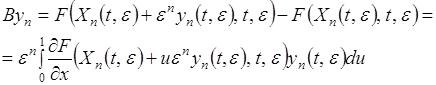(2.2.18)

Из формулы (2.2.6) получаем

и формула (2.2.18) может быть записана в виде

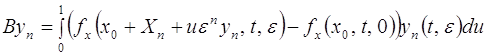 (2.2.19)

Так как вторые производные функции  ограничены, то функция  удовлетворяет условию Липшица и

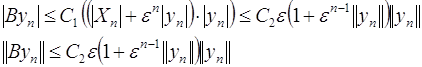(2.2.20)

Вспоминая определение оператора , получаем функциональное уравнение

(2.2.21)

Используя принцип сжатых отображений, покажем, что уравнение (2.1.21) при  имеет единственное решение, и справедливо неравенство . Тем самым будет доказано, что ряд 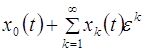   является асимптотическим рядом для функции , являющейся решением задачи Коши (2.2.1).

Пусть . Так как частные производные равномерно непрерывны, то из (2.2.17)- (2.2.20) получаем оценки

при . Таким образом, шар радиуса  отображается в себя при.

Используя (2.2.20), получаем

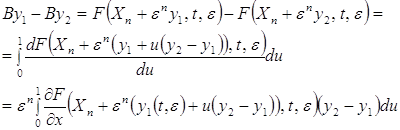
Используя равномерную непрерывность частных производных, получаем

Уменьшая, если нужно,  получаем, что при  оператор  является оператором сжатия. Следовательно,

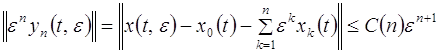
и ряд 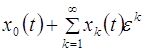асимптотический для решения  задачи Коши (2.1.1).