Навигация
2.3 Метод Леверрьє
Цей метод [1] розкриття вікового визначника заснований на формулах Ньютона для сум степенів коренів алгебраїчного рівняння.
Нехай
![]() (1)
(1)
— характеристичний поліном даної матриці ![]() та
та ![]() — повна сукупність його коренів, де кожен корінь повторюється стільки разів, яка його кратність.
— повна сукупність його коренів, де кожен корінь повторюється стільки разів, яка його кратність.
Покладемо
![]()
![]() .
.
Тоді при ![]() справедливі формули Ньютона
справедливі формули Ньютона
![]()
![]() . (2)
. (2)
Звідси
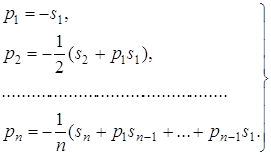 (3)
(3)
Якщо суми ![]() відомі, то за допомогою формул (3) можна крок за кроком визначити коефіцієнти
відомі, то за допомогою формул (3) можна крок за кроком визначити коефіцієнти ![]() характеристичного полінома (1).
характеристичного полінома (1).
Суми ![]() обчислюються таким чином: для
обчислюються таким чином: для ![]() маємо:
маємо:
![]()
Тобто
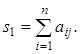 (4)
(4)
Далі, як відомо, ![]() є власними значеннями матриці
є власними значеннями матриці![]() . Тому
. Тому
![]()
тобто якщо
![]()
то
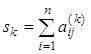 . (5)
. (5)
Степені ![]() знаходяться безпосереднім перемножуванням.
знаходяться безпосереднім перемножуванням.
Таким чином, схема розкриття вікового визначника по методу Леверрьє вельми проста, а саме: спочатку обчислюються ![]() — степені даної матриці А, потім знаходяться відповідні sk - суми елементів головних діагоналей матриць
— степені даної матриці А, потім знаходяться відповідні sk - суми елементів головних діагоналей матриць ![]() , нарешті, по формулах (3) визначаються шукані коефіцієнти
, нарешті, по формулах (3) визначаються шукані коефіцієнти ![]() .
.
Метод Леверрьє вельми трудомісткий, оскільки доводиться підраховувати високі степені даної матриці. Достоїнство його — нескладна схема обчислень і відсутність виняткових випадків.
Приклад. Методом Леверрьє розгорнути характеристичний визначник матриці
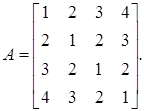
Розв’язання. Утворюємо степені ![]() матриці А. Маємо:
матриці А. Маємо:
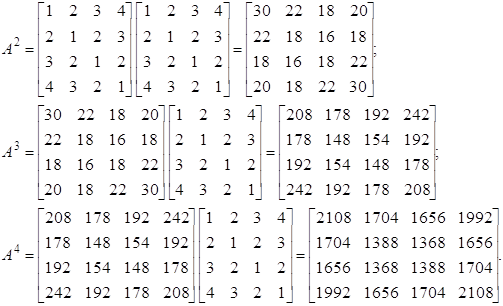
Відмітимо, що не було необхідності обчислювати ![]() повністю, досить було знайти лише головні діагональні елементи цієї матриці.
повністю, досить було знайти лише головні діагональні елементи цієї матриці.
Звідси

Отже, по формулах (3) матимемо:
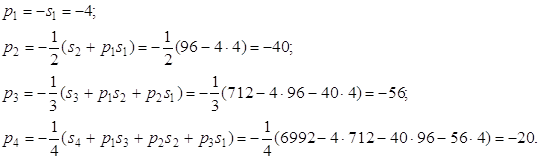
Таким чином, ми одержуємо вже відомий результат:
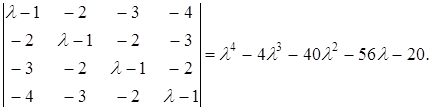
2.4 Метод невизначених коефіцієнтів
Розгортання вікового визначника можна також здійснити за допомогою знаходження досить великої кількості його числових значень.
Нехай
![]() (1)
(1)
є віковим визначником матриці А, тобто
![]() .
.
Якщо в рівності (1) послідовно покласти![]() , то для коефіцієнтів
, то для коефіцієнтів ![]() одержимо систему лінійних рівнянь
одержимо систему лінійних рівнянь
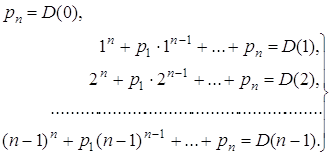 (2)
(2)
Звідси
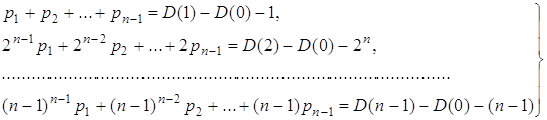 (3)
(3)
І
![]()
З системи (3) можна визначити коефіцієнти ![]() характеристичного полінома (1).
характеристичного полінома (1).
Вводячи матрицю

і вектори
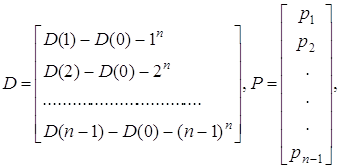
систему (3) можна записати у вигляді матричного рівняння
![]() (4)
(4)
звідси
![]() (5)
(5)
Відмітимо, що обернена матриця ![]() залежить тільки від порядку n вікового визначника і може бути знайдена наперед, якщо доводиться мати справу з масовим розкриттям вікових визначників одного і того ж порядку.
залежить тільки від порядку n вікового визначника і може бути знайдена наперед, якщо доводиться мати справу з масовим розкриттям вікових визначників одного і того ж порядку.
Таким чином, застосування цього методу зводиться до обчислення числових визначників
![]()
![]()
і знаходження розв’язку стандартної лінійної системи (4).
Похожие работы
... і простору матриця лінійного оператора має діагональний вид, то всі вектори базису є власними векторами оператора . Таким чином, доведено наступне твердження. Теорема 5.2. Для того, щоб матриця лінійного оператора у базисі простору була діагональною, необхідно і достатньо, щоб вектори були власними векторами оператора . Теорема 5.3. Якщо власні значення лінійного оператора , діючого в -мі ...
... йний оператор задається матрицею . Отже, при зафіксованому базисі кожному лінійному оператору простору відповідає певна квадратна матриця -го порядку – матриця цього оператора. 3. Власні вектори й власні значення лінійного оператора Означення 1. Підпростір лінійного простору називається інваріантним відносно оператора , якщо , тобто якщо образ будь-якого вектора із міститься в . ...
... і означення Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння. Означення матрець, типи матрець. Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д. Типи матрець: Квадратна матриця, в якої елементи головної діагоналі дорівнюють ...
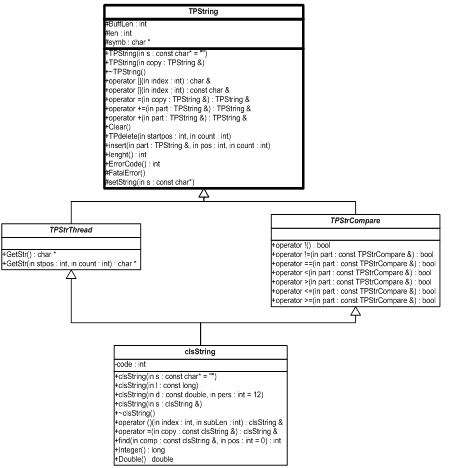
... ліворуч. Перевантажені операції помістити в потік і взяти з потоку повинні об’являтися як дружні, якщо вони повинні мати прямий доступ до закритих елементів класу з міркувань продуктивності. 2. Розробка власного класу clsString 2.1 Загальний алгоритм вирішення Створимо базовий клас TPString у якому розмістимо мінімальнонеобхідні компоненти, але при цьому цей клас вже буде функці ...




0 комментариев