Навигация
Метод А. М. Данілевського
2.1 Метод А. М. Данілевського
Суть методу А. М. Данілевського [1] полягає в приведенні вікового визначника до так званого нормального виду Фробеніуса
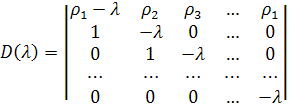 . (1)
. (1)
Якщо нам вдалося записати вікового визначника у формі (1), то, розкладаючи його по елементах першого рядка, матимемо:
![]()
Або
![]() . (2)
. (2)
Таким чином, розгортання вікового визначника, записаного в нормальній формі (1), не представляє труднощів. Позначимо через

дану матрицю, а через
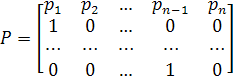
— подібну їй матрицю Фробеніуса, тобто
![]() ,
,
де S - особлива матриця.
Оскільки подібні матриці володіють однаковими характеристичними поліномами, то маємо:
det(A-lE)= det(P-lE). (3)
Тому для обґрунтування методу досить показати, яким чином, виходячи з матриці А, будується матриця Р. Згідно методу А. М. Данілевського, перехід від матриці А до подібної їй матриці Р здійснюється за допомогою т - 1 перетворення подібності, що послідовно перетворюють рядки матриці А, починаючи з останньої, у відповідні рядки матриці Р.
Покажемо початок процесу. Нам необхідно рядок
![]()
перевести в рядок 0 0 ... 1 0. Припускаючи, що ![]() , розділимо всі елементи (n-1) - го стовпця матриці А на
, розділимо всі елементи (n-1) - го стовпця матриці А на ![]() . Тоді її n-й рядок прийме вигляд
. Тоді її n-й рядок прийме вигляд
![]() .
.
Потім віднімемо (n-1) - й стовпець перетвореної матриці, помножений відповідно на числа ![]() , зі всієї решти її стовпців.
, зі всієї решти її стовпців.
В результаті одержимо матрицю, останній рядок якої має бажаний вигляд 0 0 ... 1 0. Вказані операції є елементарними перетвореннями, що здійснюються над стовпцями матриці А. Виконавши ці ж перетворення над одиничною матрицею, одержимо матрицю
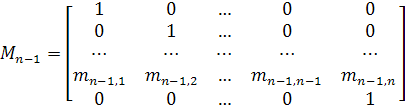
Де
![]() при і ≠ n - 1(4)
при і ≠ n - 1(4)
І
![]() .(4')
.(4')
Звідси робимо висновок, що проведені операції рівносильні множенню справа матриці ![]() на матрицю А, тобто після вказаних перетворень одержимо матрицю
на матрицю А, тобто після вказаних перетворень одержимо матрицю
 . (5)
. (5)
Використовуючи правило множення матриць, знаходимо, що елементи матриці В обчислюються за наступними формулами:
![]() (6)
(6)
![]() (6')
(6')
Проте побудована матриця ![]() не буде подібна матриці А. Для того щоб мати перетворення подібності, потрібно обернену матрицю
не буде подібна матриці А. Для того щоб мати перетворення подібності, потрібно обернену матрицю ![]() зліва помножити на матрицю В:
зліва помножити на матрицю В:
![]() .
.
Безпосередньою перевіркою легко переконатися, що обернена матриця ![]() має вигляд
має вигляд
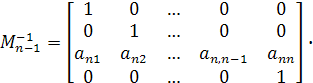 (7)
(7)
Нехай
![]()
Отже
![]() (8)
(8)
Оскільки, очевидно, множення зліва матриці ![]() на матрицю В не змінює перетвореного рядка останньої, то матриця C має вигляд
на матрицю В не змінює перетвореного рядка останньої, то матриця C має вигляд
 (9)
(9)
Перемножуючи матриці ![]() (7) і B (5), матимемо:
(7) і B (5), матимемо:
![]() (10)
(10)
І
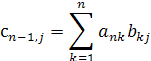
![]() (10')
(10')
Таким чином, множення ![]() на матрицю В змінює лише (n - 1) -й рядок матриці В. Елементи цього рядка знаходяться за формулами (10) і (10'). Одержана матриця C подібна матриці А і має один зведений рядок. Цим закінчується перший етап процесу.
на матрицю В змінює лише (n - 1) -й рядок матриці В. Елементи цього рядка знаходяться за формулами (10) і (10'). Одержана матриця C подібна матриці А і має один зведений рядок. Цим закінчується перший етап процесу.
Далі, якщо ![]() , то над матрицею C можна повторити аналогічні операції, узявши за основу (n - 2) -й її рядок. В результаті одержимо матрицю
, то над матрицею C можна повторити аналогічні операції, узявши за основу (n - 2) -й її рядок. В результаті одержимо матрицю
![]()
з двома зведеними рядками. Над останньою матрицею проробляємо ті ж операції. Продовжуючи цей процес, ми, нарешті, одержимо матрицю Фробеніуса
![]()
якщо, звичайно, всі n - 1 проміжних перетворень можливі. Весь процес може бути оформлений в зручну обчислювальну схему, складання якої покажемо на наступному прикладі.
Приклад. Привести до вигляду Фробеніуса матрицю
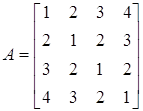 .
.
Розв’язання.
Обчислення розташовуємо в таблицю 1.
| Номер рядка |
| Рядки матриці | Σ | Σ’ | |||
| 1 | 2 | 3 | 4 | ||||
| 1 2 3 4 | 1 2 3 4 | 2 1 2 3 | 3 2 1 2 | 4 3 2 1 | 10 8 8 10 | ||
| І |
| –2 | –1,5 | 0,5–1 | –0,5 | –5 | |
| 5 6 7 8 | 4 3 2 1 | –5 2 1 0 | –2,5 –2 0,5 0 | 1,5 1 0,5 1 | 2,5 2 1,5 0 | –3,5 –1 3,5 1 | –5 –2 3 0 |
| 7’ | –24 | –15 | 11 | 19 | –9 | ||
| ІІ |
| –1,600 | –0,067 –1 | 0,733 | 1,267 | –0,600 | |
| 9 | –24 | –1 | 0,167 | –0,333 | –0,667 | –1,833 | –2 |
| 10 | –15 | 1,2 | 0,133 | –0,467 | –0,533 | 0,333 | 0,2 |
| 11 | 11 | 0 | 1 | 0 | 0 | 1 | 0 |
| 12 | 19 | 0 | 0 | 1 | 0 | 1 | 1 |
| 10’ | 6 | 5 | 34 | 24 | 69 | ||
| ІІІ |
| 0,167–1 | –0,833 | –5,667 | –4,000 | –11,500 | |
| 13 | 6 | –0,167 | 1 | 5,333 | 3,333 | 9,500 | 9,667 |
| 14 | 5 | 1 | 0 | 0 | 0 | 1 | 0 |
| 15 | 34 | 0 | 1 | 0 | 0 | 1 | 1 |
| 16 | 24 | 0 | 0 | 1 | 0 | 1 | 1 |
| 13’ | 4 | 40 | 56 | 20 | 120 | ||
У рядках 1-4 таблиці 1 розміщуємо елементи ![]() даної матриці і контрольні суми
даної матриці і контрольні суми  . Відзначаємо елемент
. Відзначаємо елемент ![]() , що належить третьому стовпцю (відмічений стовпець). У рядку 1 записуємо елементи третього рядка матриці
, що належить третьому стовпцю (відмічений стовпець). У рядку 1 записуємо елементи третього рядка матриці ![]() , що обчислюються за формулами (4) і (4'):
, що обчислюються за формулами (4) і (4'):

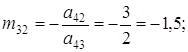
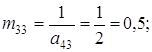

Сюди ж (рядок 1 таблиці 1) поміщаємо елемент
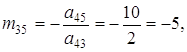
що одержується аналогічним прийомом з контрольного стовпця Σ. Число -5 повинно співпасти з сумою елементів рядка I, що не входять в контрольний стовпець (після заміни елементу ![]() на -1). Для зручності число -1 записуємо поряд з елементом
на -1). Для зручності число -1 записуємо поряд з елементом ![]() , відокремлюючи від останнього межею.
, відокремлюючи від останнього межею.
У рядках 5-8 в графі М-1 виписуємо третій рядок матриці М-1, яка в силу формули (7) співпадає з четвертим рядком початкової матриці А. У рядках 5-8 у відповідних стовпцях виписуємо елементи матриці
B = АМ3,
що обчислюються за двочленними формулами (6) для невідмічених стовпців і по одночленній формулі (6') для відміченого стовпця. Наприклад, для першого стовпця маємо:

і т.д.
Перетворені елементи третього (відміченого) стовпця отримуються за допомогою множення початкових елементів на ![]() = 0,5. Наприклад,
= 0,5. Наприклад,

Відмітимо, що останній рядок матриці В повинен мати вигляд
0 0 1 0.
Для контролю поповнюємо матрицю В перетвореними по аналогічних двочленних формулах з ![]() відповідними елементами стовпця Σ. Наприклад,
відповідними елементами стовпця Σ. Наприклад,
![]()
![]()
![]()
![]()
Отримані результати записуємо в стовпці Σ' у відповідних рядках. Додавши до них елементи третього стовпця, одержимо контрольні суми
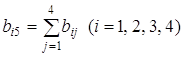
для рядків 5-8 (стовпець Σ).
Перетворення ![]() ,що проведене над матрицею і що дає матрицю
,що проведене над матрицею і що дає матрицю ![]() , змінює лише третій рядок матриці В, тобто сьомий рядок таблиці. Елементи цього перетвореного рядка 7' виходять по формулі (10), тобто є сумами парних добутків елементів стовпця
, змінює лише третій рядок матриці В, тобто сьомий рядок таблиці. Елементи цього перетвореного рядка 7' виходять по формулі (10), тобто є сумами парних добутків елементів стовпця ![]() , що знаходяться в рядках 5-8, на відповідні елементи кожного із стовпців матриці В. Наприклад
, що знаходяться в рядках 5-8, на відповідні елементи кожного із стовпців матриці В. Наприклад
![]()
і т. д.
Такі ж перетворення проводимо над стовпцем Σ:
![]()
В результаті одержуємо матрицю C, що складається з рядків 5, 6, 7', 8 з контрольними сумами Σ, причому матриця C подібна матриці А і має один зведений рядок 8. Цим закінчується побудова першого подібного перетворення ![]() .
.
Далі, прийнявши матрицю C за вихідну і виділивши елемент ![]() (другий стовпець), продовжуємо процес аналогічним чином. В результаті одержуємо матрицю
(другий стовпець), продовжуємо процес аналогічним чином. В результаті одержуємо матрицю ![]() , елементи якої розташовані в рядках 9, 10', 11, 12, що містить два зведені рядки. Нарешті, відправляючись від елементу
, елементи якої розташовані в рядках 9, 10', 11, 12, що містить два зведені рядки. Нарешті, відправляючись від елементу ![]() (перший стовпець) і перетворюючи матрицю D в подібну їй, одержуємо шукану матрицю Фробеніуса Р, елементи якої записані в рядках 13', 14, 15, 16. На кожному етапі процесу контроль здійснюється за допомогою стовпців Σ і Σ'.
(перший стовпець) і перетворюючи матрицю D в подібну їй, одержуємо шукану матрицю Фробеніуса Р, елементи якої записані в рядках 13', 14, 15, 16. На кожному етапі процесу контроль здійснюється за допомогою стовпців Σ і Σ'.
Таким чином, матриця Фробеніуса буде мати вигляд:
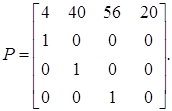
Звідси віковий визначник, приведений до нормального виду Фробеніуса, запишеться так:
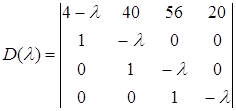
або
![]() .
.
Виняткові випадки в методі А. М. Данілевського.
Процес А. М. Данілевського [1] відбувається без жодних ускладнень, якщо всі елементи, що виділяються, відмінні від нуля. Ми зупинимося зараз на виняткових випадках, коли ця вимога порушується.
Припустимо, що при перетворенні матриці А в матрицю Фробеніуса Р ми після декількох кроків пришли до матриці вигляду
 ,
,
причому виявилось, що ![]() .
.
Тоді продовжувати перетворення по методу А. М. Данілевського не можна. Тут можливі два випадки.
1. Нехай якийсь елемент матриці D, що стоїть ліворуч нульового елемента ![]() , відмінний від нуля, тобто
, відмінний від нуля, тобто ![]() , де
, де![]() . Тоді цей елемент висуваємо на місце нульового елементу
. Тоді цей елемент висуваємо на місце нульового елементу ![]() , тобто переставляємо (k-1) -й і k -й стовпці матриці D і одночасно переставляємо її (k-1) -й і l-й рядки. Можна довести, що одержана нова матриця D' буде подібна колишній. До нової матриці застосовуємо метод А.М.Данілевського.
, тобто переставляємо (k-1) -й і k -й стовпці матриці D і одночасно переставляємо її (k-1) -й і l-й рядки. Можна довести, що одержана нова матриця D' буде подібна колишній. До нової матриці застосовуємо метод А.М.Данілевського.
2. Нехай ![]() , тоді D має вигляд
, тоді D має вигляд
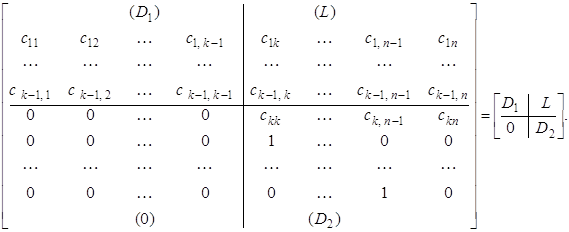
У такому разі віковий визначник det(D - lЕ) розпадається на два визначники
det (D - lЕ) = det (D1 - lЕ) det (D2 - lЕ).
При цьому матриця D2 вже приведена до канонічної форми Фробеніуса і тому det (D2 - lЕ) обчислюється відразу. Залишається застосувати метод А. М. Данілевського до матриці D1.
Обчислення власних векторів по методу А. М. Данілевського.
Метод А. М. Данілевського [1] дає можливість визначати власні вектори даної матриці А, якщо відомі її власні значення. Неай l — власне значення матриці А, а отже, і власне значення подібної їй матриці Фробеніуса Р.
Знайдемо власний вектор ![]() матриці Р, відповідний даному значенню l: Ру = lу. Звідси (Р - lЕ) у = 0 або
матриці Р, відповідний даному значенню l: Ру = lу. Звідси (Р - lЕ) у = 0 або
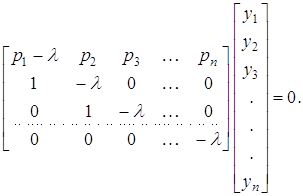
![]()
![]()
![]()
Перемножуючи матриці, одержимо систему для визначення координат ![]() власного вектора у:
власного вектора у:
 (1)
(1)
Система (1) — однорідна. З точністю до коефіцієнта пропорційності розв’язки її можуть бути знайдені таким чином. Покладемо yn=1. Тоді послідовно одержимо:
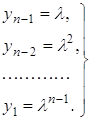 (2)
(2)
Таким чином, шуканий власний вектор є
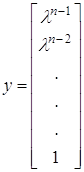 .
.
Позначимо тепер через х власний вектор матриці А, що відповідає значенню l. Тоді, очевидно, маємо:
![]() .
.
Перетворення M1, здійснене над y, дає:
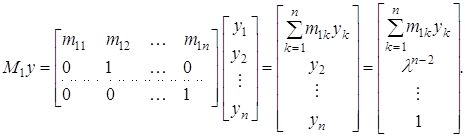
Таким чином, перетворення М1 змінює лише першу координату вектора. Аналогічно перетворення М2 змінить лише другу координату вектора М1у і т.д. Повторивши цей процес n-1 разів, одержимо шуканий власний вектор х матриці А.
Похожие работы
... і простору матриця лінійного оператора має діагональний вид, то всі вектори базису є власними векторами оператора . Таким чином, доведено наступне твердження. Теорема 5.2. Для того, щоб матриця лінійного оператора у базисі простору була діагональною, необхідно і достатньо, щоб вектори були власними векторами оператора . Теорема 5.3. Якщо власні значення лінійного оператора , діючого в -мі ...
... йний оператор задається матрицею . Отже, при зафіксованому базисі кожному лінійному оператору простору відповідає певна квадратна матриця -го порядку – матриця цього оператора. 3. Власні вектори й власні значення лінійного оператора Означення 1. Підпростір лінійного простору називається інваріантним відносно оператора , якщо , тобто якщо образ будь-якого вектора із міститься в . ...
... і означення Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння. Означення матрець, типи матрець. Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д. Типи матрець: Квадратна матриця, в якої елементи головної діагоналі дорівнюють ...
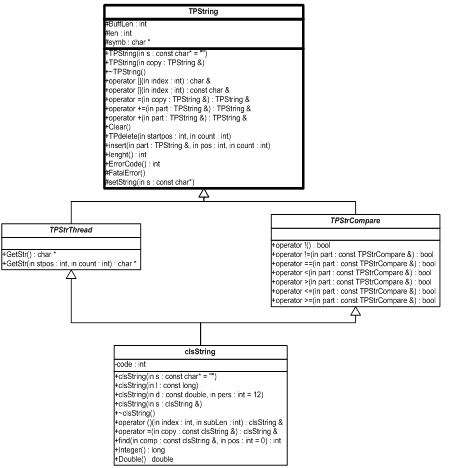
... ліворуч. Перевантажені операції помістити в потік і взяти з потоку повинні об’являтися як дружні, якщо вони повинні мати прямий доступ до закритих елементів класу з міркувань продуктивності. 2. Розробка власного класу clsString 2.1 Загальний алгоритм вирішення Створимо базовий клас TPString у якому розмістимо мінімальнонеобхідні компоненти, але при цьому цей клас вже буде функці ...




0 комментариев