Навигация
Приклади задач, що зводяться до відшукання власних значень та власних векторів матриці
37560
знаков
25
таблиц
38
изображений
2.6 приклади задач, що зводяться до відшукання власних значень та власних векторів матриці
Задача 1
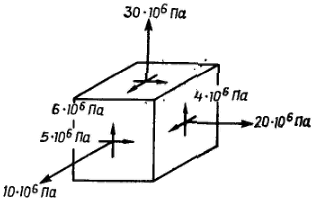
Дослідимо тривісне напруження стану елемента тіла, представленого на малюнку. Матриця напруги для нього має вигляд
Якщо виходити з того, що руйнування станеться при максимальній напрузі, то необхідно знати величину найбільшого головного напруження яке відповідає найбільшому власному значенню матриці напруги. Для знаходження цієї напруги скористаємося одним методом ітерацій. Одержимо власне значення 
і такий власний вектор 
Задача 2. [12, стор. 70]Для довільного тривимірного твердого тіла можна ввести три моменти інерції відносно трьох взаємно перпендикулярних осей і три змішані моменти інерції відносно трьох координатних площин. Відомо, що для несиметричного тіла при фіксованому початку координат існує єдина орієнтація координатних осей, при якій змішані моменти інерції обертаються в нуль. Такі осі називаються головними осями інерції, а відповідні моменти інерції - головними моментами інерції, серед яких є найбільший, найменший і такий, що має проміжне значення. Для матриці моментів інерції
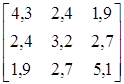
знайти три головних моменти інерції.
Задача 3. [12, стор. 70]Баржа призначена для перевезення через озеро Ері зчепки з шести залізничних вагонів. Буксир тягне її за носову частину, як показано на малюнку. Значення мас вагонів і коефіцієнтів жорсткості сполучних елементів вказані під малюнком. Існує побоювання, що в зчепленні вагонів при хвилюванні на озері можуть виникнути резонансні продольні коливання. Обчислити шість власних частот даної механічної системи і порівняти їх з частотою хвилі, рівній 1 рад/с. Власні частоти пов'язані з власними значеннями динамічної матриці D співвідношенням
Динамічна матриця утворюється із матриць жорсткості [К] і мас [M]
.
Задача 4. [12, стор. 71] Консольний брус довжиною 10 м, що має згинну жорсткість 
і погону масу 10 кг/м, апроксимується двома точковими масами по 50 кг кожна, що розташовані в центрі та на вільному кінці бруса.
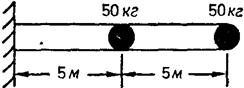
Потрібно знайти дві основні частоти коливань бруса. Це можна зробити, знаючи власні значення 
динамічної матриці 
та маючи на увазі, що
.
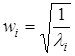— діагональна матриця, на діагоналі якої стоять маси точок;
— матриця згину, в якій елементи і-го рядка являють собою відхилення точки j під дією одиничної сили, що прикладена до точки і. Осьова сила відсутня. Деформаціями здвигу можна знехтувати.
Висновки
У першому розділі курсової роботи проаналізовано науково-методичну літературу з теми дослідження.
Вивчення даної теми ми почали з розкриття дуже важливого для нашого дослідження поняття "матриця".
Ми розглянули основні відомості про матриці та визначники, висвітлили означення власних значень та власних векторів матриць.
В другому розділі ми розглянули теоретичні основи таких методів:
1) метод А. М. Данілевського;
2) метод А. Н. Крилова;
3) метод Леверрьє;
4) метод невизначених коефіцієнтів;
5) метод скалярних добутків для знаходження першого власного значення дійсної матриці.
Наведені приклади задач з фізики, що зводяться до відшукання власних значень та власних векторів матриці.
Дана робота має практичне застосування, її матеріал може бути використаний на факультативних заняттях з лінійної алгебри для формування наукового світогляду та математичної культури студентів.
Список використаних джерел
1. Демидович Б. П., Марон И. А. Основы вычислительной математики. — 3-е изд. — М.: Наука, 1966. — 560 с.
2. Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб. Для вузов — 4-е изд. — М.: Наука. Физматлит, 1999. — 296 с.
3. Калиткин Н. Н. Численные методы. — М.: Мир, 1988. — 512 с.
4. Мальцев А. И. Основы линейной алгебры. — 3-е изд. — М.: Наука, 1968. — 402 с.
5. Марчук Г. И. Методы вычислительной математики — М.: Наука, 1977. — 392с., ил.
6. Приближение функций, дифференциальные и интегральные уравнения/Под ред. Б. П. Демидовича. — М.: Наука, 1987. — 368 с.
7. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. — М.: Физматгиз, 1963. — 408 с.
8. Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на производстве: Пер. с англ. — М.: Мир, 1982. — 304 с., ил.
9. Форсайт Дж., Молер К. Численное решение систем линейных уравнений. — М.: Мир, 1969. — 285 с.
10. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений: Пер. с англ. — М.: Мир, 1980. — 277 с., ил.
11. Хемминг Р. В. Цыфровые фильтры: Пер. с англ./Под ред. А. М. Трахтмана — М.: Советское радио, 1980. — 224 с., ил.
12. Шуп Т. Решение инженерных задач на ЭВМ: Практическое руководство. Пер. с англ. — М.: Мир, 1982. — 238с., ил.
[1] Нормуванням (на одиницю) вектора х називають множення його на ; нормований вектор має одиничну довжину.
Похожие работы
... і простору матриця лінійного оператора має діагональний вид, то всі вектори базису є власними векторами оператора . Таким чином, доведено наступне твердження. Теорема 5.2. Для того, щоб матриця лінійного оператора у базисі простору була діагональною, необхідно і достатньо, щоб вектори були власними векторами оператора . Теорема 5.3. Якщо власні значення лінійного оператора , діючого в -мі ...
... йний оператор задається матрицею . Отже, при зафіксованому базисі кожному лінійному оператору простору відповідає певна квадратна матриця -го порядку – матриця цього оператора. 3. Власні вектори й власні значення лінійного оператора Означення 1. Підпростір лінійного простору називається інваріантним відносно оператора , якщо , тобто якщо образ будь-якого вектора із міститься в . ...
... і означення Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння. Означення матрець, типи матрець. Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д. Типи матрець: Квадратна матриця, в якої елементи головної діагоналі дорівнюють ...
... ліворуч. Перевантажені операції помістити в потік і взяти з потоку повинні об’являтися як дружні, якщо вони повинні мати прямий доступ до закритих елементів класу з міркувань продуктивності. 2. Розробка власного класу clsString 2.1 Загальний алгоритм вирішення Створимо базовий клас TPString у якому розмістимо мінімальнонеобхідні компоненти, але при цьому цей клас вже буде функці ...
0 комментариев