Навигация
Метод скалярних добутків для знаходження першого власного значення дійсної матриці
2.5 Метод скалярних добутків для знаходження першого власного значення дійсної матриці
Для відшукання першого власного значення ![]() дійсної матриці А можна вказати дещо інший ітераційний процес, що є іноді вигіднішим. Метод [1] заснований на утворенні скалярних добутків
дійсної матриці А можна вказати дещо інший ітераційний процес, що є іноді вигіднішим. Метод [1] заснований на утворенні скалярних добутків
![]() і
і ![]()
![]() де А' — матриця, транспонована з матрицею А, і у0 — вибраний яким-небудь чином початковий вектор.
де А' — матриця, транспонована з матрицею А, і у0 — вибраний яким-небудь чином початковий вектор.
Переходимо тепер до викладу самого методу.
Нехай А — дійсна матриця і ![]() — її власні значення, які передбачаються різними, причому
— її власні значення, які передбачаються різними, причому
![]()
Візьмемо деякий ненульовий вектор у0 і за допомогою матриці А побудуємо послідовність ітерацій
|
| (1) |
Для вектора у0 утворюємо також за допомогою транспонованої матриці А' другу послідовність ітерацій
|
| (2) |
де ![]() .
.
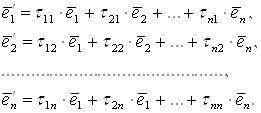
Згідно з теоремою 1 розділу X § 16 в просторі Еп виберемо два власні базиси ![]() і
і ![]() відповідно для матриць А і А', що задовольняють умовам біортонормування:
відповідно для матриць А і А', що задовольняють умовам біортонормування:
|
| (3) |
де ![]() і
і ![]() . Позначимо координати вектора у0 в базисі
. Позначимо координати вектора у0 в базисі ![]() через
через ![]() , а в базисі
, а в базисі ![]() — через
— через ![]() тобто
тобто
![]() і
і ![]()
Звідси
|
| (4) |
І
|
| ( |
Складемо скалярний добуток
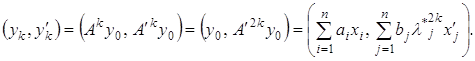
Звідси через умову ортонормування знаходимо:
|
| (5) |
Аналогічно
|
| (6) |
Отже, при ![]() маємо:
маємо:
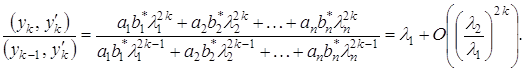
Таким чином,
|
| (7) |
Цей метод особливо зручний для симетричної матриці А, оскільки тоді А'=А, і ми маємо просто
|
| (8) |
і, отже, тут потрібно побудувати тільки одну послідовність ![]() .
.
Приклад. Методом скалярних добутків знайти найбільше власне значення матриці
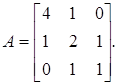
Розв’язання. Оскільки матриця А — симетрична, то досить побудувати лише одну послідовність ітерацій ![]() .
.
Вибираючи за початковий вектор

можна використати результати таблиці 27. Наприклад, при k = 5 і k = 6 маємо:
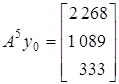 і
і 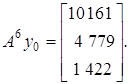
![]()
Звідси
![]()
І ![]()
Отже,
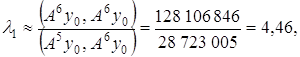
що співпадає в написаних знаках із значенням, знайденим раніше за допомогою А10у0.
Зауваження. Методи знаходження найбільшого по модулю кореня характеристичного рівняння можна використовувати для знаходження найбільшого по модулю кореня алгебраїчного рівняння
|
| (9) |
Дійсно, рівняння (9), як легко безпосередньо перевірити, є віковим для матриці
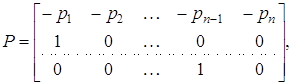
тобто рівняння (9) еквівалентно рівнянню
![]()
Якщо рівняння (9) не має нульового кореня, то аналогічним способом може бути визначений найменший по модулю корінь цього рівняння, а саме, при ![]() ,вважаючи
,вважаючи ![]() , одержимо:
, одержимо:
|
| (10) |
Зворотна величина найбільшого по модулю кореня рівняння (10), очевидно, дасть нам найменший по модулю корінь рівняння (9).
Знаходження другого власного значення матриці і другого власного вектора.
Нехай власні значення ![]() матриці А такі, що
матриці А такі, що
|
| (1) |
тобто є два відмінних один від одного, найбільших по модулю власних значення ![]() і
і ![]() матриці А. У такому разі прийомом, аналогічним розібраному вище (§ 11), можна приблизно знайти друге власне значення
матриці А. У такому разі прийомом, аналогічним розібраному вище (§ 11), можна приблизно знайти друге власне значення ![]() і власний вектор
і власний вектор ![]() , що відповідає йому.
, що відповідає йому.
З формули (2) маємо:
|
| (2) |
І
|
| (3) |
Виключимо з формул (2) і (3) члени, що містять ![]() . Для цього від рівності (3) віднімемо рівність (2), помножену на
. Для цього від рівності (3) віднімемо рівність (2), помножену на ![]() . В результаті одержимо:
. В результаті одержимо:
|
| (4) |
Введемо позначення
|
| (5) |
причому вираз (5) називатимемо ![]() - різницею від
- різницею від ![]() . Якщо
. Якщо ![]() , то очевидно, що перший доданок в правій частині рівності (4) є її головним членом при
, то очевидно, що перший доданок в правій частині рівності (4) є її головним членом при ![]() , і ми маємо наближену рівність
, і ми маємо наближену рівність
|
| (6) |
Звідси
|
| (7) |
Нехай

З формул (6) і (7) виводимо:
|
| (8) |
Користуючись формулою (8), можна приблизно обчислити друге власне значення ![]() . Відмітимо, що на практиці зважаючи на втрату точності при відніманні близьких чисел іноді вигідніше номер ітерації k для визначення
. Відмітимо, що на практиці зважаючи на втрату точності при відніманні близьких чисел іноді вигідніше номер ітерації k для визначення ![]() брати меншим, ніж номер ітерації т для визначення
брати меншим, ніж номер ітерації т для визначення ![]() , тобто доцільно вважати:
, тобто доцільно вважати:
|
| (9) |
де k- найменше з чисел, при якому починає позначатися переважання ![]() над наступними власними значеннями. Формула (9), взагалі кажучи, дає грубі значення для
над наступними власними значеннями. Формула (9), взагалі кажучи, дає грубі значення для ![]() . Відмітимо, що якщо модулі всіх власних значень різні між собою, то за допомогою формул, аналогічних формулі (9), можна обчислити і решту власних значень даної матриці. Проте результати обчислень будуть ще менш надійні.
. Відмітимо, що якщо модулі всіх власних значень різні між собою, то за допомогою формул, аналогічних формулі (9), можна обчислити і решту власних значень даної матриці. Проте результати обчислень будуть ще менш надійні.
Що стосується власного вектора ![]() , те, як витікає з формули (6), можна покласти:
, те, як витікає з формули (6), можна покласти:
|
| (10) |
Є розповсюдження даного методу на випадок кратного кореня характеристичного рівняння.
Приклад. Визначити подальші власні значення і власні вектори матриці

Розв’язання. Для знаходження другого власного значення приймемо k = 8. Маємо:
|
|
|
|
| 45433 21141 6 201 | 202833 93906 27 342 | 905238 417987 121 248 |
Складаємо ![]() - різниці по формулі
- різниці по формулі
![]()
де ![]() . Для кожного із стовпців приймається своє значення
. Для кожного із стовпців приймається своє значення ![]() а саме:
а саме: ![]() = 4,462;
= 4,462; ![]() = 4,456;
= 4,456; ![]() = 4,447 (таблиця 2).
= 4,447 (таблиця 2).
Таблиця 2
Обчислення другого власного значення
|
|
|
|
|
|
|
| 202833 93906 27 342 | 202722 94204 27 76 | 111 – 298 – 234 | 905238 417987 121 248 | 905041 418445 121 590 | 197 – 458 – 342 |
Звідси одержуємо:
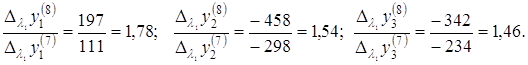
Отже, приблизно можна прийняти:
![]()
В якості другого власного вектора можна прийняти:
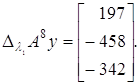
Нормуючи цей вектор, одержимо:
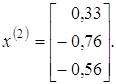
Оскільки матриця А — симетрична, то вектори ![]() і
і ![]() повинні бути ортогональні між собою. Перевірка дає:
повинні бути ортогональні між собою. Перевірка дає:
![]()
Звідси ![]() , що досить неточно.
, що досить неточно.
Третє власне значення ![]() знаходимо по сліду матриці А:
знаходимо по сліду матриці А:
![]()
Звідси
![]() .
.
Власний вектор
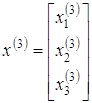
можна обчислити з умов ортогональності:
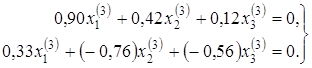
Звідси
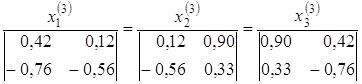
Або
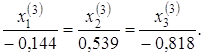
Після нормування остаточно отримаємо:
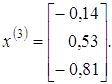
Похожие работы
... і простору матриця лінійного оператора має діагональний вид, то всі вектори базису є власними векторами оператора . Таким чином, доведено наступне твердження. Теорема 5.2. Для того, щоб матриця лінійного оператора у базисі простору була діагональною, необхідно і достатньо, щоб вектори були власними векторами оператора . Теорема 5.3. Якщо власні значення лінійного оператора , діючого в -мі ...
... йний оператор задається матрицею . Отже, при зафіксованому базисі кожному лінійному оператору простору відповідає певна квадратна матриця -го порядку – матриця цього оператора. 3. Власні вектори й власні значення лінійного оператора Означення 1. Підпростір лінійного простору називається інваріантним відносно оператора , якщо , тобто якщо образ будь-якого вектора із міститься в . ...
... і означення Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння. Означення матрець, типи матрець. Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д. Типи матрець: Квадратна матриця, в якої елементи головної діагоналі дорівнюють ...
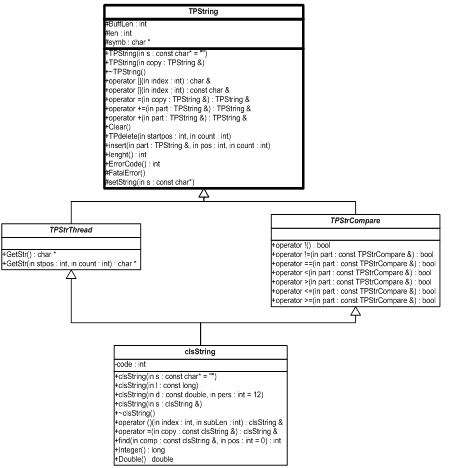
... ліворуч. Перевантажені операції помістити в потік і взяти з потоку повинні об’являтися як дружні, якщо вони повинні мати прямий доступ до закритих елементів класу з міркувань продуктивності. 2. Розробка власного класу clsString 2.1 Загальний алгоритм вирішення Створимо базовий клас TPString у якому розмістимо мінімальнонеобхідні компоненти, але при цьому цей клас вже буде функці ...
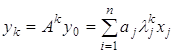

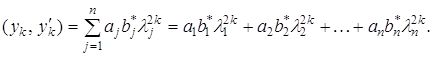
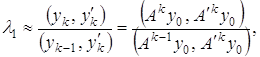
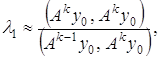
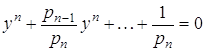
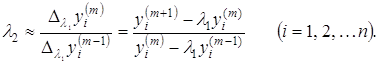
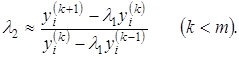




0 комментариев