Навигация
4. Вычитание (разность)
Разность множеств А и В есть множество С, элементы которого обладают свойствами множества А и не обладают свойствами множества В или принадлежат множеству А и не принадлежат множеству В.
![]()
5. Дополнение
Если имеется некоторое универсальное множество (универсум) U и все рассматриваемые множества есть его подмножества, то дополнением ![]() называется такое множество, элементы которого не входят в А, но принадлежат U.
называется такое множество, элементы которого не входят в А, но принадлежат U.
(Диаграммы Эймера, Венна)
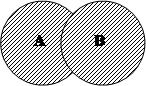 1.
1.
![]()

2.
![]()
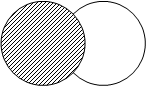
|
|
![]()

|
 4.
4. ![]()
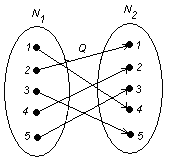
4. ПРЯМОЕ ПРОИЗВЕДЕНИЕ А х В
Прямым произведением множеств А и В называется множество М всех пар (![]() ), таких, что
), таких, что ![]()
Если А=В, то такое произведение называется ![]()
Аналогично можно вывести операцию прямого произведения большего числа множеств.
![]()
![]()
Если в частности ![]() одинаковы
одинаковы ![]() то получаем
то получаем ![]()
(Например, множество точек на плоскости являются прямым произведением двух множеств).
Если множества конечные, мощность произведений ![]() равна мощности произведений
равна мощности произведений ![]()
5. ОСНОВНЫЕ ТОЖДЕСТВА АЛГЕБРЫ МНОЖЕСТВ
Независимость расположения:
![]() (1)
(1)
![]() (2)
(2)
Ассоциативность:
![]() (3)
(3)
![]() (4)
(4)
Дистрибутивность:
![]()
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
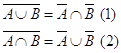
6. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ИХ ПРИМЕНЕНИЕ В ТЕОРИИ МНОЖЕСТВ
Основная задача комбинаторики – пересчет и перечисление элементов в конечных множествах.
1. Если нас интересует, сколько элементов принадлежащих данному конечному множеству обладают некоторым свойством, то это задача пересчета.
2. Если необходимо выделить все элементы множества, обладающие заданными свойствами, то это задача перечисления.
Рассмотрим следующие элементы комбинаторики, позволяющие решать вышеупомянутые задачи. К таким объектам относятся:
- перестановки (с повторением и без них);
- размещения (с повторением и без них);
- сочетания (с повторением и без них);
Перестановками называют комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается ![]() (без повторений).
(без повторений).
Перестановки с повторениями вычисляются по формуле:
![]() , где
, где ![]() - число повторений элементов каждого вида.
- число повторений элементов каждого вида.
Сочетанием называются такие комбинации элементов, которые отличаются между собой в каждой группе только самими элементами (но не порядком их расположения в группе).
![]() (без повторения)
(без повторения)
![]() (с повторением)
(с повторением)
Размещением называются такие комбинации элементов, которые отличаются между собой или самими элементами или порядком их расположения в группе.
![]() (без повторения)
(без повторения)
![]() (с повторением)
(с повторением)
Похожие работы
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
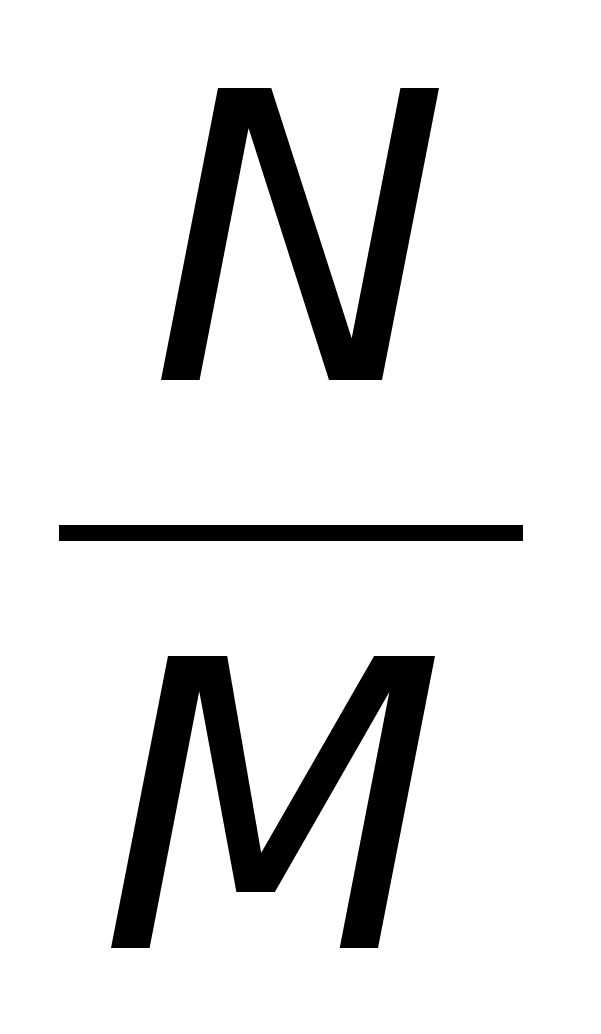
0 комментариев