Навигация
10. БИНАРНЫЕ ОТНОШЕНИЯ
Квадратом множества А называется декартово произведение множества само на себя ![]()
Бинарным отношением Т в множестве А будем называть подмножество его квадрата
![]()
1. Отношение ![]() выполняется для пар (6,8) (6,6)
выполняется для пар (6,8) (6,6)
2. Отношение имеет общий делитель не равный 1. Выполняется для пар (6,4) (4,2) (8,8) но не выполняется для пар (5,4) (3,8)
3. Любые элементы декартова произведения ![]() находятся в бинарном отношении, если
находятся в бинарном отношении, если ![]() , говорят, что
, говорят, что ![]() связаны отношением Т.
связаны отношением Т.
4. Областью значений (изменением бинарного отношения) называется множество ![]() , подчиненное условию
, подчиненное условию
![]()
Как известно из курса математики пару (x,y), где ![]() изображают на координатной плоскости точкой, тогда множество
изображают на координатной плоскости точкой, тогда множество ![]() отобразится координатной плоскостью, а его подмножество, т.е. бинарное отношение отобразится соответствующими графиками этих отношений.
отобразится координатной плоскостью, а его подмножество, т.е. бинарное отношение отобразится соответствующими графиками этих отношений.
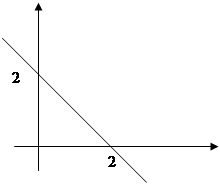
![]()
(1)
![]()
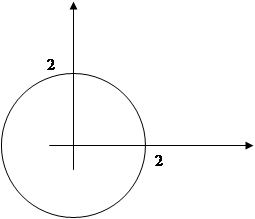
(2)
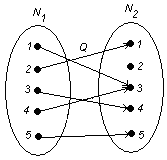
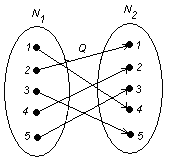
Бинарные отношения на плоскости можно отобразить с помощью графов. Элементы множества ![]() обозначаются вершинами графов. Если пара
обозначаются вершинами графов. Если пара ![]() , то вершины а и в соединяются звеном.
, то вершины а и в соединяются звеном.
Например:
(ав)(вс)(ас)(аа)

11. ОТНОШЕНИЯ ЭКВИВАЛЕНТНОСТИ
Определим некоторые важные свойства бинарных отношений и рассмотрим бинарные отношения, которые обладают тремя из этих свойств и часто встречаются в математике. Такое бинарное отношение называется эквивалентностью.
СВОЙСТВА:
1. 1.1 Пусть ![]() - бинарное отношение,
- бинарное отношение, ![]() - область его задания, тогда
- область его задания, тогда ![]() называется рефлексивным, если
называется рефлексивным, если ![]() , граф таких отношений имеет вид петли при каждой вершине
, граф таких отношений имеет вид петли при каждой вершине
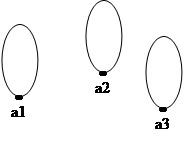
1.2 ![]() называется антирефлексивным, если
называется антирефлексивным, если ![]()
2. 2.1 Отношение может быть симметричным, если
![]() (изображается любым графом)
(изображается любым графом)
2.2 Антисимметричным, если ![]() (изображается ориентированным графом)
(изображается ориентированным графом)
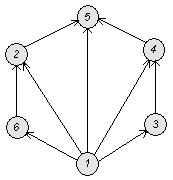
3. 3.1 Транзитивным. Отношение называется транзитивным, если 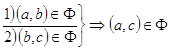 (изображается транзитивным графом – все вершины пересекаются)
(изображается транзитивным графом – все вершины пересекаются)
Если для бинарного отношения ![]() соблюдается три условия: рефлексивность, симметричность и транзитивность, то такое отношение называется эквивалентностью.
соблюдается три условия: рефлексивность, симметричность и транзитивность, то такое отношение называется эквивалентностью.
12. МАТРИЦЫ И ГРАФЫ
Понятие матрицы. Виды матриц. Свойства матриц. Линейные операции над матрицами. Единичные матрицы. Обратные матрицы
Матрицей называется прямоугольная таблица чисел размером ![]() , где m – число строк, а n – число столбцов.
, где m – число строк, а n – число столбцов.
Если m=n – матрица называется квадратной.
Если m-1 – матрица-строка.
Если n=1 – матрица-столбец.
Все числа, входящие в матрицу называются ее элементами. Если все элементы состоят их нулей, то это нулевая матрица, она играет роль нуля в матричном исчислении.
Рассмотрим некоторые линейные операции над матрицами:
1. Сумма
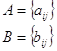
![]()
Исходя из определения можно складывать и вычитать матрицы только одного размера.
2. Произведение матрицы на число называется матрица, где каждый элемент матрицы умножается на это число.
![]()
3. Матрица умножается на матрицу по правилу строка на столбец
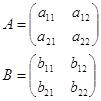
![]()
![]()
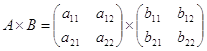
|
такое правило не годится для всех матриц, а именно, количество строк во второй матрице должно равняться количеству столбцов в первой матрице.
Квадратные матрицы перемножаются только одного размера.
4. Единичной матрицей называется квадратная матрица любого размера, где по главной диагонали стоят единицы, а все остальные элементы равны нулю.
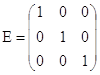 , играет роль единицы в матричном исчислении.
, играет роль единицы в матричном исчислении.
Если такую матрицу умножить на другую матрицу (при возможности умножения) даст исходную матрицу.
![]()
![]() - дельта Кронекера
- дельта Кронекера
5. Обратной матрицей ![]() называется матрица, которая
называется матрица, которая ![]() , заметим, что Е – квадратная, соответственно
, заметим, что Е – квадратная, соответственно ![]() тоже квадратные.
тоже квадратные.
6. ![]() (определитель), если
(определитель), если ![]() , то обратная матрица существует, если
, то обратная матрица существует, если ![]() , то матрица называется вырожденная.
, то матрица называется вырожденная.
Нахождение обратной матрицы
1. Метод присоединенной матрицы
1. 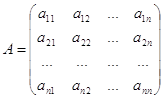
2. 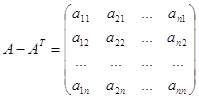
3.
3.1 ![]() (взаимная)
(взаимная)
3.2 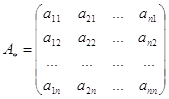
4. ![]()
5. ![]()
2. Метод элементарных преобразований
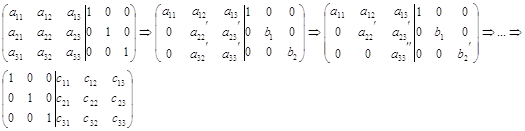
Похожие работы
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
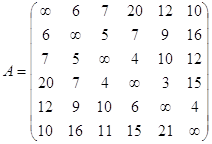
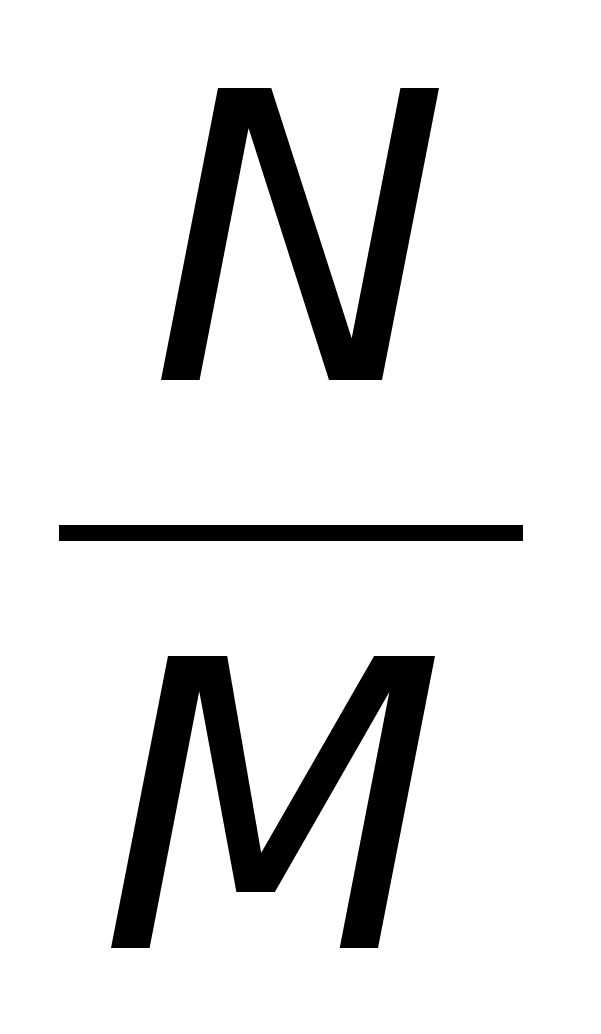
0 комментариев