Навигация
ПРИНЦИПЫ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
12990
знаков
1
таблица
3
изображения
7. ПРИНЦИПЫ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
При вычислении элементов множеств требуется приводить доказательство, по которому вычисляются последующие элементы по предыдущим. Один из алгоритмов этих доказательств – принцип математической индукции.
Этот принцип заключается в следующем:
Пусть при n=1 доказательство очевидно. Принимаем гипотезу, что оно очевидно при n=k, которое не равно 1 (
). Тогда, если доказано, что требуемое равенство очевидно при k+1, то равенство доказано при любом n.
8. ОТОБРАЖЕНИЕ ОТНОШЕНИЯ ФУНКЦИИ
Понятие отображения и функции выражают зависимостью одних переменных величин от других, при этом слово величина может иметь различную смысловую нагрузку. Это может быть элемент любого множества, число, вектор и т.д.
Отображение – множества x во множество y определяется тем, что каждому элементу 
ставится в соответствие 
- графическое изображение отображения, f – обозначение отображения. Закон, который выражается или в виде формулы или в виде алгоритма, т.е. последовательность действий, которые надо предпринять, чтобы получить зависимость элементов множества y от элементов x. Например: всякая нумерация счетного множества является его отображением на множество натуральных чисел N.
Так как отображение может быть истолковано как соответствие, то для того, чтобы показать, что данный элемент x поставлен в соответствие элементу y, пишут 
и говорят, что y есть образ элемента x при данном отображении f.
Пусть x` - подмножество множества x
y` - подмножество множества y
тогда
Совокупность элементов множества x, образом которых является y, называется прообразом и обозначается 
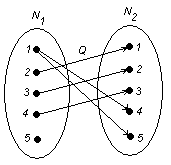
Рассмотрим частные случаи отображения одного множества в другое.
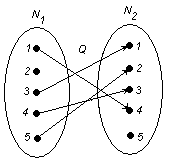
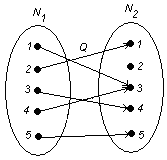
1. Если каждый элемент множества Y имеет прообраз, являяющийся элементом множества X,то в этом случае отображение f называется сюръективным.
2. Отображение f называется инъективным, если для каждого элемента существует не более одного прообраза, т.е. при любых 
, если 
.
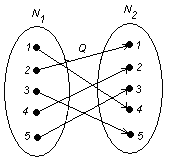
Если отображение f сюръективно и инъективно, то оно называется биеткивным или взаимооднозначным.
Рассмотрим на примере три функции, отображающие множество F действительных чисел само на себя:
1) 
- инъективна, но не сюръективна т.к. 
, однако не каждый y имеет прообраз x т.к. y>0
2) 
- сюръективна, но не инъектина, т.к. y существует при любом x, однако для образа y существует несколько прообразов, т.к. существует несколько корней кубического уравнения 
3) 
- биективна, т.к. x однозначно выражается через x и x однозначно выражается через y.
Два множества называются эквивалентными, если между ними можно установить биективное отображение.
ТОГДА:
Подмножество 
называется функцией 
.
Таким образом функцию можно представить в виде графика, причем множество А – область определения функции, а множество В – область значения функции.
Рассмотрим, например, взаимно однозначное отображение множества R на R1, где R1 есть множество всех положительных чисел 
. Обратным ему будет отображение 
. Для таких отображений справедливо следующее тождество:
9. КОМПОЗИЦИЯ
, то их композицией (произведением) называют 
, причем, если осуществляется композиция, то 
. В математике такое отображение называют сложной функцией, y – промежуточный аргумент.
Для композиции справедливо следующие отображения:
- коммутативное - 
- ассоциативное - 
Похожие работы
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
0 комментариев