МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ

1. МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ

Определение 1.1. Сетью массового обслуживания называется совокупность одновременно и взаимосвязано функционирующих систем массового обслуживания, в которой циркулируют заявки, переходящие из одной системы массового обслуживания в другую.

Определение 1.2. Системы массового обслуживания, из которых состоит сеть, называют узлами (полюсами, обслуживающими центрами).

Определение 1.3. Сеть называется марковской, если она описывается марковским процессом.

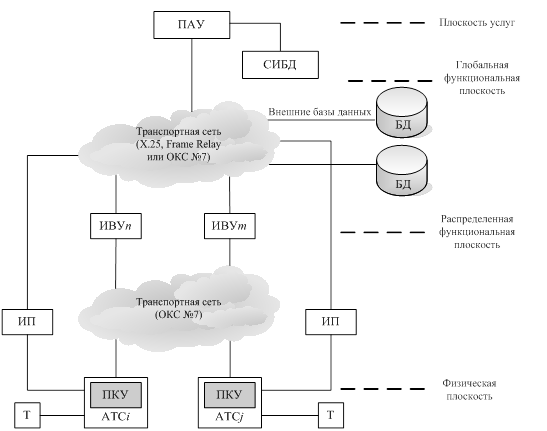
Пусть имеется открытая сеть массового обслуживания, состоящая из трёх узлов, в которую поступает простейший поток заявок с параметром . Причём, в первую систему массового обслуживания, входящая заявка поступает с вероятностью . Времена обслуживания заявок в различных узлах независимы, не зависят от процесса поступления заявок и имеют показательное распределение с параметрами  для -ого узла, где  - число заявок в -ой системе, .

Дисциплины обслуживания заявок в системах сети FCFS. Заявка, завершающая обслуживание в -ом узле мгновенно с вероятностью  переходит в -ый узел или с вероятностью  покидает сеть, причём  . Схематически сеть изображена на рисунке 1.1.

Матрица перехода имеет следующий вид:

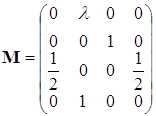
Состояние сети описывается случайным процессом

,

где - число заявок в -ом узле в момент  . Покажем, что - марковский процесс. Состояние  для  определяется:

1)         числом заявок в узлах в момент ;

2)         моментами поступлений заявок в каждый узел после момента ;

3)         моментами ухода заявок из каждого узла после момента .

Лемма 1.1 (об “отсутствии памяти” у показательного распределения).

Если  имеет показательное распределение с параметром , то при любых  и

.

Доказательство. По определению условной вероятности

.

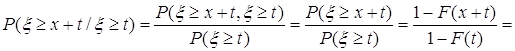
Моменты внешних поступлений в первый узел после момента  не зависят от предыстории сети до момента , так как поток извне на первый узел пуассоновский; моменты поступлений заявок с узлов на данный узел после момента  в силу “отсутствия памяти” у показательного распределения времени обслуживания заявок в узлах (см. лемму 1.1) . Аналогично доказывается, что моменты уходов заявок из узлов после момента  не зависят от предыстории  до момента . Таким образом, закон распределения  для  определяется распределением . Значит,  - марковский процесс. [1]

Таким образом, в соответствии с определением 1.3 и вышесказанном, построена марковская модель открытой сети с тремя узлами.

Похожие работы

Базовый процесс обработки вызовов

Скачать

106915

5

18

... вызова – БПОВ (Basic Call Process, ВСР). BCP взаимодействует с другими блоками посредством точек инициации (Point of Initiation, POI) и завершения (Point of Return, POR). Если в процессе обработки вызова встретится одна из точек инициации, то это приводит к определенной последовательности обращений к блокам SIB. По завершении этой последовательности обращений осуществляется воздействие на процесс ...

Моделирование систем массового обслуживания

Скачать

52202

13

13

... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания   В общем случае СМО классифицируется по следующим признакам: ·  закону распределения входного потока ·  числу обслуживающих приборов ·  закону распределения времени обслуживания в ...