Уравнения глобального равновесия

1.1 Уравнения глобального равновесия

Предположим, что существует стационарное распределение. Составим уравнение равновесия для стационарных вероятностей , которые для сетей называются глобальными уравнениями равновесия (баланса).

Из состояния  сеть может выйти либо за счёт поступления заявки в неё (интенсивность ), либо за счёт обслуживания заявки одним из узлов, например, - ым (интенсивность ). Поэтому интенсивность выхода из состояния  для марковского процесса  равна , где 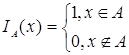 - индикаторная функция множества . Следовательно, поток вероятности из состояния  равен:

. (1.1.1)

Войти же в состояние  можно либо из состояния , если в сеть поступит заявка, направленная в первый узел ( интенсивность ), либо из состояния , если заявка завершит обслуживание во втором узле и уйдёт из сети ( интенсивность ), либо, наконец, из состояний , (,), если заявка завершит обслуживание на первом, (втором, третьем) узле и перейдёт соответственно во второй, ( третий, первый) (интенсивность , (, )). Поэтому поток вероятности в состояние

. (1.1.2)

Приравнивая потоки вероятности из состояния  (формула 1.1.1) и в состояние  (формула 1.1.2), получаем глобальные уравнения равновесия

. (1.1.3)

1.2 Отыскание стационарных вероятностей

Составим уравнение трафика, используя следующую формулу

, (1.2.1)

,

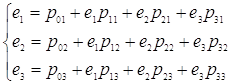где  - вероятности перехода.

Решим полученную систему уравнений

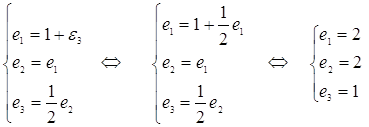
Таким образом, уравнение трафика имеет единственное положительное решение , то есть . Положительное в том смысле, что .

Рассмотрим изолированный -й узел, считая, что на него поступает простейший поток заявок интенсивности  (см. рисунок 1.2.1).

Рисунок 1.2.1

Он представляет из себя систему, отличающуюся от  только тем, что интенсивность обслуживания  зависит от числа заявок в ней , .

Найдем стационарное распределение для такого изолированного процесса. Граф переходов изобразится следующим образом.

0 1 2 …  …

Рисунок 1.2.2

Уравнения равновесия для вертикальных сечений имеют вид ( на рисунке 1.2.2 оно изображено пунктирной линией ).

, , ,

Тогда

.

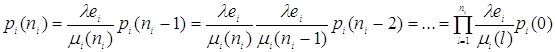Из условия нормировки  находим, что

.

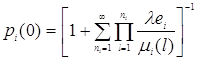Таким образом, , где  равны

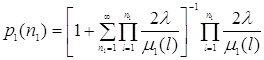, (1.2.2)

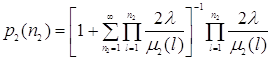, (1.2.3)

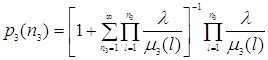.  (1.2.4)

Стационарное распределение  существует и единственно, если выполняется условие эргодичности:

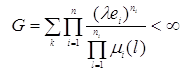 и  (1.2.5)

Теорема 1.2.1.( Разложения Джексона) Пусть уравнение трафика (1.2.1) имеет единственное положительное решение  и выполнено условие эргодичности (1.2.5). Тогда финальные стационарные вероятности состояний сети Джексона имеют вид

, (1.2.6)

где  определяются по формуле

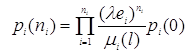, (1.2.7)

в которой  определяется формулой

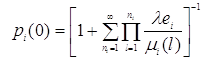. (1.2.8)

Согласно теореме 1.2.1, стационарное распределение представимо в форме произведения множителей характеризующих узлы; каждый множитель есть стационарное распределение узла, то есть

,

где  из формулы (1.2.2),  из формулы (1.2.3),  из формулы (1.2.4).

Таким образом, стационарное распределение имеет следующий вид

 (1.2.9)

=.

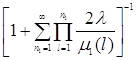
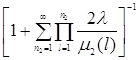
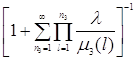
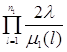
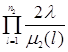
Похожие работы

Базовый процесс обработки вызовов

Скачать

106915

5

18

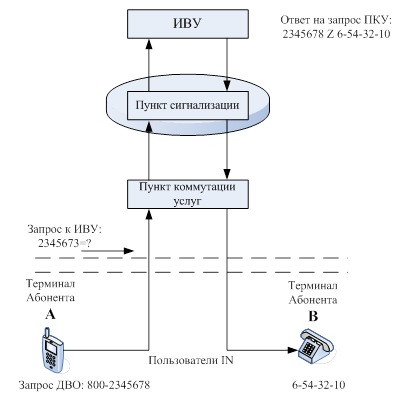
... вызова – БПОВ (Basic Call Process, ВСР). BCP взаимодействует с другими блоками посредством точек инициации (Point of Initiation, POI) и завершения (Point of Return, POR). Если в процессе обработки вызова встретится одна из точек инициации, то это приводит к определенной последовательности обращений к блокам SIB. По завершении этой последовательности обращений осуществляется воздействие на процесс ...

Моделирование систем массового обслуживания

Скачать

52202

13

13

... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания   В общем случае СМО классифицируется по следующим признакам: ·  закону распределения входного потока ·  числу обслуживающих приборов ·  закону распределения времени обслуживания в ...