Навигация
МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ И РАЗНОТИПНЫМИ ЗАЯВКАМИ
3. МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ И РАЗНОТИПНЫМИ ЗАЯВКАМИ
Пусть имеется открытая сеть массового обслуживания, состоящая из трёх узлов, в которую поступают два независимых пуассоновских потока заявок с интенсивностями ![]() и
и ![]() соответственно. Моменты поступления заявки (все равно из какого потока) образуют новый поток, который называется суперпозицией или объединением первоначальных потоков.
соответственно. Моменты поступления заявки (все равно из какого потока) образуют новый поток, который называется суперпозицией или объединением первоначальных потоков.
Обозначим через ![]() ,
, ![]() ,
, ![]() – вероятности поступления
– вероятности поступления ![]() заявок за время
заявок за время ![]() соответственно для потока с интенсивностью
соответственно для потока с интенсивностью ![]() ,
, ![]() , суммарного потока. Так как заявки потоков с интенсивностями
, суммарного потока. Так как заявки потоков с интенсивностями ![]() и
и ![]() поступают независимо друг от друга, то по формуле полной вероятности получим:
поступают независимо друг от друга, то по формуле полной вероятности получим:
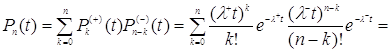
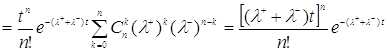 , (3.1)
, (3.1)
то есть суперпозиция пуассоновских потоков с интенсивностью ![]() . [2]
. [2]
Времена обслуживания заявок в различных узлах независимы, не зависят от процесса поступления заявок и имеют показательное распределение с параметрами ![]() для
для ![]() -ого узла,
-ого узла, ![]() - константа (
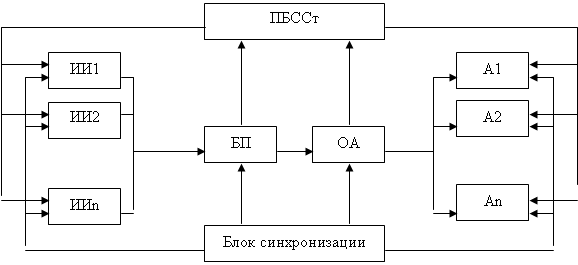
- константа (![]() ). Схематически сеть изображена на рисунке 3.1.
). Схематически сеть изображена на рисунке 3.1.
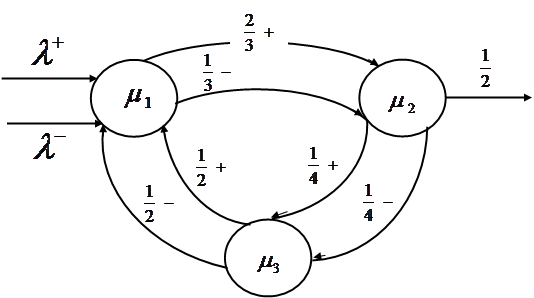
Рисунок 3.1
Заявки поступают двух типов: положительные и отрицательные. Впервые модель введена в работе [8]. На рисунке 3.1 положительные заявки обозначены знаком плюс, а отрицательные знаком минус, ![]() ,
, ![]() – потоки на
– потоки на ![]() -ый узел,
-ый узел, ![]() – поток с
– поток с ![]() -ого узла,
-ого узла, ![]() . На выходе только положительные заявки, дальше положительные заявки разбиваются на положительные и отрицательные.
. На выходе только положительные заявки, дальше положительные заявки разбиваются на положительные и отрицательные.
Дисциплины обслуживания заявок в системах сети определяются следующим образом.
а) Если на приборе нет заявок, то отрицательная заявка, поступающая на прибор, теряется;
б) Если на приборе нет заявок, то поступающая положительная заявка начинает обслуживаться;
в) Если на приборе заявка положительная, то пришедшая отрицательная заявка выбивает заявку с прибора и положительная заявка теряется.
г) Если в очереди ![]() заявок положительных, то приходящая отрицательная заявка, вытесняет последнюю (положительную) заявку и в очереди становится
заявок положительных, то приходящая отрицательная заявка, вытесняет последнюю (положительную) заявку и в очереди становится ![]() заявка (
заявка (![]() -ая положительная и отрицательная заявка теряется).
-ая положительная и отрицательная заявка теряется).
Состояние сети описывается случайным процессом
![]() ,
,
где ![]() – число положительных заявок в момент
– число положительных заявок в момент ![]() , соответственно в первом, втором, третьем узле. В соответствии с разделом 1 и учитывая формулу (3.1)
, соответственно в первом, втором, третьем узле. В соответствии с разделом 1 и учитывая формулу (3.1) ![]() – марковский процесс.
– марковский процесс.
Таким образом, в соответствии с определением 1.3 и вышесказанном, построена марковская модель открытой сети с тремя узлами и разнотипными заявками.
Похожие работы
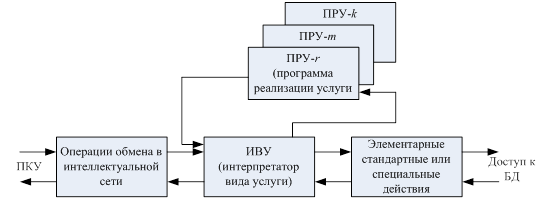
... вызова – БПОВ (Basic Call Process, ВСР). BCP взаимодействует с другими блоками посредством точек инициации (Point of Initiation, POI) и завершения (Point of Return, POR). Если в процессе обработки вызова встретится одна из точек инициации, то это приводит к определенной последовательности обращений к блокам SIB. По завершении этой последовательности обращений осуществляется воздействие на процесс ...
... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания В общем случае СМО классифицируется по следующим признакам: · закону распределения входного потока · числу обслуживающих приборов · закону распределения времени обслуживания в ...
0 комментариев