МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ
Уравнения глобального равновесия
Достаточное условие эргодичности
Дифференциально-разностные уравнения Колмогорова
Поиск решения дифференциально-разностных уравнений Колмогорова
МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ И РАЗНОТИПНЫМИ ЗАЯВКАМИ
Составление уравнений трафика
Нахождение решений уравнений трафика
Уравнения равновесия
Навигация
Дифференциально-разностные уравнения Колмогорова
Марковская и полумарковская модели открытой сети с тремя узлами
26441
знак
3
таблицы
4
изображения
2.1 Дифференциально-разностные уравнения Колмогорова
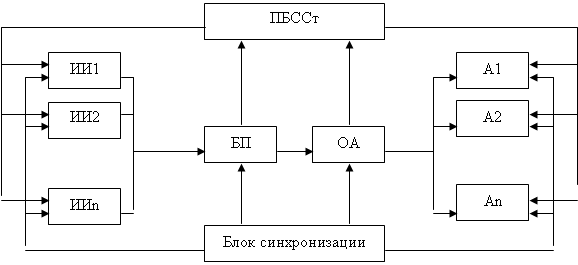
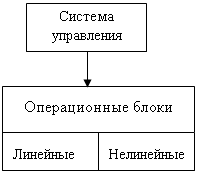
В соответствии методом дифференциальных уравнений и рисунком 2.1, составим следующие уравнения
, (2.1.1)
где 
, 
.
Воспользуемся следующими формулами:
,
[7]
Тогда уравнения (2.1.1) запишутся следующим образом
(2.1.2)
Учитывая то, что некоторые события являются невозможными (они равны нулю), уравнения (2.1.2) примут следующий вид
(2.1.3)
Разложение функции 
в ряд Тейлора, имеет вид
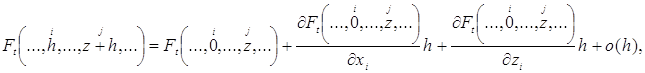
где 
- позиция элемента 
и 
соответственно.
Используя разложение функции в ряд Тейлора, преобразуем уравнения (2.1.3)
.
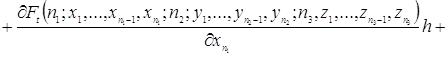
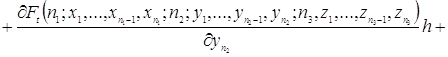
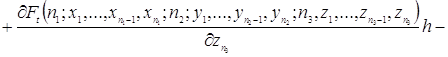
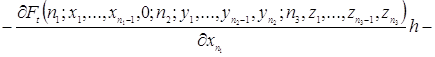
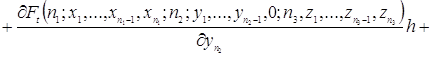
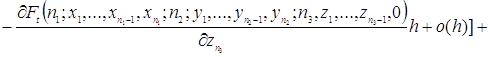
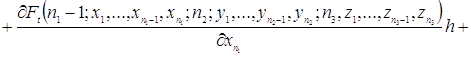
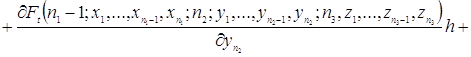
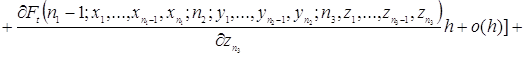
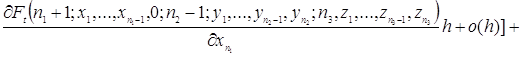
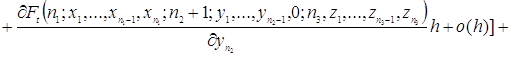
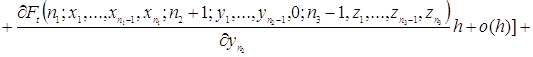
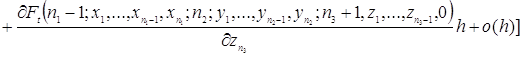Переносим 
в левую часть равенства, затем делим обе части на и устремляем 
, получим
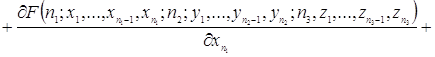
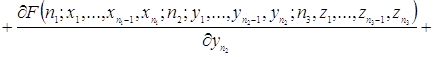
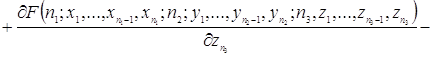
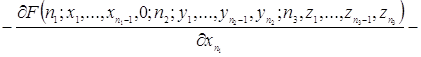
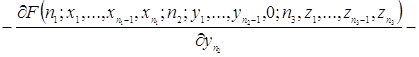(2.1.4)
.
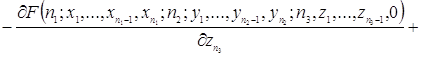
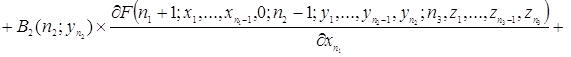
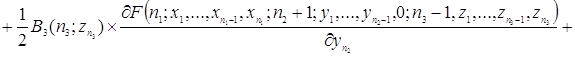
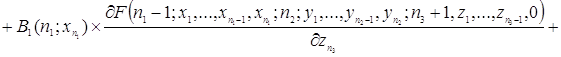
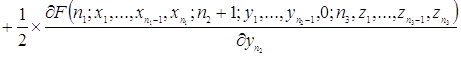Таким образом, уравнения (2.1.4) и есть искомые уравнения Колмогорова.
Похожие работы
... вызова – БПОВ (Basic Call Process, ВСР). BCP взаимодействует с другими блоками посредством точек инициации (Point of Initiation, POI) и завершения (Point of Return, POR). Если в процессе обработки вызова встретится одна из точек инициации, то это приводит к определенной последовательности обращений к блокам SIB. По завершении этой последовательности обращений осуществляется воздействие на процесс ...
... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания В общем случае СМО классифицируется по следующим признакам: · закону распределения входного потока · числу обслуживающих приборов · закону распределения времени обслуживания в ...
0 комментариев