Уравнения равновесия

3.3 Уравнения равновесия

В соответствии, с рисунком 3.1 составим уравнения равновесия

 (3.3.1)

.

3.4 Определение вида стационарного распределения

Стационарное распределение представимо в форме произведения множителей характеризующих узлы; каждый множитель есть стационарное распределение узла, то есть

.

Стационарное распределение -ого узла имеет вид

,

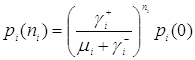где

, .

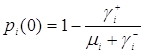Таким образом, стационарное распределение имеет следующий вид

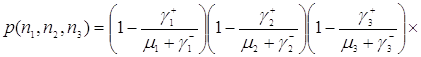
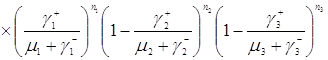. (3.4.1)

Обозначим через

, , .

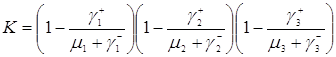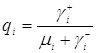Тогда в этих обозначениях формула (3.4.1) запишется в следующем виде

. (3.4.2)

Подставляя формулу (3.4.2) в уравнения равновесия (3.3.1), получим

 (3.4.3)

.

Разделим обе части уравнения (3.4.3) на , получим

 (3.4.4)

.

Через  запишем уравнения трафика (3.1.12) – (3.1.17)

, (3.4.5)

, (3.4.6)

, (3.4.7)

, (3.4.8)

, (3.4.9)

. (3.4.10)

Так как 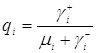, (), то получим следующие соотношения

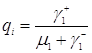, (3.4.11)

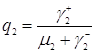, (3.4.12)

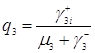. (3.4.13)

Рассмотрим всевозможные случаи числа заявок в марковской модели сети с тремя узлами и разнотипными заявками. То есть следующие случаи

1) , , ;

2) , , ;

3) , , ;

4) , , ;

5) , , ;

6) , , ;

7) , , ;

8) , , ;

Подставляя значения  в уравнение (3.4.4), учитывая уравнения (3.4.5) – (3.4.13), проверим, удовлетворяет стационарное распределение (3.4.1) уравнениям равновесия (3.3.1). Рассмотрим каждый из случаев 1) – 8) отдельно.

Рассмотрим первый случай , ,

.

Согласно формуле (3.4.6) , формуле (3.4.8) , , формуле (3.4.10) , формуле (3.4.9) , получим

,

.

В соответствии с формулой (3.4.5) , формулой (3.4.12) , формулой (3.4.13) . Из формул (3.4.9), (3.4.10) , тогда имеем

,

.

Согласно формуле (3.4.9) , формуле (3.4.10) . Из формул (3.4.7) и (3.4.8) , получим

,

.

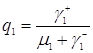А это есть формула (3.4.11), то есть случай 1) выполняется.

Рассмотрим второй случай , ,

,

Согласно формуле (3.4.5) , формуле (3.4.6) , формуле (3.4.8) , , формуле (3.4.10) , формуле (3.4.10) . Из формул (3.4.5) и (3.4.6) . Раскроем скобки и перенесём всё в правую часть, получим

.

В соответствии с формулой (3.4.13) , формулой (3.4.12). Из формул (3.4.9), (3.4.10) , тогда

.

Согласно формуле (3.4.11) , ,формуле (3.4.12) . Из формул (3.4.7) и (3.4.8) , получим

.

, то есть случай 2) выполняется.

Аналогично выполняются 3) – 8).

Таким образом, случаи 1) – 8) превращаются в верное равенство. То есть стационарное распределение (3.4.1) есть решение уравнения равновесия (3.3.1), если выполняется условие эргодичности , .

ЗАКЛЮЧЕНИЕ

В работе проведено исследование открытых марковских и полумарковских сетей массового обслуживания с тремя узлами и циклической маршрутизацией.

Получены следующие основные результаты:

Для марковской модели сети с тремя узлами, записаны уравнения равновесия (формула 1.1.3), получено достаточное условие эргодичности (формула 1.3.1) и найдено стационарное распределение (формула 1.2.9).

Для полумарковской модели сети с тремя узлами, определен вид дифференциально-разностных уравнений Колмогорова (формула 2.1.4), найдено стационарное распределение (формула 2.2.1) и доказана инвариантность (см. 2.3).

Для марковской модели сети с тремя узлами и разнотипными заявками, составлены уравнения равновесия (формула 3.3.1), найдено стационарное распределение (формула 3.4.1) и получено достаточное условие эргодичности (формула 3.2.15).

Результаты работы могут быть применены при проектировании и эксплуатации сетей передачи данных, информационно-вычислительных сетей, сетей ЭВМ и многих других технических объектов.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.         Малинковский Ю.В. Теория массового обслуживания. – Гомель: Бел ГУТ, 1998. – 100с.

2.         Буриков А.Д., Малинковский Ю.В., Маталыцкий М.А. Теория массового обслуживания. – Гродно: ГрГУ, 1984. – 108с.

3.         Ивченко Г.И., Каштанов В.А., Коваленко И.Н. Теория массового обслуживания. – М.: Высшая школа, 1982. – 256с.

4.         Прохоров А.В., Ушаков В.Г., Ушаков Н.Г. Задачи по теории вероят-ностей: Основные понятия. Предельные теоремы. Случайные процессы. – М.: Наука. Главная редакция физ.-мат. литературы, 1986. – 328с.

5.         Кениг Д., Штоян Д. Методы теории массового обслуживания: Пер. с нем.// Под ред. Г.П. Климова. – М.: Радио и связь, 1981. – 128с.

6.         Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. – М.: Наука, 1966. – 431с.

7.         Ширяев А.Н. Вероятность. – М.: Наука. Главная редакция физ.-мат. литературы, 1980 – 575с.

8.         Gelenbe E. Product Form Queueing Networks with Negative and Positive Customers // J. Appl. Probab. – 1991. – V. 28. – P. 656 – 663.

9.         Gelenbe E., Shassberger R. Stability of Product-Form G-networks // Probab. in Eng. and Inform. Sci. – 1992. – No. 6. – P. 271 – 276.

Приложение 1 Список опубликованных работ

1.         Гарбуза И.В. Марковская и полумарковская модели открытой сети с тремя узлами// Материалы V международной межвузовской научно-технической конференции студентов, магистрантов и аспирантов «Исследования и разработка в области машиностроения, энергетики и управления 2005» Гомель, 2005 г.

2.         Гарбуза И.В. Стационарное распределение и его инвариантность для модели открытой сети с тремя узлами// Творчество молодых’2005 Сборник научных работ студентов и аспирантов Гомельского Государственного университета им. Ф. Скорины. Гомель, 2005 г.

Похожие работы

Базовый процесс обработки вызовов

Скачать

106915

5

18

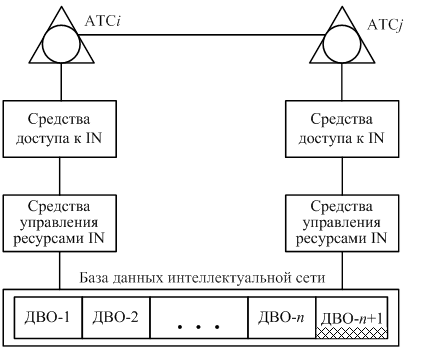
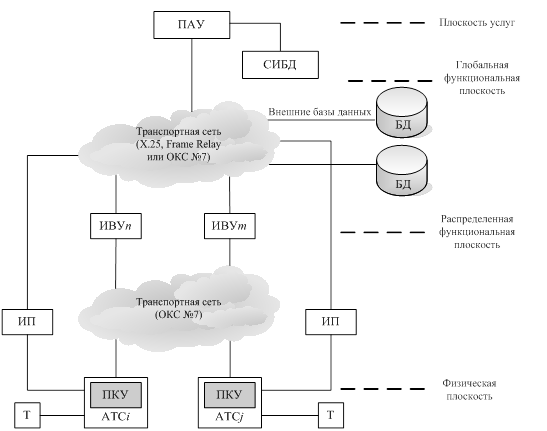
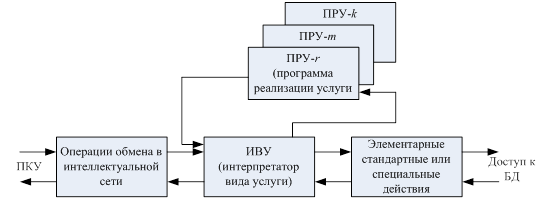
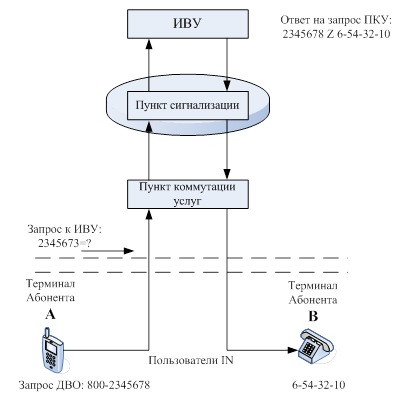
... вызова – БПОВ (Basic Call Process, ВСР). BCP взаимодействует с другими блоками посредством точек инициации (Point of Initiation, POI) и завершения (Point of Return, POR). Если в процессе обработки вызова встретится одна из точек инициации, то это приводит к определенной последовательности обращений к блокам SIB. По завершении этой последовательности обращений осуществляется воздействие на процесс ...

Моделирование систем массового обслуживания

Скачать

52202

13

13

... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания   В общем случае СМО классифицируется по следующим признакам: ·  закону распределения входного потока ·  числу обслуживающих приборов ·  закону распределения времени обслуживания в ...