МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ
Уравнения глобального равновесия
Достаточное условие эргодичности
Дифференциально-разностные уравнения Колмогорова
Поиск решения дифференциально-разностных уравнений Колмогорова
МАРКОВСКАЯ МОДЕЛЬ СЕТИ С ТРЕМЯ УЗЛАМИ И РАЗНОТИПНЫМИ ЗАЯВКАМИ
Составление уравнений трафика
Нахождение решений уравнений трафика
Уравнения равновесия
Навигация
Поиск решения дифференциально-разностных уравнений Колмогорова
Марковская и полумарковская модели открытой сети с тремя узлами
26441
знак
3
таблицы
4
изображения
2.2 Поиск решения дифференциально-разностных уравнений Колмогорова
Решением уравнений Колмогорова (2.1.4) является:
(2.2.1)
.
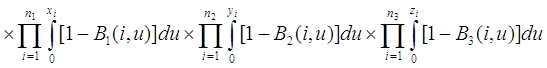Проверим найденное решение (2.2.1) непосредственной подстановкой в уравнения (2.1.4), получим
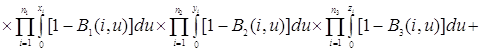
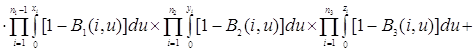
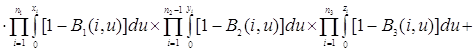
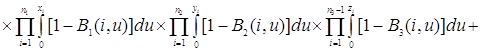
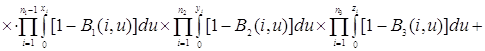
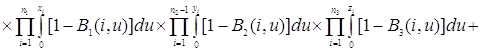
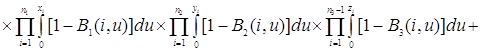
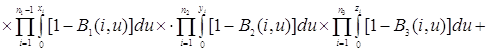
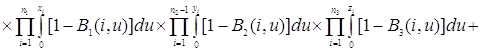
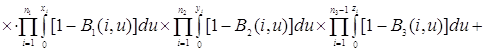
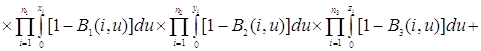
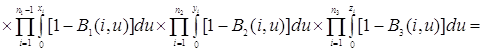
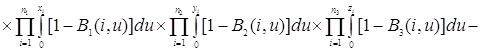
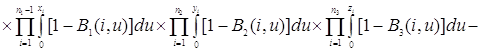
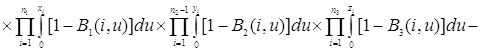
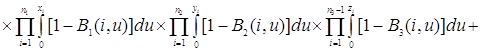
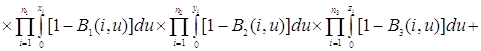
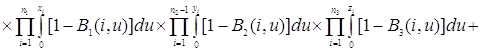
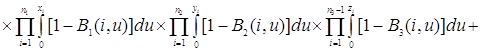
Таким образом, 0=0, то есть решение (2.2.1) удовлетворяет уравнениям (2.1.4).
2.3 Доказательство инвариантности стационарного распределения
Согласно 1.2, для марковской модели сети с тремя узлами получен вид стационарного распределения, который определяется по формуле (1.2.9). При этом времена обслуживания заявок имеют показательное распределение с параметрами 
для 
-ого узла, где 
– число заявок в -ой системе, 
. В соответствии с разделом 2, для полумарковской модели сети с тремя узлами, предполагаем, что длительность обслуживания отдельного требования распределена по произвольному закону. Пусть 
– функция распределения времени обслуживания -ым прибором одной заявки. Предполагается, что выполняется условие, определяемое формулой (2.1).
Согласно результату Севастьянова [6] и формуле (2.2.1), стационарное распределение сохраняет форму произведения (инвариантно) и при допущенных допущениях.
Таким образом, доказана инвариантность стационарного распределения открытой сети массового обслуживания с тремя узлами.
Похожие работы
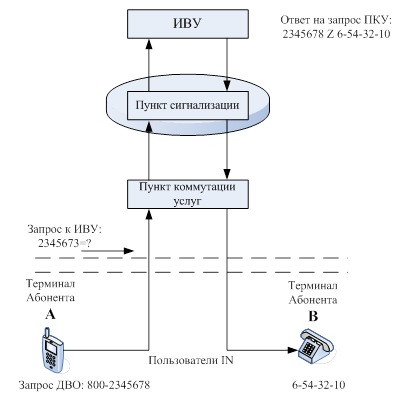
... вызова – БПОВ (Basic Call Process, ВСР). BCP взаимодействует с другими блоками посредством точек инициации (Point of Initiation, POI) и завершения (Point of Return, POR). Если в процессе обработки вызова встретится одна из точек инициации, то это приводит к определенной последовательности обращений к блокам SIB. По завершении этой последовательности обращений осуществляется воздействие на процесс ...
... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания В общем случае СМО классифицируется по следующим признакам: · закону распределения входного потока · числу обслуживающих приборов · закону распределения времени обслуживания в ...
0 комментариев