Нахождение решений уравнений трафика

3.2 Нахождение решений уравнений трафика

Положительность решения уравнений трафика для достаточно общей модели доказана в работе [9].

Для нахождения решений уравнений трафика составим уравнение относительно . Для этого преобразуем формулу (3.1.12), перенесём всё в левую часть и приведём к общему знаменателю

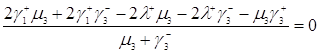. (3.2.1)

Так как , то формула (3.2.1) примет следующий вид

. (3.2.2)

Подставляя формулу (3.1.14) и (3.1.15) в (3.1.16) имеем

.

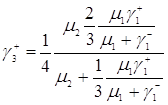Приводим к общему знаменателю

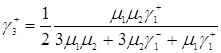. (3.2.3)

Подставим формулу, полученную из формулы (3.1.13) вычетом формулы (3.1.12), получим , в формулу (3.2.3), получим

,

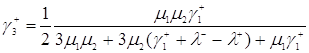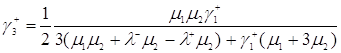. (3.2.4)

Обозначим и , тогда

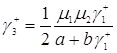. (3.2.5)

В соответствии с формулами (3.1.16) и (3.1.17)

. (3.2.6)

Учитывая формулу (3.2.6) и (3.2.5), получим

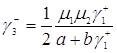. (3.2.7)

Подставим формулы (3.2.5) и (3.2.6) в формулу (3.2.2), имеем

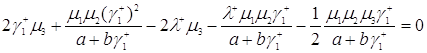. (3.2.8)

Так как , то формула (3.2.8) примет следующий вид

. (3.2.9)

Раскрывая скобки и приводя подобные члены, запишем формулу (3.2.9) в виде

 (3.2.10)

Таким образом, полученное уравнение (3.2.10) квадратное, то есть

, (3.2.11)

где коэффициенты , учитывая обозначения  и формулу (3.2.10), определяются следующим образом

, (3.2.12)

, (3.2.13)

. (3.2.14)

Для уравнения (3.2.11) найдём дискриминант, учитывая формулы (3.2.12), (3.2.13), (3.2.14), имеем

.

Для получения решения уравнения (3.2.11) должно выполнятся следующее условие , а это возможно тогда, когда

.

Согласно формуле , получим

,

то есть

. (3.2.15)

В соответствии с рисунком 3.1, формула (3.2.15) есть условие эргодичности. Если это условие не выполняется, то нет стационарного распределения.

Учитывая формулы (3.2.12), (3.2.14), (3.2.15) получим, что , . Согласно обратной теореме Виета, если  - корни уравнения (3.2.11), то выполняются следующие соотношения

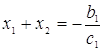
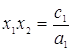
Так как 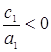, то один из корней положительный и один отрицательный.

Таким образом, уравнение (3.2.11) имеет одно положительное решение. То есть система уравнений трафика (3.1.12) – (3.1.17) имеет положительное решение.

Похожие работы

Базовый процесс обработки вызовов

Скачать

106915

5

18

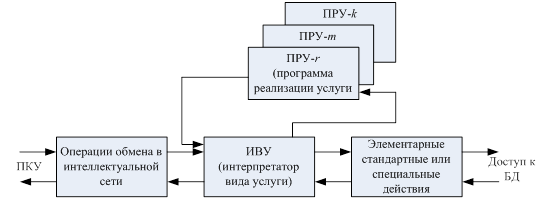
... вызова – БПОВ (Basic Call Process, ВСР). BCP взаимодействует с другими блоками посредством точек инициации (Point of Initiation, POI) и завершения (Point of Return, POR). Если в процессе обработки вызова встретится одна из точек инициации, то это приводит к определенной последовательности обращений к блокам SIB. По завершении этой последовательности обращений осуществляется воздействие на процесс ...

Моделирование систем массового обслуживания

Скачать

52202

13

13

... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания   В общем случае СМО классифицируется по следующим признакам: ·  закону распределения входного потока ·  числу обслуживающих приборов ·  закону распределения времени обслуживания в ...