Общий вид линейной однофакторной модели и её оценки
Оценка параметров модели методом 1МНК
Спецификация модели
Оценка тесноты связи между показателем Y и факторами Х1 и Х2, а также межу факторами. (Диаграмма рассеяния)
Коэффициенты частичной корреляции
Выводы о том, являются ли факторы ведущими и возможной мультиколлнеарности
Оценка параметров модели 1МНК в матричной форме
Коэффициенты множественной детерминации и корреляции для оцененной модели
Разложение коэффициента множественной детерминации на коэффициенты отдельной детерминации
Вычисление стандартных ошибок параметров и выводы о смещенности оценок параметров модели
Проверка значимости оценок параметров модели по критерию Стьюдента
Построение интервалов доверия для параметров модели
Доверительный интервал для прогноза рентабельности
Идентификация переменных
Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера
Навигация
Коэффициенты множественной детерминации и корреляции для оцененной модели
Построение и анализ однофакторной эконометрической модели
38850
знаков
41
таблица
9
изображений
3. Коэффициенты множественной детерминации и корреляции для оцененной модели
3.1 Расчет коэффициентов множественной детерминации и корреляции
Для оценки степени соответствия полученной модели наблюдаемым данным, то есть предварительной оценки адекватности модели, вычисляем коэффициенты множественной детерминации и множественной корреляции.
Коэффициент множественной корреляции является степень соответствия оцененной модели фактическим данным и рассчитывается как коэффициент корреляции между y и 
.
Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации. Коэффициент множественной детерминации характеризует часть дисперсии показателя у, что объясняется регрессией, т.е. вариацией факторов, которые входят в модель:
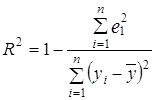
Коэффициент множественной корреляции удобно рассчитывать как корень из коэффициента множественной детерминации, т.е.
Алгоритм вычисления коэффициентов множественной детерминации и корреляции:
1. Скопируем с итогового листа инструмента анализа Регрессия – Регрессия значения столбцов Предсказанное У и Остатки в таблицу 4.
2. Вычислим среднее значение у расчетного
3. В третий столбец введем формулу общих отклонений у-уср. и просчитаем ее для всех наблюдений.
4. Вычислим суммы квадратов общих отклонений и отклонений, которые не объясняются регрессией (остатков).
5. Вычислим коэффициент множественной детерминации 
.
6. Рассчитаем коэффициент множественной корреляции R.
7. Для проверки полученных коэффициентов скопируем с итогового листа Регрессия значения ячеек R-квадрат и Множественный R. Значения совпали.
Таблица 4 – Расчет коэффициентов 
и 
| Факт. | Предсказанное Y | Остатки | Y | Y-Y | |||
| 2,48 | 2,22446 | 0,0955378 | 2,224462 | -0,0167 | |||
| 2,62 | 2,05707 | 0,1329312 | 2,057069 | -0,1467 | |||
| 2,88 | 2,79719 | 0,0328127 | 2,797187 | 0,4933 | По формуле | Регрессия | |
| 2,68 | 2,68606 | 0,0639415 | 2,686058 | 0,4133 | R-квадрат | ||
| 2,52 | 2,5839 | 0,0060977 | 2,583902 | 0,2533 | 0,78 | 0,78 | |
| 2,74 | 2,08937 | 0,1806303 | 2,08937 | -0,0667 | Коеф. мн. корреляций | ||
| 2,56 | 2,30497 | -0,254971 | 2,304971 | -0,2867 | 0,88 | 0,88 | |
| 2,68 | 2,16684 | -0,2168438 | 2,166844 | -0,3867 | |||
| 2,55 | 2,12014 | -0,0401364 | 2,120136 | -0,2567 | |||
| 2,3367 | 2,3367 | ||||||
| 0,17827 | 0,8022 |
Похожие работы
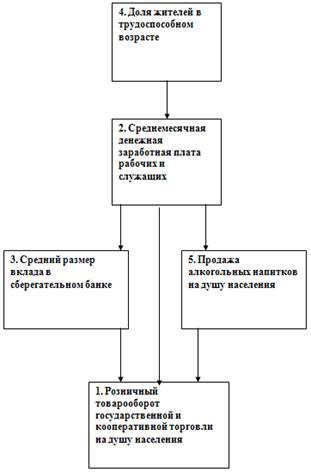
... 53951 20 55,04222 1,857778 21 54,61188 2,388125 22 54,44189 -1,74189 23 54,99919 -1,79919 24 53,51879 0,981207 25 54,09761 -2,99761 Вывод: в результате анализа однофакторной эконометрической модели, характеризующей взаимосвязь между долей жителей в трудоспособном возрасте и среднемесячной денежной заработной платой рабочих и служащих, можно отметить, что модель имеет высокую ...
... , что и в литературе встречается указание на то, что одним из свойств производственной функции является прохождение ее графика через начало координат, (9) свидетельствующее о невозможности выпуска продукции без использования производственных ресурсов. Исходя из сказанного, надо признать, что модели производственной функции линейного типа имеют ограниченную область применения. Поэтому в дальнейшем ...
... метод – 10-4-10-6 Микроскопия – 10-4-10-7 Метод фильтрации – 10-5-10-7 Центрифугирование – 10-6-10-8 Ультрацентрифугирование – 10-7-10-9 Ультрамикроскопия – 10-7-10-9 Нефелометрия – 10-7-10-9 Электронная микроскопия – 10-7-10-9 Метод диффузии – 10-7-10-10 Дисперсионный анализ широко используют в различных областях науки и промышленного производства для оценки дисперсности систем ( ...
... регрессией SSR = ∑(ỹ-y)2 = 3990,5; Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25; Общий разброс данных SSY = ∑(yi-y)2 = 5397,85; Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192; Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками. Вывод: Качество модели хорошее ...
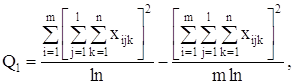
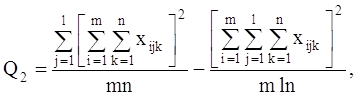
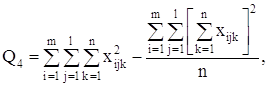
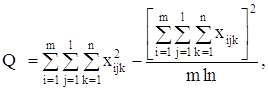
0 комментариев