Общий вид линейной однофакторной модели и её оценки
Оценка параметров модели методом 1МНК
Спецификация модели
Оценка тесноты связи между показателем Y и факторами Х1 и Х2, а также межу факторами. (Диаграмма рассеяния)
Коэффициенты частичной корреляции
Выводы о том, являются ли факторы ведущими и возможной мультиколлнеарности
Оценка параметров модели 1МНК в матричной форме
Коэффициенты множественной детерминации и корреляции для оцененной модели
Разложение коэффициента множественной детерминации на коэффициенты отдельной детерминации
Вычисление стандартных ошибок параметров и выводы о смещенности оценок параметров модели
Проверка значимости оценок параметров модели по критерию Стьюдента
Построение интервалов доверия для параметров модели
Доверительный интервал для прогноза рентабельности
Идентификация переменных
Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера
Навигация
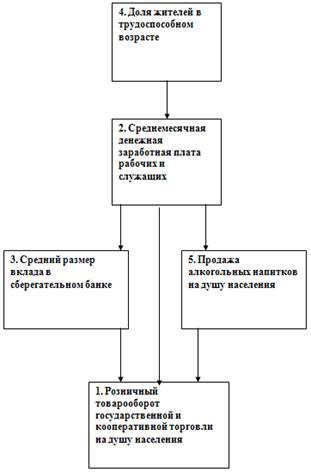
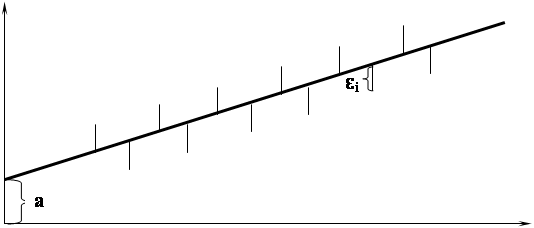
Оценка тесноты связи между показателем Y и факторами Х1 и Х2, а также межу факторами. (Диаграмма рассеяния)
Построение и анализ однофакторной эконометрической модели
38850
знаков
41
таблица
9
изображений
1.2 Оценка тесноты связи между показателем Y и факторами Х1 и Х2, а также межу факторами. (Диаграмма рассеяния)
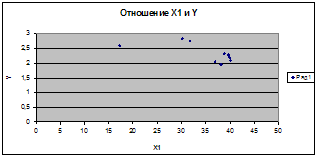
Связь обратная
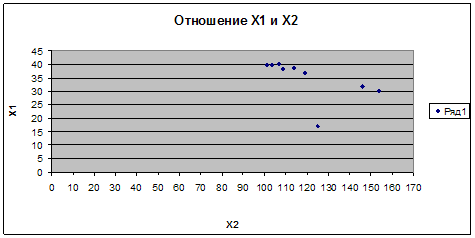
Связь обратная
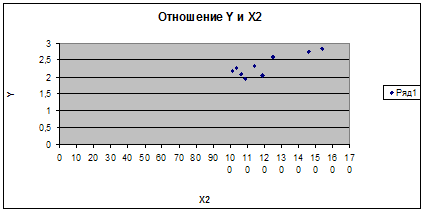
Связь тесная прямая
| Прозноз | ||
| 1) Отношение Х1 и У | ||
| r=-0,5 | ||
| 2) Отношение Х1 и Х2 | ||
| r=-0,4 | ||
| 3) Отношение У и Х2 | ||
| r=0,5 | ||
1.2.1 Парные коэффициенты корреляции, корреляционная матрица
Для оценки тесноты связи между показателем Y и факторами Х1 и Х2, а также между факторами вычисляем парные коэффициенты корреляции, а потом составляем корреляционную матрицу, учитывая ее особенности:
– корреляционная матрица является симметричной;
– на главной диагонали размещены единицы.
Парные коэффициенты корреляции вычисляем по формулам:
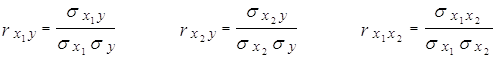
– среднее квадратическое отклонение показателя Y;
– среднее квадратическое отклонение фактора X1;
– среднее квадратическое отклонение фактора X2;
– дисперсия показателя Y;
– дисперсия показателя X1;
– дисперсия показателя X2;
– коэффициент ковариации признаков Y и Х1;
– коэффициент ковариации признаков Y и Х2;
– коэффициент ковариации признаков X1 и Х2;
Таблица 2 – Расчет парных коэффициентов корреляции
| По формуле | Мастер функций | ||
| Дисперсия У | Ср. кв. отклон У | Дисперсия У | Ср. кв. отклон У |
| 0,089133333 | 0,298552061 | 0,089133333 | 0,298552061 |
| Дисперсия Х1 | Ср. кв. отклон Х1 | Дисперсия Х1 | Ср. кв. отклон Х1 |
| 50,16666667 | 7,08284312 | 50,16666667 | 7,08284312 |
| Дисперсия Х2 | Ср. кв. отклон Х2 | Дисперсия Х2 | Ср. кв. отклон Х2 |
| 312,6550617 | 17,68205479 | 312,6550617 | 17,68205479 |
| Ковариация УХ1 | Ковариация УХ1 | ||
| -1,386333333 | -1,386333333 | ||
| Ковариация УХ2 | Ковариация УХ2 | ||
| 4,524851852 | 4,524851852 | ||
| Ковариация Х1Х2 | Ковариация Х1Х2 | ||
| -70,76962963 | -70,76962963 |
Коэффициенты парной корреляции
| rух1 | -0,655601546 | rух1 | -0,655601546 | |
| rух2 | 0,857139597 | rух2 | 0,857139597 | |
| rух1х2 | -0,565075617 | rух1х2 | -0,565075617 |
| Корреляционная матрица |
| |
| 1 | -0,655601546 | 0,857139597 |
| -0,655601546 | 1 | -0,565075617 |
| 0,857139597 | -0,565075617 | 1 |
Похожие работы
... 53951 20 55,04222 1,857778 21 54,61188 2,388125 22 54,44189 -1,74189 23 54,99919 -1,79919 24 53,51879 0,981207 25 54,09761 -2,99761 Вывод: в результате анализа однофакторной эконометрической модели, характеризующей взаимосвязь между долей жителей в трудоспособном возрасте и среднемесячной денежной заработной платой рабочих и служащих, можно отметить, что модель имеет высокую ...
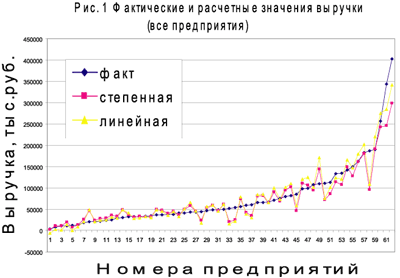
... , что и в литературе встречается указание на то, что одним из свойств производственной функции является прохождение ее графика через начало координат, (9) свидетельствующее о невозможности выпуска продукции без использования производственных ресурсов. Исходя из сказанного, надо признать, что модели производственной функции линейного типа имеют ограниченную область применения. Поэтому в дальнейшем ...
... метод – 10-4-10-6 Микроскопия – 10-4-10-7 Метод фильтрации – 10-5-10-7 Центрифугирование – 10-6-10-8 Ультрацентрифугирование – 10-7-10-9 Ультрамикроскопия – 10-7-10-9 Нефелометрия – 10-7-10-9 Электронная микроскопия – 10-7-10-9 Метод диффузии – 10-7-10-10 Дисперсионный анализ широко используют в различных областях науки и промышленного производства для оценки дисперсности систем ( ...
... регрессией SSR = ∑(ỹ-y)2 = 3990,5; Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25; Общий разброс данных SSY = ∑(yi-y)2 = 5397,85; Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192; Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками. Вывод: Качество модели хорошее ...
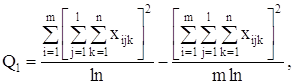
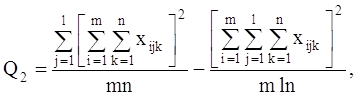
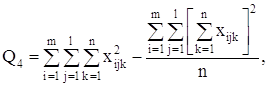
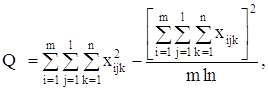
0 комментариев