Навигация
Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера
2. Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера.
Шаг 1. Стандартизация переменных.
Элементы стандартизованных векторов рассчитываются по формулам:
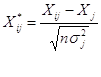 , i=1; n, j=1; m.
, i=1; n, j=1; m.
где n – число наблюдений;
m – число факторов;
σj2 – дисперсия j-го фактора.
Поскольку дисперсия рассчитывается по формуле:
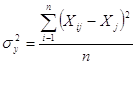 ,
,
то формуле для стандартизации переменных примут вид:
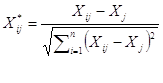 , i=1; n, j=1; m.
, i=1; n, j=1; m.
Шаг 2. Нахождение корреляционной матрицы R (матрицы моментов стандартизованной системы нормальных уравнений).
Корелляционная матрица R определяется по формуле:
R=Х*Т·Х*,
где Х* – матрица стандартизованных переменных.
Для нахождения элементов корелляционной матрицы R последовательно используем встроенные функции Транспонирование матриц – ТРАНСП и Произведение матриц – МУМНОЖ.
Проверку вычислений следует выполнять, и используя последовательно встроенную функцию КОРРЕЛ, учитывая при этом свойства корреляционной матрицы: корреляционная матрица является симметричной, на главной диагонали расположены единицы.
Таблица 2 – Нахождение корреляционной матрицы
| Транспонированная матрица стандартизированных переменных | |||||||||
| -0,01550062 | -0,6665 | -0,1085 | -0,2325092 | -0,171 | 0,14 | 0,32551 | -0,0775 | 0,4495 | 0,3565 |
| -0,87603791 | -0,1057 | -0,09506 | 0,0427594 | 0,2195 | 0,269 | 0,14171 | 0,16291 | 0,2053 | 0,0357 |
| -0,06017464 | 0,89975 | 0,025789 | -0,0028655 | -0,06 | -0,261 | -0,2751 | -0,0458 | -0,189 | -0,0315 |
| Корреляционная матрица | ||||||||
| 1 | 0,222996 | -0,8092664 | Проверка | 1 | 0,223 | -0,809 | ||
| R | 0,223 | 1 | -0,2146624 | R | 0,223 | 1 | -0,215 | |
| -0,8093 | -0,21466 | 1 | -0,8093 | -0,2147 | 1 | |||
Коэффициент корреляции между факторами Х1 и Х2=0,223
Коэффициент корреляции между факторами Х1 и Х3=-0,8093
Коэффициент корреляции между факторами Х2 и Х3=-0,21466.![]()
Вывод: на основании значения коэффициента корреляции rX2X3=-0,21466. можно сделать предварительный вывод о наличии возможной мультиколлинеарности между факторами Х2 и Х3.
Шаг 3. Критерий – Х2.
Расчетное значение критерия Х2 определяется по формуле:
![]() ,
,
где ![]() -определитель корреляционной матрицы R-детерминант корреляции.
-определитель корреляционной матрицы R-детерминант корреляции.
По заданной доверительной вероятности Р и числу степеней свободы
![]() находится табличное значение критерия Х2табл, которое сравнивается с расчетным.
находится табличное значение критерия Х2табл, которое сравнивается с расчетным.
– если Х2расч< Х2табл, то нет оснований отклонить гипотезу об отсутствии мультиколлинеарности в массиве факторов, то есть с принятой надежностью можно утверждать, что в массиве факторов мультиколлинеарность отсутствует;
– если Х2расч> Х2табл, то гипотеза об отсутствии мультиколлинеарности в массиве факторов отклоняется, то есть с принятой надежностью можно утверждать, что в массиве факторов мультиколлинеарность существует.
Примечание: Если гипотеза об отсутствии мультиколлинеарности в массиве факторов принимается, то исследования мультиколлинеарности останавливаются.
Выберем уровень значимости ά=0,05, следовательно доверительная вероятность Р=0,95. Число степеней свободы k=3. Табличное значение критерия Х2табл=Х2(0,95; 3)=7,8.
Исследование наличия мультиколлинеарности в массиве факторов по критерию Х2 в оболочке электронных таблиц Excel.
1. Находим определитель матрицы, используя встроенную функцию МОПРЕД.
2. Находим натуральный логарифм определителя, используя встроенную математическую функцию LN.
3. Находим расчетное значение критерия.
4. Вводим расчетное значение.
5. Делаем вывод о наличии мультиколлинеарности в массиве факторов, используя встроенную логическую функцию ЕСЛИ.
Таблица 3=Критерий Х2.
| Таблица 3 | |
| Определитель корреляционной матрицы | 0,326758051 |
| Натуральный логарифм определителя | -1,118535287 |
| Расчетное значение критерия | 8,016169558 |
| Табличное значение критерия | 7,8 |
| Вывод о наличии в массиве факторов мультиколлиниарности | В массиве факторов существует мультиколлинеарность |
Выводы:
– на основании значения детерминанта корреляции ![]() =0,33 (→0) можно сделать предварительный вывод о наличии мультиколлинеарности в массиве факторов;
=0,33 (→0) можно сделать предварительный вывод о наличии мультиколлинеарности в массиве факторов;
– на основании критерия – Х2 с надежностью Р=0.95 можно утверждать, что в массиве факторов есть мультиколлинеарность.
Шаг 4. F-критерий Фишера.
Расчетные значения F-критерия для каждого фактора определяются по формуле:
![]() , j=1,2…m
, j=1,2…m
где![]() - диагональные элементы матрицы С=R-1;
- диагональные элементы матрицы С=R-1;
По заданной доверительной вероятности Р и числом степеней свободы:
– k1=m-1 – степень свободы знаменателя;
– k2=n-m – степень свободы числителя(k1< k2).
Находится табличное значение F-критерия, которое сравнивается з расчетным:
– если Fjрасч< Fjтабл, то нет оснований отклонить гипотезу об отсутствии мультиколлинеарности между J-тым фактором и остальным массивом, то есть с принятой надежностью можно утверждать, что между J-тым фактором и другими мультиколлинеарность отсутствует;
– если Fjрасч> Fjтабл, то гипотеза об отсутствии мультиколлинеарности между J-тым фактором и остальным массивом отклоняется, то есть с принятой надежностью можно утверждать, что между J-тым фактором и другими мультиколлинеарность существует.
Выбираем уровень значимости ά=0,05, следовательно, доверительная вероятность Р=0,95. Число степеней свободы k1=2, k2=7. Табличное значение критерия F0,95(2; 7)=4,74.
Исследования наличия мультиколлинеарности каждого фактора со всеми другими факторами массива по F-критерию Фишера в оболочке электронных таблиц Excel.
1. Находим расчетные значения критерия F1, F2, F3 соответственно.
2. Вводим табличное значение критерия.
3. Делаем вывод об отсутствии мультиколлинеарности фактора Х1 и факторами Х2 и Х3, используя встроенную логическую функцию ЕСЛИ.
Поскольку функция будет копироваться в остальные ячейки столбца, то при введении адрес ячеек, которые сравниваются, нужно использовать абсолютную и относительную ссылку.
4. Копируем полученную формулу в две нижние ячейки и делаем выводы о наличии мультиколлинеарности фактора Х2 с факторами Х1 и Х3 и Х3 с факторами Х1 и Х2.
Таблица 4-F-критерий Фишера
| Матрица, | 2,91934678 | -0,1508 | 2,3302 |
| обратная корреляционной С | -0,15080461 | 1,056096 | 0,1047 |
| матрице | 2,330157238 | 0,104663 | 2,9082 |
| Значение F1 и вывод | 6,71771373 | Между факторм и другими мультиколлиниарность существует | |
| Значение F2 и вывод | 0,196335919 | Между фактором и другими мультиколлинеарность отсутствует | |
| Значение F3 и вывод | 6,678648215 | Между факторм и другими мультиколлиниарность существует | |
| Табличное значение | 4,74 | ||
| F – критерия |
Выводы:
– между фактором Х1 и факторами Х2 и Х3 существует мультиколлинеарность;
– между фактором Х2 и факторами Х1 и Х3 не существует мультиколлинеарности;
– между фактором Х3 и факторами Х2 и Х1 существует мультиколлинеарность;
Шаг 6. Расчет коэффициентов частичной корреляции.
Коэффициенты частичной корреляции рассчитываются по формулам:
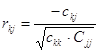 , k=1; m, j=1; m
, k=1; m, j=1; m
где Cjj, Ckk– диагональные элементы матрицы С=R-1
Ckj – элемент матрицы С=R-1, который находится в k-той строке и в j-том столбце.
Поскольку для массива факторов, которые исследуются m=3, то необходимо рассчитывать 3 коэффициента частичной корреляции r12(3), r13(2), r23(1).
Шаг 7. t – критерий Стьюдента.
Расчетные значения t – критерия для каждой пары факторов определяются по формулам:
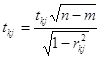 , k=1; m, j=1; m,
, k=1; m, j=1; m,
где rkj – соответствующие коэффициенты частичной корреляции.
По заданной доверительной вероятности З и числом степеней свободы k=n-m находится табличное значение, которое сравнивается с расчетным:
– если tjjрасч<tjjтабл, то нет оснований отклонить гипотезу об отсутствии мультиколлиниарности между k-тым и j-тым факторами, то есть с принятой надежностью можно утверждать, что между k-тым и j-тым факторами мультиколлинеарность отсутствует.
– если tjjрасч>tjjтабл, то гипотеза об отсутствии мультиколлинеарности между k-тым и j-тым факторами отклоняется, то есть с принятой надежностью можно утверждать, что между k-тым и j-тым факторами мультиколлинеарность существует.
Выберем уровень значимости ά=0,05, таким образом, доверительная вероятность Р= 0,95. Число степеней свободы k=7. Табличное значение критерия t0,95(7)=1,89.
Исследование наличия мультиколлинеарности для каждой пары факторов по критерию Стьюдента в оболочке электронных таблиц Excel.
1. Расчетные значения находим по формуле.
2. Вводим табличное значение критерия.
3. Модуль расчетного значения критерия r12(3 находим, используя встроенную математическую функцию ABS, при этом делаем относительную ссылку на столбец.
4. Делаем вывод о наличии мультиколлиниарности между факторами Х1 и Х2, используя встроенную логическую функцию ЕСЛИ. При этом делаем относительную и абсолютную ссылку.
5. Полученную формулу копируем и делаем выводы о наличии мультиколлиниарности между факторами Х1 и Х3, Х2 и Х3.
Таблица 5 – t – критерий Стьюдента
| Коэффициэнты частичной корреляции | |||||||
| r12 (3) | 0,085885547 | ||||||
| r13 (2) | -0,79970784 | ||||||
| r23(1) | -0,10466296 | ||||||
| Значение t-критерия | Модули | Выводы о наличии мультиколлиниарности | |||||
| t12 (3) | 0,228074533 | 0,228075 | Между факторами отсутствует мультиколлинеарность | ||||
| t13 (2) | -3,52409329 | 3,524093 | Между факторома существует мультиколлинеарность | ||||
| t23(1) | -0,27844144 | 0,278441 | Между факторами отсутствует мультиколлинеарность | ||||
| tтабл | 1,89 | ||||||
Выводы: с надежностью Р=0,95 можно утверждать, что:
– между факторами Х1 и Х2 мультиколлинеарность отсутствует;
– между факторами Х1 и Х3 мультиколлинеарность существует;
– между факторами Х2 и Х3 мультиколлинеарность отсутствует;
Общий вывод: Таким образом между факторами 1 и 3 модели, т.е. между относительным уровнем затрат оборота и трудоемкостью существует мультиколлинеарность. Построить модель методом 1МНК нельзя, так как между факторами существует мультиколлинеарность.
Похожие работы
... 53951 20 55,04222 1,857778 21 54,61188 2,388125 22 54,44189 -1,74189 23 54,99919 -1,79919 24 53,51879 0,981207 25 54,09761 -2,99761 Вывод: в результате анализа однофакторной эконометрической модели, характеризующей взаимосвязь между долей жителей в трудоспособном возрасте и среднемесячной денежной заработной платой рабочих и служащих, можно отметить, что модель имеет высокую ...
... , что и в литературе встречается указание на то, что одним из свойств производственной функции является прохождение ее графика через начало координат, (9) свидетельствующее о невозможности выпуска продукции без использования производственных ресурсов. Исходя из сказанного, надо признать, что модели производственной функции линейного типа имеют ограниченную область применения. Поэтому в дальнейшем ...
... метод – 10-4-10-6 Микроскопия – 10-4-10-7 Метод фильтрации – 10-5-10-7 Центрифугирование – 10-6-10-8 Ультрацентрифугирование – 10-7-10-9 Ультрамикроскопия – 10-7-10-9 Нефелометрия – 10-7-10-9 Электронная микроскопия – 10-7-10-9 Метод диффузии – 10-7-10-10 Дисперсионный анализ широко используют в различных областях науки и промышленного производства для оценки дисперсности систем ( ...
... регрессией SSR = ∑(ỹ-y)2 = 3990,5; Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25; Общий разброс данных SSY = ∑(yi-y)2 = 5397,85; Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192; Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками. Вывод: Качество модели хорошее ...




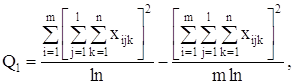
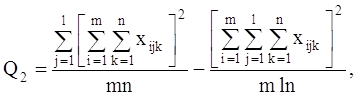
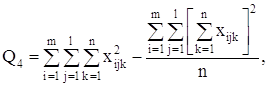
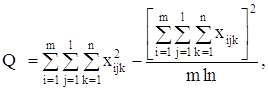

0 комментариев