Метод Ньютона

2.2.1 Метод Ньютона

Якщо виходити з того, що необхідним етапом знаходження рішення задачі:

(2.20)

де f: R^m  R, є етап знаходження стаціонарних точок, тобто точок, задовольняючих рівнянню:

(2.21)

(позначення F для f  ми зберігатимемо), тож можна спробувати вирішувати рівняння (2.21) відомим методом Ньютона рішення нелінійних рівнянь:

xⁿ⁺¹ = xⁿ  [F (xⁿ)]^1F(xⁿ). (2.22)

Для задачі (2.20) цей метод називається методом Ньютона безумовній оптимізації і задається формулою:

xⁿ⁺¹ = xⁿ  [f (xⁿ)]^1f (xⁿ).  (2.23)

Формулу (2.22) можна вивести, виходячи з таких міркувань. Припустімо, що xⁿ — деяке наближене рішення рівняння (2.21). Тоді якщо замінити функцію F в рівнянні (2.21) її лінійним наближенням:

і взяти як наступне наближення рішення рівняння:

  (2.24)

то ми отримаємо формулу (2.22).

Стосовно задачі (2.20) ці міркування виглядають так. Нехай так само, у нас вже є деяке наближене рішення xn задачі (2.20). Замінимо в ній функцію f її наближенням другого порядку:

і як наступне наближення візьмемо рішення задачі:

(2.25)

Та на початку для подальшого використання виведених формул, необхідно довести деякі твердження - якщо f  (xⁿ) > 0, то рішення задачі (2.25) задається формулою (2.23).

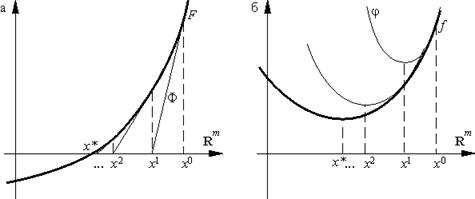
Рис. 2.3 - Геометрична інтерпретація формул (2.22) і (2.23) відповідно

Метод Ньютона відноситься до методів другого порядку, оскільки для обчислення кожної ітерації потрібне знання другої похідної функції f. По тих же міркуваннях градієнтний метод відносять до методів першого порядку. Підкреслимо, що тут йдеться не про порядок збіжності методу, а про порядок використовуються методом похідних функції, що мінімізується.

2.2.2 Теорема про локальну надлінійну збіжність методу Ньютона

Хай f двічі безперервно і може бути диференційована, а x* - не вироджена стаціонарна точка. Тоді знайдеться околиця V_x* точки x* така, що наближення (2.13), початі з довільної початкової точки x⁰V_x* сверх лінійно сходяться до x*.

Доведемо: так як F = f  C¹ і тому

(2.26)

Оскільки F (x*) не вироджений, в силу (2.26) при x достатньо близьких до x* не вироджений і оператор F (x) і більш того,

Тому, зокрема, при x достатньо близьких до x*

||[F (x)]^1||  C. (2.27)

Далі, внаслідок того, що F можна диференціювати, а x*- стаціонарна точка

F(x) = F(x*) + F (x*)(x  x*) + o(x - x*) = F (x*)(x  x*) + o(x - x*),

Але тоді в силу (2.27)

x  x*  [F (x)]^1F(x) = [F (x)]^1F (x)(x  x*)  [F (x)]^1F(x) =

[F (x)]^1[F (x)(x  x*)  F(x)] = o(x  x*).

або

x  [F (x)]^1F(x)  x* = o(x  x*).

Зокрема, при x = xⁿ

 (2.28)

Візьмемо тепер як V_x*, наприклад, околиця {x  R^m: ||(x  x*)||  ||xx*||/2}. В силу (2.28), очевидно, якщо x⁰V_x*, то

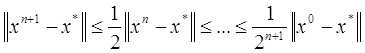
отже, xⁿ  x* при n . Більш того, для довільного q(0, 1) знайдеться >0 таке, що ||(xx*)|| q||xx*|| при ||xx*|| .Але тоді, якщо ||xⁿx*|| то ||xⁿ⁺¹x*|| q||xⁿx*||. З останнього твердження очевидним чином витікає потрібне співвідношення ||xⁿx*|| Cqⁿ .

Таким чином метод Ньютона, з одного боку, може сходитися з більш високим ніж градієнтний метод порядком, а, з другого боку, для його збіжності потрібні достатньо добрі початкові наближення (принаймні так потрібен в доведеній теоремі). Простий геометричний приклад (див. рис. 2.4) підтверджує цю особливість методу (ми наводимо приклад для рівняння (2.21); відповідний приклад для задачі (2.20) виходить „інтеграцією” рис. 2.4).

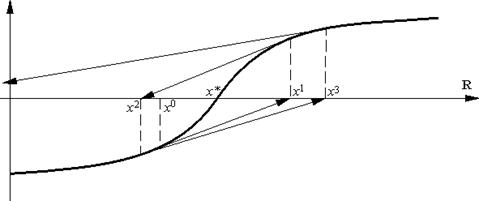
Рис. 2.4 - Геометричне відображення прикладу

Зрозуміло, як метод другого порядку, метод Ньютона вимагає більшого об'єму обчислювальної роботи, оскільки доводиться обчислювати другі похідні функції f.

До цього зводяться основні переваги (високий порядок збіжності) і недоліки (локальний характер збіжності і більший об'єм обчислень) методу Ньютона.

Якщо функція f додатково сильно опукла, то можна затверджувати збіжність саме до рішенню задачі (1), а не тільки до стаціонарної точки функції f, і, крім того, оцінити радіус околиці, з якої наближення Ньютона сходяться.

Похожие работы

Управління банківськими ризиками (на прикладі ВАТ КБ "Іпобанк")

Скачать

188697

38

21

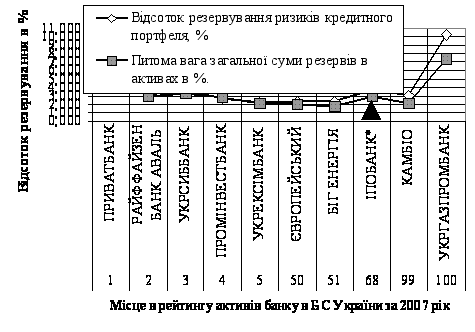
... і чим вартість активів. Чим більше дисбаланс середньозважених термінів погашення, тим більше чуттєвою буде акціонерний капітал банку до змін процентних ставок. РОЗДІЛ ІІ АНАЛІЗ УПРАВЛІННЯ БАНКІВСЬКИМИ РИЗИКАМИ (НА ПРИКЛАДІ ВАТ КБ “ІПОБАНК”) 2.1 Загальна характеристика діяльності та організації ризик-менеджменту в ВАТ КБ “ІПОБАНК” Відкрите акціонерне товариство Комерційний Банк „Іпобанк” працює ...

Споживче кредитування та його розвиток в Україні

Скачать

225295

29

30

... "Догмат Україна" починає з 2002 року. Саме тоді невелика команда активних молодих менеджерів ухвалила стратегічне рішення про входження на український ринок фінансових послуг для населення. Тоді ж були вивчені національні особливості споживчого кредитування, його специфіка і визначені ключові сегменти для подальшого розвитку компанії. Менше ніж через рік, в 2003, була створена торгова марка "Є ...

Маркетингова діяльність комерційного банку

Скачать

169879

18

17

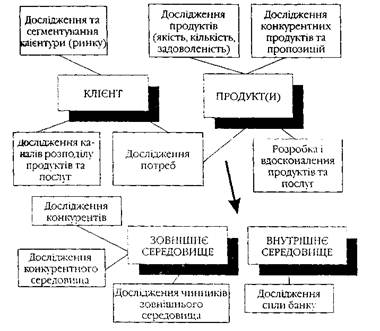
... -споживач (рис.1.1). Рисунок 1.1 - Основні етапи маркетингової роботи Першим, вихідним моментом, обов'язковим для функціонування ринку, є наявність клієнта з його потребами і продукту (послуги), властивості якого дають змогу їх задовольняти. Це необхідна умова комерційного контакту. Дослідження клієнтів містить: - дослідження і сеґментування клієнтури (ринку); - дослідження потреб; - ...

Активи комерційних банків

Скачать

72029

4

3

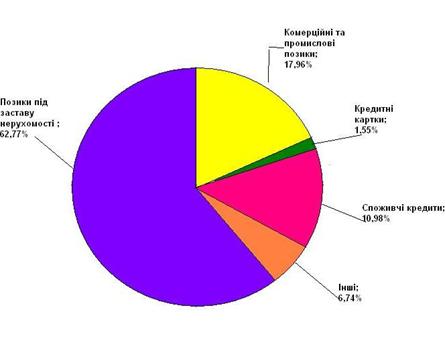
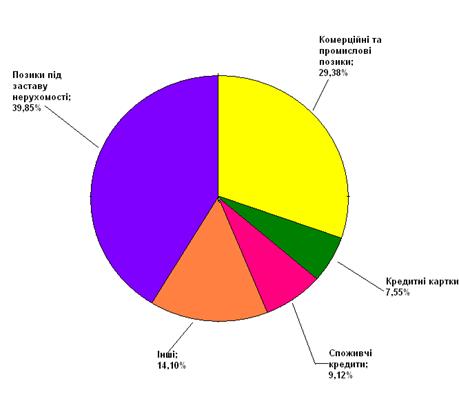
... свідчать діаграми, зображені на рис. 5.1.1, при цьому малими банками там вважаються банки з розміром активів до 1,0 млрд дол, відповідно, великими - з активами 1,0 млрд дол і більше. Рис.3.1 Структура кредитного портфеля комерційних банків СІЛА (2001 рік)   Малі банки Великі банки   У документі можуть бути визначені географічні райони, де ба­жана кредитна експансія банку. Залежно від ...