ОГАНІЗАЦІЙНО-ЕКОНОМІЧНА ХАРАКТЕРИСТИКА
Організаційна структура ДФ АБ "Правексбанк"
Літературний огляд
Постановка задачі
Методи оптимізації
Метод Ньютона
Теорема про квадратичну збіжність методу Ньютона
ОПТИМІЗАЦІЯ БАНКІВСЬКИХ ПОСЛУГ
Оптимізація банківських послуг
Аналіз отриманих результатів і оцінка економічної ефективності запропонованих методів
ОРГАНІЗАЦІЯ БЕЗПЕЧНИХ УМОВ ПРАЦІ ПРИ РОБОТІ З ЕЛЕКТРОННО-ОБЧИСЛЮВАЛЬНИМИ МАШИНАМИ
Вимоги до працівників перед початком роботи
Розробка заходів щодо поліпшення умов праці
Навигация
Теорема про квадратичну збіжність методу Ньютона
Розвиток теорії надання банківських послуг на прикладі ДФ АБ "Правексбанк"
110266
знаков
18
таблиц
12
изображений
2.2.3 Теорема про квадратичну збіжність методу Ньютона
Хай f C2 і, більш того, f задовольняє умові Липшиця з константою L. Хай f сильно випукла с константою . Хай Vx* - околиця рішення задачі (2.10), що складається з точок x Rm таких, що
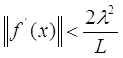
Тоді для x0 Vx* метод Ньютона квадратично сходиться:
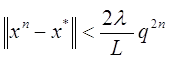
де q = L||f (x0)||/22 < 1.
По теоремі 2.9 і 2.10 в умовах нашої теореми рішення x* задачі (2.10) існує і єдино. Скористаємося аналогом формули Ньютона-Лейбніца для функції f :
Віднімаючи з обох частин цієї рівності 
враховуючи, що f задовольняє умову Липшиця, одержуємо (ср.):
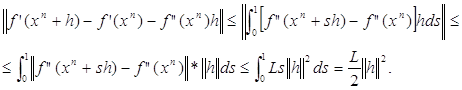
Покладемо в отриманій оцінці h = [f (xn)]1f (xn):
(2.29)
Також необхідно довести, що якщо оборотний лінійний оператор А на Rm задовольняє оцінці А і , то ||A1|| .
Оскільки f сильно опукла, в силу задачі (2.25), f (xn) і тому (див. попер. задачу) ||[f (xn)]1|| 1. Продовжуючи нерівність (2.19), одержуємо:
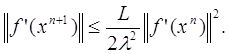(2.30)
З допомогою (2.30) індукцією по n легко доводиться нерівність:
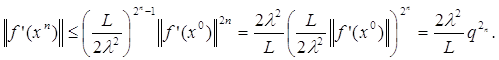(2.31)
Нарешті, в силу сильної випуклості f, оскільки x* — рішення задачі (2.20) і, отже, f (x*) = Q,
0 f(x*) f(xn) (f (xn), x* xn) + ||xn x*|| 2,
або
(f (xn), xn x*) || xn x*|| 2.
Але тоді
||xn x*|| 2 (f (x*), xn x*) ||f (x*)|| · ||xn x*||,
звідки ||f (x*)|| || xn x*||. Тоді з (2.31) слідує потрібна нерівність.
З доведеної теореми витікає, що чим менше константа Липшиця відображення x f (x), тобто чим ближче це відображення до константи, і, отже, чим ближче функція f до квадратичної, тим швидше сходиться метод Ньютона. Зокрема, якщо f квадратична: f(x) = (Ax, x)/2 + (b, x) + c, то метод Ньютона кінцевий, а саме, сходиться за один крок, причому з будь-якої початкової точки.
Якщо понизити вимоги гладкості на функцію f, наприклад, відмовитися від умов Липшиця для f , то швидкість збіжності, взагалі кажучи, падає.
Покажемо, що f(x)= |x|5/2 метод Ньютона сходиться лише лінійно.
Метод Ньютона навіть для сильно випуклих функцій в загальному випадку сходиться лише локально. Опишемо модифікації цього методу, які можуть володіти властивістю глобальної збіжності. Ці методи ще називають методами Ньютона — Рафсона, або демпфованими методами Ньютона. Вони будуються аналогічно з градієнтними методами с перемінним кроком. Загальний вид їх такий:
xn+1 = xn n[f (xn)]1f (xn).
Довжина кроку може вибиратися за допомогою алгоритму дроблення кроку, вимагаючи, наприклад, виконання нерівності:
f(xn+1)=f(xnn[f (xn)]1f (xn))
f(xn) n(f (xn), [f (xn)]1f (xn)),
або, як в методі самого скорішого спуска, вважаючи
n = argmin0{f(xn [f (xn)]1f (xn))}.
Можна показати, що методи Ньютона — Рафсона для сильно випуклих функцій глобально квадратично сходяться (принаймні для описаних вище алгоритмів вибору кроку), причому оддалік точки мінімуму вони сходяться лінійно.
Похожие работы
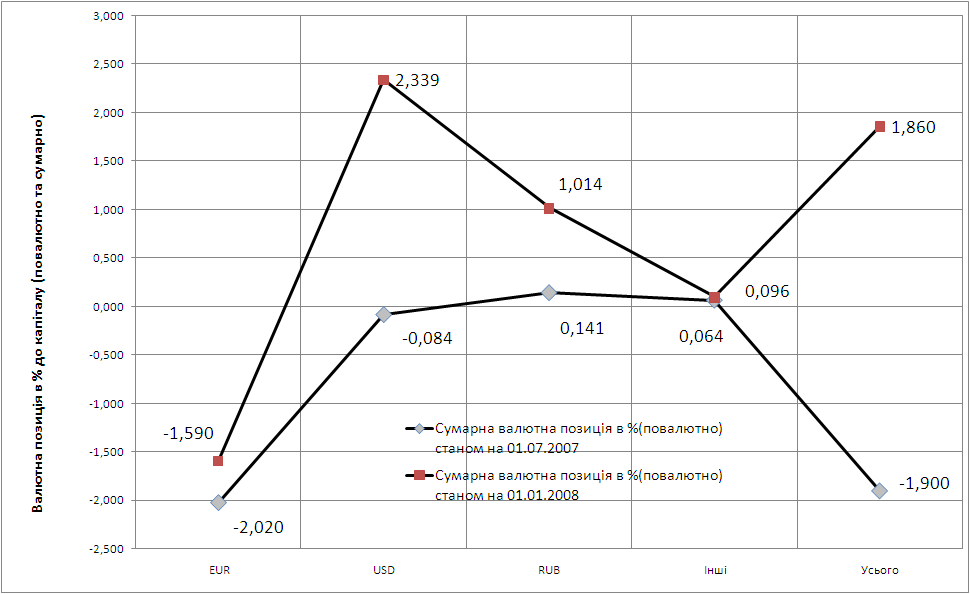
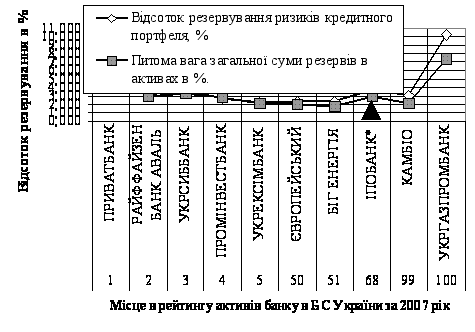
... і чим вартість активів. Чим більше дисбаланс середньозважених термінів погашення, тим більше чуттєвою буде акціонерний капітал банку до змін процентних ставок. РОЗДІЛ ІІ АНАЛІЗ УПРАВЛІННЯ БАНКІВСЬКИМИ РИЗИКАМИ (НА ПРИКЛАДІ ВАТ КБ “ІПОБАНК”) 2.1 Загальна характеристика діяльності та організації ризик-менеджменту в ВАТ КБ “ІПОБАНК” Відкрите акціонерне товариство Комерційний Банк „Іпобанк” працює ...
... "Догмат Україна" починає з 2002 року. Саме тоді невелика команда активних молодих менеджерів ухвалила стратегічне рішення про входження на український ринок фінансових послуг для населення. Тоді ж були вивчені національні особливості споживчого кредитування, його специфіка і визначені ключові сегменти для подальшого розвитку компанії. Менше ніж через рік, в 2003, була створена торгова марка "Є ...
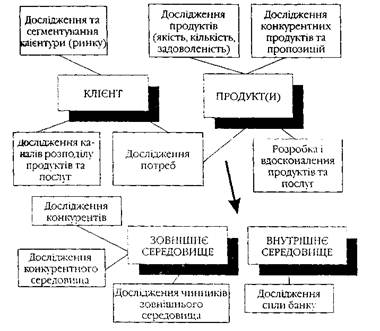
... -споживач (рис.1.1). Рисунок 1.1 - Основні етапи маркетингової роботи Першим, вихідним моментом, обов'язковим для функціонування ринку, є наявність клієнта з його потребами і продукту (послуги), властивості якого дають змогу їх задовольняти. Це необхідна умова комерційного контакту. Дослідження клієнтів містить: - дослідження і сеґментування клієнтури (ринку); - дослідження потреб; - ...
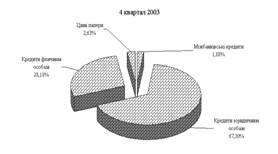
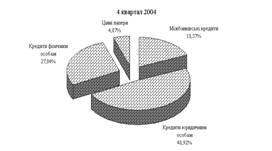
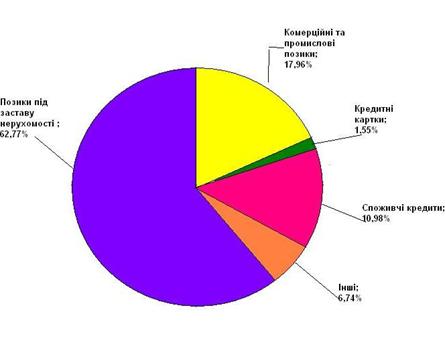
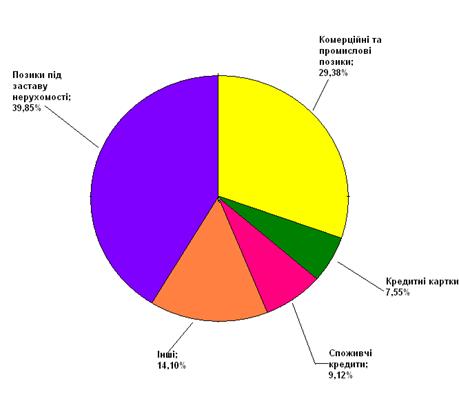
... свідчать діаграми, зображені на рис. 5.1.1, при цьому малими банками там вважаються банки з розміром активів до 1,0 млрд дол, відповідно, великими - з активами 1,0 млрд дол і більше. Рис.3.1 Структура кредитного портфеля комерційних банків СІЛА (2001 рік) Малі банки Великі банки У документі можуть бути визначені географічні райони, де бажана кредитна експансія банку. Залежно від ...
0 комментариев