Навигация
Дії над матрицями
2. Дії над матрицями
Додавання матриць
Додавання матриць вводиться тільки для матриць одного порядку. Сумою двох матриць ![]() і
і ![]() порядку (m x n) називається матриця
порядку (m x n) називається матриця ![]() , яка має такий самий порядок (m x n), причому кожен елемент матриці
, яка має такий самий порядок (m x n), причому кожен елемент матриці ![]() дорівнює сумі відповідних елементів матриць
дорівнює сумі відповідних елементів матриць ![]() і
і ![]() :
:
![]() .
.
Множення числа на матрицю
Добутком числа ![]() на матрицю
на матрицю ![]() порядку (m x n) називається матриця
порядку (m x n) називається матриця ![]() порядку (m x n), кожний елемент якої дорівнює добутку числа
порядку (m x n), кожний елемент якої дорівнює добутку числа ![]() на відповідний елемент матриці
на відповідний елемент матриці ![]() :
:
![]()
 .
.
Для додавання і множення матриць на число справедливі такі операції:
![]() а)
а) ![]()
- комутативний закон додавання матриць;
![]() б)
б) ![]()
![]() - асоціативний закон додавання матриць;
- асоціативний закон додавання матриць;
в) ![]()
![]() - асоціативний закон множення чисел на матрицю;
- асоціативний закон множення чисел на матрицю;
г) ![]()
![]() - дистрибутивний закон множення числа на суму матриць;
- дистрибутивний закон множення числа на суму матриць;
ґ) ![]()
- дистрибутивний закон множення суми чисел на матрицю.
Добуток матриць
Добуток двох матриць вводиться лише для узгоджених матриць. Дві матриці ![]() і
і ![]() називаються узгодженими, якщо кількість стовпців першої матриці
називаються узгодженими, якщо кількість стовпців першої матриці ![]() дорівнює кількості рядків другої матриці
дорівнює кількості рядків другої матриці ![]() .
.
Якщо матриці ![]() порядку (m x n) і
порядку (m x n) і ![]() порядку (n x p) узгоджені, то добутком цих матриць називається матриця
порядку (n x p) узгоджені, то добутком цих матриць називається матриця ![]() порядку (m x p), для якої елемент
порядку (m x p), для якої елемент ![]() дорівнює добутку кожного елемента і-го рядка матриці
дорівнює добутку кожного елемента і-го рядка матриці ![]() на j-й стовпець матриці
на j-й стовпець матриці ![]() .
.
![]() Взагалі операція множення матриць не комутативна:
Взагалі операція множення матриць не комутативна:
![]() .
.
Квадратну матрицю можна помножити саму на себе, тобто піднести до квадрата.
Для дій над матрицями справедливі такі властивості:
![]() а)
а) ![]()
![]() - асоціативний закон множення матриць;
- асоціативний закон множення матриць;
б) ![]()
![]()
![]() - дистрибутивний закон множення матриці на суму матриць;
- дистрибутивний закон множення матриці на суму матриць;
в) ![]()
- комутативний закон множення квадратної матриці ![]() на одиничну матрицю
на одиничну матрицю ![]() такого ж порядку.
такого ж порядку.
Транспонування матриць
Матриця ![]() ’ називається транспонованою відносно матриці
’ називається транспонованою відносно матриці ![]() , якщо кожен стовпець матриці
, якщо кожен стовпець матриці ![]() ’ є відповідним рядком матриці
’ є відповідним рядком матриці ![]() , тобто перший стовпець матриці
, тобто перший стовпець матриці ![]() ’є першим рядком матриці
’є першим рядком матриці ![]() , відповідно другий стовпець матриці
, відповідно другий стовпець матриці ![]() ’ є другим рядком матриці
’ є другим рядком матриці ![]() і т.д.
і т.д.
Для елементів транспонованих матриць виконується умова
![]()
![]() .
.
Якщо квадратна матриця ![]() симетрична, то виконується умова
симетрична, то виконується умова ![]() .
.
Властивості транспонованих матриць:
1. ![]()
2. ![]()
![]()
3. ![]()
4. ![]()
Інвертування матриць
Розглянемо невироджену матрицю n-го порядку:
![]()
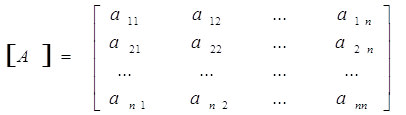 .
.
Квадратна матриця ![]() називається невиродженою, якщо її визначник не дорівнює нулю, тобто
називається невиродженою, якщо її визначник не дорівнює нулю, тобто ![]() , і виродженою, якщо її визначник дорівнює нулю, тобто
, і виродженою, якщо її визначник дорівнює нулю, тобто ![]() .
.
Квадратна матриця ![]() називається оберненою до квадратної матриці
називається оберненою до квадратної матриці ![]() того ж порядку, якщо їх добуток дорівнює одиничній матриці:
того ж порядку, якщо їх добуток дорівнює одиничній матриці:
Визначення рангу матриці
Якщо у будь-якій матриці виділити r довільних столбців та r довільних рядків, то з елементів матриці, які містяться на перетині цих рядків і стовпців, можна скласти визначник r-го порядку. Його називають мінором r-го порядку.
Рангом матриці називають число, яке дорівнює найвищому порядку її мінора, відмінного від нуля (rang [A]).
Диференціальне обчислювання в матричній формі
Розглянемо деякі випадкидиференціального обчислювання в матричній формі, які використовуються в економетриці.
1.Похідна від скалярного добутку векторів (![]() ) по одному з них дорівнює другому:
) по одному з них дорівнює другому:
![]()
![]() .
.
2.Розглянемо добуток ![]() , де А – квадратна симетрична матриця порядку n, x – вектор розмірністю n.
, де А – квадратна симетрична матриця порядку n, x – вектор розмірністю n.
![]()
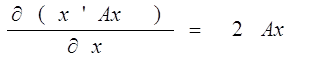
![]() або
або
![]() .
.
![]() .
.![]()
3. Друга частинна похідна по вектору х :
![]()
![]() .
.
2. Для побудови та аналізу економетричних моделей, а також для прогнозування економічних процесів застосовується ряд професійних пакетів прикладних програм. Такими є пакет STATGRAFICS, SPSS. В рамках лабораторної роботи необхідно поверхньо ознайомитися з призначенням цих пакетів, їх функціональними можливостями та особливостями, а також послідовністю операцій, які виконуються з їх застосуванням.
Завдання для самостійної роботи студентів Завдання 1.1 Згадати правила виконання операцій з матрицями (додавання, множення, транспонування, інвертування, диференціювання). Завдання 1.2Виконати дії над матрицями:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (E – одинична матриця).
(E – одинична матриця).
Вихідні дані для розрахунків:
 , abc – три останні цифри шифру студента,
, abc – три останні цифри шифру студента,
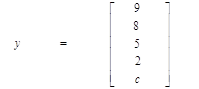 .
.
Лабораторна робота № 2
Тема. Парна лінійна регресія
Мета роботи: навчитися будувати парну лінійну регресійну модель економічних процесів.
Завдання1. На основі спостережених даних показника Y і фактора X знайти оцінки:
1) коефіцієнтів кореляції і детермінації;
2) параметрів лінії регресії ![]() .
.
2. Побудувати ANOVA-таблицю для парної регресії.
3. Використовуючи критерій Фішера, з надійністю P=0.95 оцінити адекватність прийнятої моделі статистичним даним.
4. Розрахувати інші показники якості моделі.
5. Використовуючи t-статистику, з надійністю Р=0.95 оцінити значущість коефіцієнта кореляції.
6. Використовуючи t-статитстику, з надійністю Р=0.95 оцінити значущість параметрів моделі та визначити інтервали довіри для параметрів.
7. Якщо модель адекватна статистичним даним, то знайти:
1) з надійністю Р=0.95 надійні зони базисних даних;
2) точковий прогноз показника;
3) інтервальні прогнози показника та його математичного сподівання.
8. На основі одержаної економетричної моделі зробити висновки.
Хід роботи1. 1) Коєфіцієнт кореляції є мірою щільності зв’язку між змінними.
Коєфіцієнт кореляції між двома рядами спостережуваних змінних X та Y розраховується за формулою:
![]()

Коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції.
3) Вводиться гіпотеза, що між фактором Х та показником Y існує лінійна стохастична залежність
![]() .
.
Оцінки параметрів ![]() та
та ![]() парної регресіїобчислюються методом 1МНК за формулами:
парної регресіїобчислюються методом 1МНК за формулами:
![]()
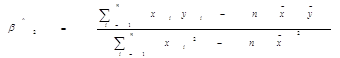 ,
,
(або
![]()
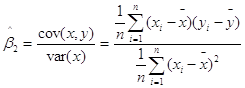 )
)
![]()
![]() ,
,
де n – кількість спостережень.
Для роботи використовується пакет EXCEL. Складається розрахункова таблиця за макетом (табл.2.1) і розраховуються оцінки параметрів:
Таблиця 2.1 Розрахункова таблиця для оцінки параметрів парної лінійної моделі (за формулами (2.1), (2.3))
| № спостереження | X | Y | XY | X2 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | ||||
| 2 | ||||
| … | ||||
| n | ||||
| Сума | x | х | ||
| Середнє значення | х | х | ||
| Прогнозне значення |
Результат розрахунків – вектор параметрів ![]() .
.
2. Для проведення дисперсійного аналізу складається ANOVA-таблиця (табл. 2.2):
Таблиця 2.2ANOVA-таблиця
| Джерело варіації | Кількість ступенів вільності | Сума квадратів | Середні квадрати |
| Зумовлене регресією (модель) | К-1 |
|
|
| Не пояснюване за допомогою регресії (помилка) | n-K |
|
|
| Загальне | n-1 |
| - |
У разі парної регресії К=2 – кількість оцінюваних параметрів.
Для розрахунку ANOVA-таблиці розрахункова табл. 2.1 додається такими графами :
Продовження табл. 2.1
| № спостереження |
| ( |
| ( | ( |
| 1 | 6 | 7 | 8 | 9 | 10 |
| 1 | |||||
| 2 | |||||
| … | |||||
| n | |||||
| Сума | 0 | ||||
| Середнє значення | х | Х | 0 | х | х |
| Прогнозне значення |
Похожие работы
... комбiнацiю просторової i часової вибірок n × m × T. Проблема формування сукупності спостережень та її однорiдностi досить важлива в економетричному моделюванні, бо економетрична модель кiлькiсно описує закономiрнiсть формування економічних процесів та явищ. А ця закономiрнiсть доволі повно може проявитись лише тоді, коли сукупність спостережень достатньо велика. Якщо дослідник задає ...
... собою системи взаємопов'язаних рівнянь і використовуються для кількісних оцінок параметрів економічних процесів та явищ. За внесок у розвиток економетричних моделей і методів 1969 р. Нобелівську премію одержали Р. Фріш і Я. Тінберген. 1980 р. за створення економічних моделей і застосування їх до аналізу економічних коливань і економічної політики Нобелівську премію одержав Л. Юіяйн. За пояснення ...
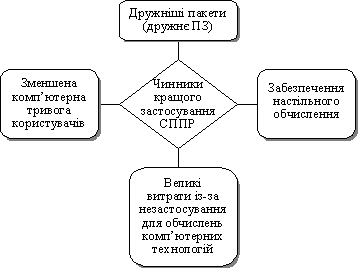
... інші території. На додаток до цього моделі прогнозування в СППР та основані на реальних знаннях системи часто використовуються як настільні, розраховані на одного користувача системи. Системи підтримки прийняття рішень набули широкого застосування в економіках передових країн світу, причому їхня кількість постійно зростає. На рівні стратегічного управління використовується ряд СППР, зокрема для ...
... банківському ринку намагається досягнути банк, а також з загальним рівнем характеристик усередненого банку банківської системи України; В якості банка - лідера для зовнішньоекономічної орієнтації діяльності ВАТ “Міжнародний комерційний банк” виберемо ВАТ “Державний акціонерний експортно-імпортний банк України" (810 рейтингове місце в банківській системі України - дивись Додаток А [98]), в якості ...

0 комментариев