Навигация
Оцінити параметри моделі за методом 1МНК (у матричній формі). Інтерпретувати отримані оцінки
1. Оцінити параметри моделі за методом 1МНК (у матричній формі). Інтерпретувати отримані оцінки.
2. Оцінити стандартизовані регресійні коефіцієнти ("бета-коефіцієнти"). Інтерпретувати оцінені стандартизовані коефіцієнти регресії.
3. Скласти до числового прикладу вектори ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]()
![]()
а також матриці X та D.
4. Розрахувати значення величин ![]() ,
, ![]() ,
, ![]() .
.
5. Оцінити еластичність товарообігу відносно торговельної площі та відносно середньоденної частоти потоку покупців, обчисливши коефіцієнти еластичності.
6. Перевірити значимість окремих коефіцієнтів регресії (провести t-тестування), визначити їх інтервали довіри.
7. Розрахувати та інтерпретувати коефіцієнт детермінацї, частинний коефіцієнт детермінації та зкоректований коефіцієнт детермінації.
8. Перевірити модель на адекватність за допомогою F-критерію Фішера.
9.У разі адекватності моделі обчислити та інтерпретувати для регресії:
- точковий прогноз товарообігу t+1-го філіалу;
- 99%-ний прогнозний інтервал математичного сподівання товарообігу цього філіалу;
-
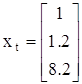 |
99%-ний прогнозний інтервал безпосередньо самого товарообігу yt+1 цього філіалу, якщо задані такі значення регресорів:
Хід роботи
1. Для знаходження вектора оцінок параметрів багатофакторної лінійної моделі застосовується метод 1МНК у матричній формі:
![]()
![]()
Параметри лінійної регресії інтерпретуються так: зміна величини к-го регресора на одиницю свого виміру за інших рівних умов призведе до зміни оціненої величини ![]() на число одиниць свого виміру, яке дорівнює значенню
на число одиниць свого виміру, яке дорівнює значенню ![]() .
.
2. Стандартизовані коефіцієнти регресії обчислюються за формулою:
![]()
![]() , (k=2,…,k),де
, (k=2,…,k),де
![]() 1МНК-оцінка регресійного коефіцієнта
1МНК-оцінка регресійного коефіцієнта ![]() ;
;
![]() - емпіричне стандартне (середньоквадратичне) відхилення k-го регресора xk
- емпіричне стандартне (середньоквадратичне) відхилення k-го регресора xk
![]()
![]()
![]() - емпіричне стандартне (середньоквадратичне) відхилення регресанда y.
- емпіричне стандартне (середньоквадратичне) відхилення регресанда y.
![]()
![]()
Емпіричний стандартизований регресійний коефіцієнт ![]() вказує на те, який великий за інших рівних умов типовий ефект впливу k-го регресора у порівнянні з типовим ефектом зміни регресанда.
вказує на те, який великий за інших рівних умов типовий ефект впливу k-го регресора у порівнянні з типовим ефектом зміни регресанда.
3. Складаються такі вектори і матриці:
 - вектор спостережуваних значень показника Y;
- вектор спостережуваних значень показника Y;
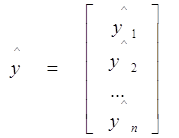 - вектор оцінених значень регресанда;
- вектор оцінених значень регресанда;
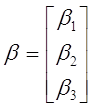 - вектор дійсних, але невідомих параметрів регресії;
- вектор дійсних, але невідомих параметрів регресії;
 - вектор 1МНК-оцінок параметрів моделі;
- вектор 1МНК-оцінок параметрів моделі;
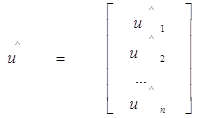 - 1МНК-оцінка вектору помилок;
- 1МНК-оцінка вектору помилок;
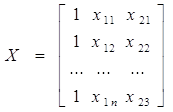 - матриця регресорів;
- матриця регресорів;
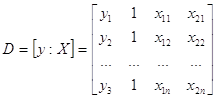 - матриця даних.
- матриця даних.
4. Розраховуються величини: ![]() - суму помилок регресії (має дорівнювати 0),
- суму помилок регресії (має дорівнювати 0), ![]() - суму квадратев помилок,
- суму квадратев помилок, ![]() - дисперсію помилок.
- дисперсію помилок.
![]()
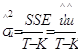
5. Коефіцієнти еластичності розраховуються за формулою:
![]() ,
,
де ![]() - значення регресанда і к-го регресора, що визначають точку регресійної функції, для якої обчислюється коефіцієнт еластичності. Можна використовувати
- значення регресанда і к-го регресора, що визначають точку регресійної функції, для якої обчислюється коефіцієнт еластичності. Можна використовувати ![]() та
та ![]() - середні значення.
- середні значення.
Похожие работы
... комбiнацiю просторової i часової вибірок n × m × T. Проблема формування сукупності спостережень та її однорiдностi досить важлива в економетричному моделюванні, бо економетрична модель кiлькiсно описує закономiрнiсть формування економічних процесів та явищ. А ця закономiрнiсть доволі повно може проявитись лише тоді, коли сукупність спостережень достатньо велика. Якщо дослідник задає ...
... собою системи взаємопов'язаних рівнянь і використовуються для кількісних оцінок параметрів економічних процесів та явищ. За внесок у розвиток економетричних моделей і методів 1969 р. Нобелівську премію одержали Р. Фріш і Я. Тінберген. 1980 р. за створення економічних моделей і застосування їх до аналізу економічних коливань і економічної політики Нобелівську премію одержав Л. Юіяйн. За пояснення ...
... інші території. На додаток до цього моделі прогнозування в СППР та основані на реальних знаннях системи часто використовуються як настільні, розраховані на одного користувача системи. Системи підтримки прийняття рішень набули широкого застосування в економіках передових країн світу, причому їхня кількість постійно зростає. На рівні стратегічного управління використовується ряд СППР, зокрема для ...
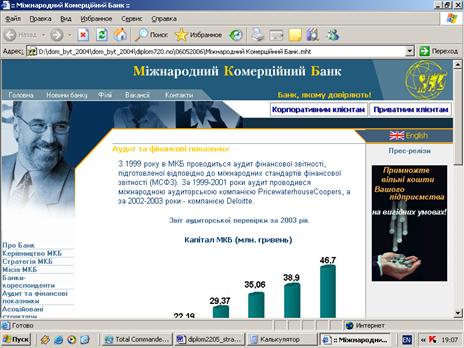
... банківському ринку намагається досягнути банк, а також з загальним рівнем характеристик усередненого банку банківської системи України; В якості банка - лідера для зовнішньоекономічної орієнтації діяльності ВАТ “Міжнародний комерційний банк” виберемо ВАТ “Державний акціонерний експортно-імпортний банк України" (810 рейтингове місце в банківській системі України - дивись Додаток А [98]), в якості ...

0 комментариев