Навигация
Оцінювання середнього та сумарного значення популяції
1.1 Оцінювання середнього та сумарного значення популяції
Введемо поняття кластеру. Кластер – це група одиниць популяції, яка розглядається як вихідна одиниця вибірки. Нехай ![]() . Популяцію можна розбити на
. Популяцію можна розбити на ![]() кластерів, у кожному з яких знаходиться n одиниць. Тоді процедура випадкового відбору систематичної вибірки
кластерів, у кожному з яких знаходиться n одиниць. Тоді процедура випадкового відбору систематичної вибірки ![]() го порядку така ж сама, як і процедура вибору одного із
го порядку така ж сама, як і процедура вибору одного із ![]() кластерів (див. табл. 1.1.1).
кластерів (див. табл. 1.1.1).
Таблиця 1.1.1 Можливі систематичні вибірки ![]() го порядку
го порядку
| Страти | Кластер | Середнє страти | |||||
| 1 | 2 | … | i | … | k | ||
| 1 |
|
| … |
| … |
|
|
| 2 |
|
| … |
| … |
|
|
| … | … | … | … | … | … | … | … |
|
|
|
| … |
| … |
|
|
| Середнє систематичної вибірки |
|
| … |
| … |
| |
Нехай випадкова величина ![]() – середнє значення систематичної вибірки, тобто
– середнє значення систематичної вибірки, тобто ![]() з імовірністю
з імовірністю ![]() дорівнює значенню
дорівнює значенню ![]() ,
, ![]() .
.
Розподіл ![]() має вигляд
має вигляд
![]() ~
~![]() .
.
Теорема 1.1.1. Середнє значення ![]() систематичної вибірки є незміщеною оцінкою для середнього значення популяції
систематичної вибірки є незміщеною оцінкою для середнього значення популяції ![]() .
.
Доведення.
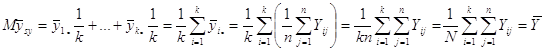 ,
,
де ![]() -ий член
-ий член ![]() -тої систематичної вибірки,
-тої систематичної вибірки, ![]() ,
, ![]() ,
,
зокрема, дисперсія ![]() дорівнює
дорівнює
![]() .
.
Теорема доведена.
Теорема 1.1.2. Дисперсія середнього значення систематичної вибірки визначається формулою
![]() (1.1.1)
(1.1.1)
Де
![]()
є дисперсією одиниць, які належать одній систематичній вибірці (wsy − від англ. within − всередині та systematic − систематичний).
Доведення.
Дисперсія популяції з ![]() одиниць визначається формулою
одиниць визначається формулою
![]() .
.
Розглянемо тотожність
![]() .
.
Піднесемо обидві частини рівності до квадрату
![]() .
.
Підсумуємо праву та ліву частини рівності за ![]() та
та ![]() :
:
![]()
![]()
Покажемо, що ![]() :
:
![]()
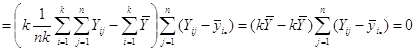
Отже, маємо
![]() ,
,
![]() .
.
Дисперсія ![]() дорівнює
дорівнює
![]()
(обчислена за таблицею розподілу ![]() ). Тоді
). Тоді
![]() .
.
Звідси
![]() ,
,
або, що теж саме,
![]() .
.
Теорема доведена.
Наслідок. Середнє значення для систематичної вибірки більш точне, ніж середнє для простої випадкової вибірки, тобто
![]()
тоді і тільки тоді, коли
![]() . (1.1.2)
. (1.1.2)
Доведення.
Дисперсія середнього значення простої випадкової вибірки дорівнює
![]() .
.
Тоді з (1.1.1) випливає, що ![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]() .
.
Звідси маємо
![]() .
.
Домножимо обидві частини нерівності на ![]() та праворуч винесемо
та праворуч винесемо ![]() :
:
![]() .
.
Враховуючи, що ![]() маємо
маємо
![]() ,
,
або,
![]() .
.
Отже , ![]() .
.
Наслідок доведено.
Таким чином, систематичний відбір точніший, ніж простий випадковий відбір, якщо дисперсія ![]() одиниць систематичних вибірок більша дисперсії
одиниць систематичних вибірок більша дисперсії ![]() всієї популяції. Систематичний відбір точний, коли одиниці всередині однієї й тієї ж вибірки неоднорідні, та неточний, коли вони однорідні. До цього можна прийти інтуїтивно. Якщо всередині систематичної вибірки варіація у порівнянні з варіацією популяції невелика, то послідовно вибрані одиниці вибірки несуть більш або менш однакову інформацію. Інший вираз для дисперсії наведемо у теоремі 1.1.3.
всієї популяції. Систематичний відбір точний, коли одиниці всередині однієї й тієї ж вибірки неоднорідні, та неточний, коли вони однорідні. До цього можна прийти інтуїтивно. Якщо всередині систематичної вибірки варіація у порівнянні з варіацією популяції невелика, то послідовно вибрані одиниці вибірки несуть більш або менш однакову інформацію. Інший вираз для дисперсії наведемо у теоремі 1.1.3.
Теорема 1.1.3.
![]() , (1.1.3)
, (1.1.3)
де ![]() - коефіцієнт кореляції між парами одиниць, що належать до однієї й тієї самої систематичної вибірки. Цей коефіцієнт визначається за формулою
- коефіцієнт кореляції між парами одиниць, що належать до однієї й тієї самої систематичної вибірки. Цей коефіцієнт визначається за формулою
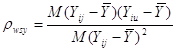 ,
,
де чисельник є середнім по всім ![]() різним парам, а знаменник – середнє по всім
різним парам, а знаменник – середнє по всім ![]() значенням
значенням ![]() . Розпишемо чисельник і знаменник:
. Розпишемо чисельник і знаменник:
![]()
![]()
Підставивши отримані вирази у ![]() отримаємо:
отримаємо:
![]() .
.
Доведення.
Дисперсія середнього значення ![]() систематичної вибірки дорівнює
систематичної вибірки дорівнює
![]() .
.
Звідси маємо
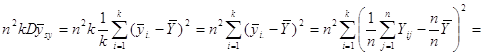
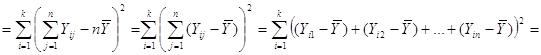
![]()
![]() .
.
Отже,
![]()
![]() .
.
Ділимо обидві частини на ![]() і отримуємо вираз для
і отримуємо вираз для ![]()
![]()
![]() .
.
Останній результат показує, що додатна кореляція між одиницями в одній і тій самій вибірці збільшує дисперсію вибіркового середнього. Навіть мала додатна кореляція може мати великий ефект за рахунок множника ![]() .
.
Теорема доведена.
Дві попередні теореми виражали ![]() через дисперсію популяції
через дисперсію популяції ![]() , тобто співвідносили дисперсію
, тобто співвідносили дисперсію ![]() з дисперсією для простої випадкової вибірки
з дисперсією для простої випадкової вибірки
![]() .
.
Існує аналог теореми 1.1.3, в якому ![]() виражена через дисперсію стратифікованої випадкової вибірки, де страти складалися з перших
виражена через дисперсію стратифікованої випадкової вибірки, де страти складалися з перших ![]() одиниць, других
одиниць, других ![]() одиниць і т.п. При позначеннях індекс
одиниць і т.п. При позначеннях індекс ![]() при
при ![]() відповідає номеру страти. Середнє для страти будемо записувати так
відповідає номеру страти. Середнє для страти будемо записувати так ![]() .
.
Теорема 1.1.4.
![]() , (1.1.4)
, (1.1.4)
![]()
![]() – дисперсія одиниць, що належать до однієї й тієї самої страти. В знаменнику стоїть
– дисперсія одиниць, що належать до однієї й тієї самої страти. В знаменнику стоїть ![]() , тому що кожна з
, тому що кожна з ![]() страт вносить
страт вносить ![]() ступінь вільності. Величина
ступінь вільності. Величина
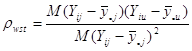 .
.
є коефіцієнтом кореляції між відхиленнями від середнього значення для страти по всім парам одиниць, що належать до однієї й тієї ж систематичної вибірки.
![]() . (1.1.5)
. (1.1.5)
Доведення.
Доведення цієї теореми аналогічно доведенню теореми 1.1.3.
Дисперсія середнього значення ![]() систематичної вибірки дорівнює
систематичної вибірки дорівнює
![]()
Розпишемо середнє значення популяції ![]() через середнє стратифікованої вибірки
через середнє стратифікованої вибірки ![]() :
:
![]() {
{![]() - це
- це ![]() -та одиниця
-та одиниця ![]() -ї страти}
-ї страти}![]()
![]() .
.
Отже маємо
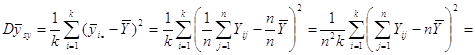
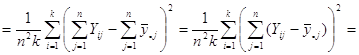
![]()
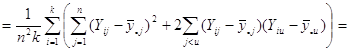
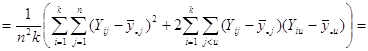
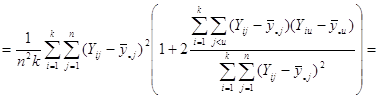
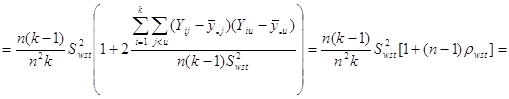
![]() .
.
Отже,
![]() .
.
Теорема доведена.
Наслідок. Якщо ![]() , то систематична вибірка має ту саму точність, що й відповідна стратифікована випадкова вибірка з однією одиницею у кожній страті.
, то систематична вибірка має ту саму точність, що й відповідна стратифікована випадкова вибірка з однією одиницею у кожній страті.
Це твердження випливає з того, що для такої стратифікованої випадкової вибірки ![]() дорівнює:
дорівнює:
![]() .
.
Теорема 1.1.5. Дисперсія величини ![]() , яка використовується для оцінювання сумарного значення популяції
, яка використовується для оцінювання сумарного значення популяції ![]() , дорівнює
, дорівнює
![]() .
.
Приклад. У таблиці 1.1.2 наведені данні для невеликої штучної популяції, яка показує тенденцію до досить стійкого зростання значень ознаки у послідовності одиниць. Маємо ![]() ,
, ![]() ,
, ![]() . Кожний стовпчик відповідає деякій систематичній вибірці, а рядки є стратами. Приклад ілюструє ситуацію, коли кореляція «всередині страт» додатна. Наприклад, у першій вибірці кожне з чотирьох чисел (0, 6, 18, 26) менше середнього значення у страті, до якого воно належить. Це справедливо, з невеликим винятком, для перших п’яти систематичних вибірок. В останніх п’яти вибірках відхилення від середніх значень для страт в основному додатне. Таким чином, члени суми у виразі для
. Кожний стовпчик відповідає деякій систематичній вибірці, а рядки є стратами. Приклад ілюструє ситуацію, коли кореляція «всередині страт» додатна. Наприклад, у першій вибірці кожне з чотирьох чисел (0, 6, 18, 26) менше середнього значення у страті, до якого воно належить. Це справедливо, з невеликим винятком, для перших п’яти систематичних вибірок. В останніх п’яти вибірках відхилення від середніх значень для страт в основному додатне. Таким чином, члени суми у виразі для ![]() переважно додатні. Відповідно до теореми 1.1.4 можна очікувати, що систематичний відбір буде менш точним, ніж стратифікований випадковий відбір з однією одиницею у кожній страті.
переважно додатні. Відповідно до теореми 1.1.4 можна очікувати, що систематичний відбір буде менш точним, ніж стратифікований випадковий відбір з однією одиницею у кожній страті.
Таблиця 1.1.2 Данні по 10 систематичним вибіркам при обсязі вибірок ![]() та обсязі популяції
та обсязі популяції![]()
| Страта | Номер систематичної вибірки ( |
| |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| I II III IV | 0 6 18 26 | 1 8 19 30 | 1 9 20 31 | 2 10 20 31 | 5 13 24 33 | 4 12 23 32 | 7 15 25 35 | 7 16 28 37 | 8 16 29 38 | 6 17 27 38 | 4,1 12,2 23,3 33,1 |
|
| 12, 5 | 14, 75 | 15, 25 | 15, 75 | 18, 75 | 17, 75 | 20, 5 | 22 | 22, 75 | 22 | 72,7 |
|
| 50 | 58 | 61 | 63 | 75 | 71 | 82 | 88 | 91 | 88 | |
Середнє значення систематичної вибірки має розподіл
![]() ~
~ 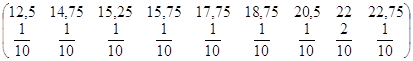
![]()
![]()
Дисперсія систематичної вибірки дорівнює
![]()
Знайдемо середнє та дисперсію для всієї популяції:
![]()
![]()
Тепер знайдемо дисперсію одиниць, що належать до однієї й тієї самої страти:
![]() ,
,
де ![]() - число страт,
- число страт, ![]() - обсяг стратифікованої вибірки.
- обсяг стратифікованої вибірки.
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
![]() ,
,
де ![]() - обсяг простої випадкової вибірки.
- обсяг простої випадкової вибірки.
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
![]() ,
,
де ![]() - число страт.
- число страт.
Стратифікований випадковий відбір та систематичний відбір виявились набагато ефективнішими, ніж простий випадковий відбір, причому, як і очікувалось, систематичний відбір менш точний, ніж стратифікований випадковий відбір.
Похожие работы
... ірювання; 6) обчислення довірчої випадкової похибки і загальної похибки результату опосередкованого вимірювання; при нелінійній залежності знаходять систематичну похибку опосередкованих вимірювань, обумовлену перехресними членами у рівнянні. При прямих одноразових вимірюваннях початкових величин процедура визначення результату Y опосередкованих вимірювань зберігається такою самою, як і при ...
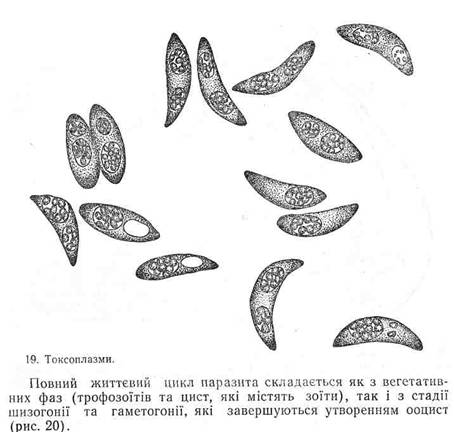
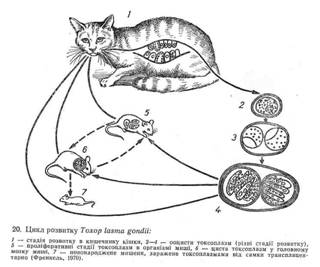
... . Приміщення механічно очищають і знезаражують 5-процетним розчином формальдегіду або 3-процентним розчином лізолу. М'ясо, шкурки і пух хворих кролів ніяким обмеженням не підлягають. Токсоплазмоз. Кролі, як і інші ссавці, сприйнятливі до токсоплазмозу. Хворі на цю хворобу кролі можуть бути джерелом зараження людини і тварин. Етіологія. Збудник — Toxoplasma gondii має форму півмісяця і нагадує ...
... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується методика розробки ефективних критеріїв оцінки інноваційних ...
... є грубим. 2.8. Методи вилучення систематичних похибок з результатів вимірювань Систематичні похибки, незалежно від характеру їх змінювання в часі при постановці і проведенні вимірювального експерименту, повинні бути виявлені і вилучені з результатів вимірювань або хоча б зменшені, для чого важливо знати джерела і причини їх виникнення. За цією ознакою розрізняють такі систематичні похибки: ...




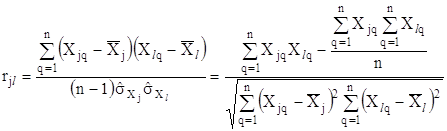
0 комментариев