Навигация
Місто StatVillage
2.1 Місто StatVillage
StatVillage – це гіпотетичне місто, яке складається з окремих домогосподарств і використовується як база даних для студентів та аспірантів, що вивчають вибіркові методи.
Дані домогосподарств для StatVillage обирались навмання з результатів перепису сімей, що мешкали в домогосподарствах у місті Ванкувері, Британській Колумбії, Канаді у 1991 році. Сам перепис населення проходив шляхом анонімного анкетування. Бралися до уваги наступні характеристики:
· демографічні показники – розмір домогосподарства та його склад за віком та статтю;
· показники доходу – зайнятість, інвестиції, валові витрати, різні доходи домогосподарств та інші;
· житлові характеристики – тип житла, рік побудови, своє житло чи орендоване, оціночна вартість, щомісячні витрати на розміщення та інші;
· характеристика двох головних членів сім’ї, які відповідають за добробут сім’ї – вік, стать, професія, рідна мова, освіта, зайнятість і т.д;
Існують три конфігурації міста StatVillage:
· Maximal village – складається зі 128 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств - 1024).
· Mini village – складається з 60 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств – 480).
· Micro village – складається з 36 блоків, кожен з яких містить 8 домогосподарств (загальна кількість домогосподарств – 288).
Кожен блок домогосподарств нумерується в певному порядку, а саме
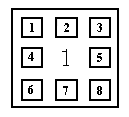
Рис. 2.1.1 Нумерування блоку домогосподарств
Для того, щоб отримати дані з міста StatVillage, необхідно спочатку відмітити домогосподарства позначкою як показано на рисунку 2.1.2 (відмічено кожне 8-ме домогосподарство)

Рис. 2.1.2 Систематичної вибірка кожного восьмого домогосподарства
Після цього натискаємо кнопку «Get the sample units» і отримуємо код, який представлений на рис. 2.1.3
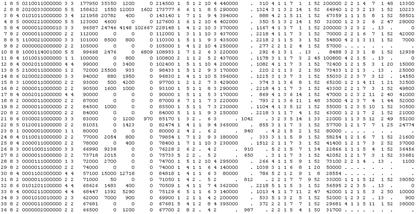
Рис. 2.1.3 Код отриманої вибірки
Отриманий код містить 36 стовбців, кожен з яких відповідає за окрему характеристику домогосподарства. Розшифровка коду наведена в додатку А.
2.2 Порівняння відборів
В своїй роботі я використовую другу конфігурацією StatVillage, а саме Mini Village, яка складається з 60-ти блоків. Для того, щоб порівняти точності систематичного, простого випадкового та стратифікованого відборів, я буду використовувати вибірки, добуті з 11-го та 13-го стовпців коду. Ці стовпці називаються TOTINCH та BUILTH, що є загальним доходом домогосподарства (включає в себе заробітну плату, пенсії, дівіденти та відсотки за депозитами і т.д.) та періодом побудови домогосподарства відповідно.
В результаті дослідження виявилось, що домогосподарства в StatVillage впорядковані за загальним доходом, а саме загальний дохід зменшується зі зростанням номеру домогосподарства. Логарифмічна регресія значуща. На рисунку 2.2.1 представлена діаграма розсіювання та логарифмічна регресія.
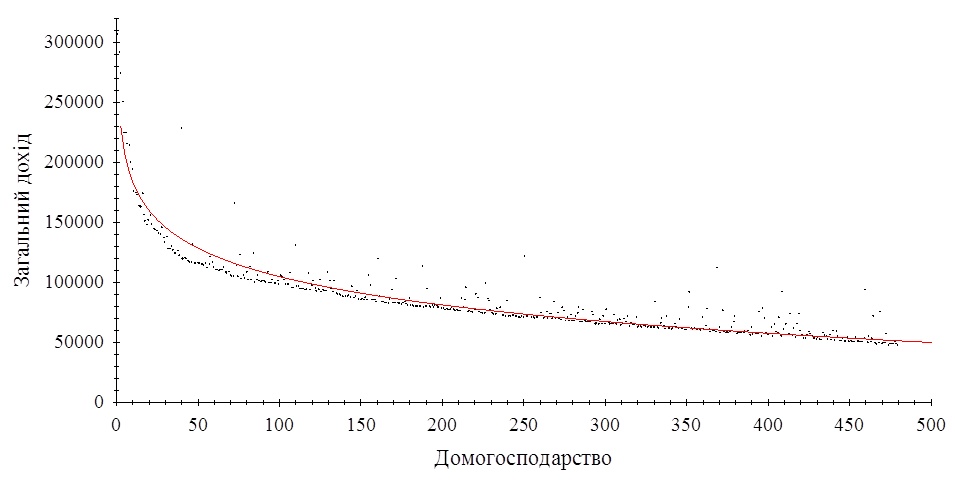 Рис. 2.2.1 Діаграма розсіювання
Рис. 2.2.1 Діаграма розсіювання
Рівняння регресії: ![]() F-статистика:
F-статистика: ![]() Логарифмічна регресія значуща.
Логарифмічна регресія значуща.
Порівняємо дисперсії середнього доходу домогосподарств при систематичному відборі кожного восьмого домогосподарства, простому випадковому відборі та стратифікованому відборі. Після отримання коду з 11-го стовпця (див. рис 2.1.3) запишемо дані в таблицю 2.2.1, розділивши на 60 страт.
Таблиця 2.2.1 Дані по 8-ми систематичним вибіркам
| Страта | Номер систематичної вибірки (k=8) |
| |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 214500 | 306000 | 291178 | 274200 | 250000 | 224230 | 224308 | 215448 | 249983 |
| 2 | 173777 | 200000 | 194322 | 175879 | 175000 | 173058 | 163673 | 162425 | 177266,8 |
| 3 | 143140 | 156667 | 150750 | 148433 | 151774 | 155215 | 147700 | 144781 | 149807,5 |
| 4 | 127600 | 142800 | 140900 | 140000 | 145148 | 137400 | 132998 | 137526 | 138046,5 |
| 5 | 228148 | 127706 | 129400 | 127109 | 124365 | 124324 | 126280 | 122300 | 138704 |
| 6 | 116200 | 120000 | 120393 | 120021 | 117561 | 116876 | 116400 | 131253 | 119838 |
| 7 | 112000 | 116000 | 116000 | 116000 | 115000 | 115400 | 114497 | 115936 | 115104,1 |
| 8 | 110300 | 114766 | 121294 | 117000 | 112100 | 110000 | 110000 | 109600 | 113132,5 |
| 9 | 105000 | 110830 | 112144 | 108481 | 108000 | 108601 | 105493 | 105000 | 107943,6 |
| 10 | 108953 | 165544 | 114427 | 105200 | 122916 | 102865 | 105664 | 102900 | 116058,6 |
| 11 | 100800 | 102400 | 113340 | 101800 | 124400 | 100702 | 102567 | 105400 | 106426,1 |
| 12 | 102400 | 100400 | 101300 | 101000 | 100333 | 108470 | 99070 | 99800 | 101596,6 |
| 13 | 98433 | 99400 | 98957 | 100871 | 98719 | 105833 | 104889 | 101700 | 101100,3 |
| 14 | 96830 | 98100 | 98000 | 107589 | 96050 | 96000 | 130797 | 96193 | 102444,9 |
| 15 | 97700 | 94728 | 94600 | 94542 | 93929 | 93728 | 107275 | 93933 | 96304,38 |
| 16 | 93100 | 100850 | 95029 | 93000 | 93626 | 101800 | 92312 | 93610 | 95415,88 |
| 17 | 90000 | 93082 | 108632 | 101221 | 94304 | 92100 | 101150 | 90800 | 96411,13 |
| 18 | 87000 | 90000 | 88846 | 88697 | 92593 | 88400 | 88000 | 88800 | 89042 |
| 19 | 85500 | 96348 | 87483 | 88615 | 92728 | 86028 | 86000 | 86257 | 88619,88 |
| 20 | 84000 | 87073 | 85320 | 105548 | 97503 | 85800 | 85691 | 85120 | 89506,88 |
| 21 | 85170 | 120000 | 87893 | 83514 | 84134 | 83201 | 83080 | 83000 | 88749 |
| 22 | 82474 | 93489 | 82720 | 82530 | 102614 | 82800 | 82986 | 82080 | 86461,63 |
| 23 | 80000 | 84000 | 81777 | 80539 | 86759 | 81200 | 80800 | 80000 | 81884,38 |
| 24 | 79854 | 80000 | 80400 | 80000 | 113400 | 79350 | 80050 | 94375 | 85928,63 |
| 25 | 78400 | 79000 | 81268 | 79400 | 80800 | 79800 | 79532 | 86117 | 80539,63 |
| 26 | 76228 | 78075 | 77600 | 77985 | 77650 | 77359 | 79122 | 77096 | 77639,38 |
| 27 | 75733 | 77000 | 76149 | 76000 | 86069 | 78974 | 85351 | 95990 | 81408,25 |
| 28 | 74700 | 76400 | 75853 | 75000 | 76983 | 90305 | 87022 | 75528 | 78973,88 |
| 29 | 74000 | 74946 | 74961 | 99015 | 86590 | 84569 | 77300 | 74800 | 80772,63 |
| 30 | 84818 | 73587 | 77909 | 75210 | 79193 | 72400 | 73000 | 72110 | 76028,38 |
| 31 | 71050 | 72093 | 72200 | 72800 | 72800 | 71856 | 72174 | 71238 | 72026,38 |
| 32 | 70509 | 71400 | 71000 | 121762 | 71647 | 71397 | 72458 | 70750 | 77615,38 |
| 33 | 75129 | 70000 | 70800 | 70400 | 87400 | 74915 | 70000 | 70800 | 73680,5 |
| 34 | 69900 | 69731 | 73282 | 73792 | 69470 | 83568 | 69833 | 74300 | 72984,5 |
| 35 | 67681 | 69105 | 79079 | 76779 | 68550 | 71178 | 68033 | 72400 | 71600,63 |
| 36 | 67700 | 68400 | 71570 | 74400 | 78843 | 67400 | 67000 | 77141 | 71556,75 |
| 37 | 65659 | 66703 | 67217 | 66800 | 75000 | 72439 | 65400 | 66132 | 68168,75 |
| 38 | 65000 | 69320 | 65000 | 71800 | 65000 | 76890 | 66154 | 65500 | 68083 |
| 39 | 69600 | 65300 | 73111 | 65065 | 68457 | 69200 | 64400 | 65229 | 67545,25 |
| 40 | 63000 | 67200 | 71943 | 63652 | 66020 | 64400 | 63993 | 70740 | 66368,5 |
| 41 | 62900 | 63800 | 63800 | 62893 | 63200 | 63200 | 62697 | 63306 | 63224,5 |
| 42 | 63519 | 62500 | 62763 | 83643 | 62400 | 62095 | 65900 | 69725 | 66568,13 |
| 43 | 62364 | 61611 | 71443 | 61304 | 61300 | 61200 | 61908 | 65000 | 63266,25 |
| 44 | 92240 | 61400 | 68700 | 61355 | 61623 | 60468 | 61151 | 79534 | 68308,88 |
| 45 | 71233 | 61612 | 60800 | 61800 | 62000 | 60800 | 60910 | 60000 | 62394,38 |
| 46 | 58988 | 60374 | 63684 | 78065 | 60733 | 59000 | 59400 | 59400 | 62455,5 |
| 47 | 58400 | 111951 | 62227 | 58224 | 76761 | 58975 | 58000 | 58450 | 67873,5 |
| 48 | 57800 | 58500 | 62910 | 66981 | 71500 | 57400 | 57600 | 57800 | 61311,38 |
| 49 | 58354 | 57800 | 58871 | 58544 | 60217 | 56358 | 62763 | 57060 | 58745,88 |
| 50 | 55900 | 56800 | 57467 | 75196 | 55479 | 78122 | 69699 | 57527 | 63273,75 |
| 51 | 55350 | 56685 | 62369 | 55000 | 65300 | 59148 | 58400 | 71000 | 60406,5 |
| 52 | 61671 | 91516 | 61052 | 65277 | 56550 | 56850 | 73512 | 56000 | 65303,5 |
| 53 | 56467 | 54000 | 65700 | 73998 | 59781 | 55788 | 53530 | 53000 | 59033 |
| 54 | 52191 | 58700 | 57219 | 55441 | 53533 | 53300 | 52163 | 53879 | 54553,25 |
| 55 | 59391 | 52621 | 58086 | 55800 | 55500 | 52475 | 55818 | 52335 | 55253,25 |
| 56 | 51000 | 51713 | 59277 | 55347 | 51333 | 51600 | 53465 | 51857 | 53199 |
| 57 | 50527 | 54560 | 51000 | 51857 | 50859 | 50800 | 54540 | 50700 | 51855,38 |
| 58 | 53475 | 50500 | 50460 | 53426 | 93669 | 50000 | 55000 | 50800 | 57166,25 |
| 59 | 49517 | 71853 | 49400 | 49000 | 49214 | 75349 | 48594 | 49582 | 55313,63 |
| 60 | 47900 | 57499 | 48000 | 48992 | 48360 | 48400 | 50649 | 49105 | 49863,13 |
|
| 83852,88 | 88407,3 | 86154,58 | 86896,53 | 87045,67 | 83855,98 | 83469,18 | 83002,8 | 5120137 |
|
| 5031173 | 5304438 | 5169275 | 5213792 | 5222740 | 5031359 | 5008151 | 4980168 | |
У кожній страті міститься 1 блок, тобто 8 домогосподарств.
Знайдемо середнє та дисперсію для всієї популяції:
![]()
![]()
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
![]() .
.
Середнє значення систематичної вибірки має розподіл
![]() ~
~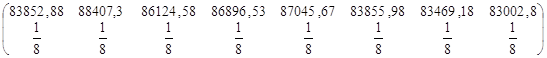
![]()
Оцінка ![]() є незміщеною оцінкою для
є незміщеною оцінкою для ![]() , дійсно
, дійсно ![]() .
.
![]()
Дисперсія систематичної вибірки дорівнює
![]()
Тепер знайдемо дисперсію одиниць, що належать до однієї і тієї самої страти:
![]()
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
![]() .
.
Отже, ми отримали такі результати:
![]()
![]()
![]() .
.
Це означає, що
![]() .
.
При наявності логарифмічної залежності між загальним доходом та номером домогосподарства систематичний відбір виявився точнішим за простий випадковий та стратифікований відбори.
Тепер розглянемо дані, в яких відсутній тренд. Використовуємо вибірки, добуті з 13-го стовпця коду. Цей стовбець має назву BUILTH і відповідає за період побудови домогосподарства.
В результаті дослідження даної вибірки, виявилось, що залежність між періодом побудови та номером домогосподарства відсутня. Лінійна регресія не значуща. На рисунку 2.2.2 представлена діаграма розсіювання та відсутність лінійної регресії.
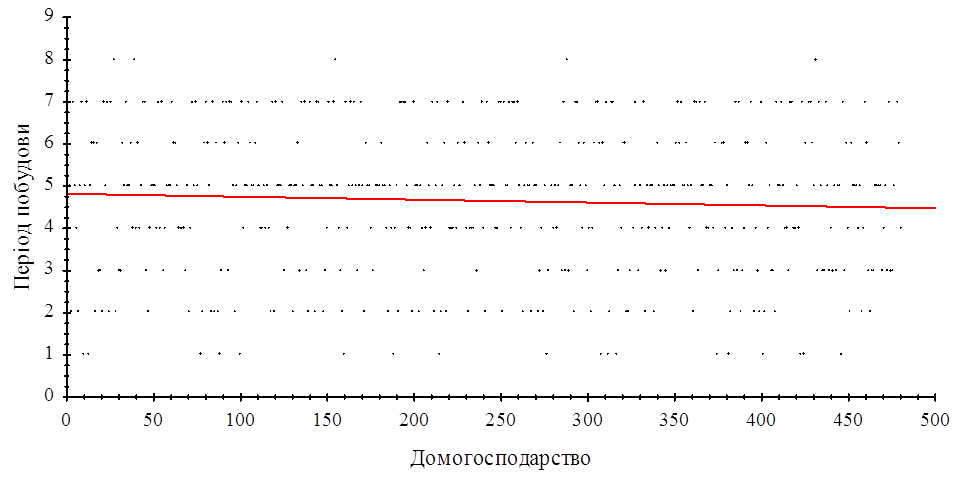 Рис. 2.2.2 Діаграма розсіювання
Рис. 2.2.2 Діаграма розсіювання
Рівняння регресії: ![]() F-статистика:
F-статистика: ![]() Лінійна регресія не значуща
Лінійна регресія не значуща
Порівняємо дисперсії середнього періоду побудови домогосподарства при систематичному відборі кожного восьмого домогосподарства, простому випадковому відборі та стратифікованому відборі. Після отримання коду з 13-го стовпця (див. рис 2.1.3) запишемо дані в таблицю 2.2.2, розділивши на 60 страт.
Таблиця 2.2.2 Дані по 8-ми систематичним вибіркам
| Страта | Номер систематичної вибірки (k=8) |
| |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 5 | 7 | 5 | 2 | 7 | 5 | 4 | 2 | 4,625 |
| 2 | 6 | 7 | 1 | 5 | 7 | 1 | 5 | 6 | 4,75 |
| 3 | 7 | 2 | 6 | 3 | 3 | 2 | 7 | 5 | 4,375 |
| 4 | 6 | 2 | 7 | 8 | 2 | 4 | 3 | 3 | 4,375 |
| 5 | 4 | 5 | 7 | 5 | 5 | 6 | 4 | 8 | 5,5 |
| 6 | 4 | 6 | 4 | 5 | 7 | 7 | 3 | 2 | 4,75 |
| 7 | 3 | 5 | 5 | 5 | 4 | 7 | 4 | 7 | 5 |
| 8 | 5 | 4 | 5 | 5 | 5 | 7 | 6 | 6 | 5,375 |
| 9 | 4 | 4 | 4 | 4 | 4 | 3 | 5 | 2 | 3,75 |
| 10 | 7 | 7 | 5 | 7 | 5 | 1 | 2 | 6 | 5 |
| 11 | 1 | 6 | 5 | 2 | 7 | 2 | 6 | 2 | 3,875 |
| 12 | 5 | 3 | 7 | 6 | 7 | 3 | 7 | 7 | 5,625 |
| 13 | 5 | 2 | 5 | 6 | 1 | 7 | 4 | 5 | 4,375 |
| 14 | 4 | 7 | 6 | 5 | 5 | 6 | 7 | 5 | 5,625 |
| 15 | 2 | 4 | 5 | 4 | 5 | 4 | 2 | 7 | 4,125 |
| 16 | 5 | 7 | 5 | 5 | 5 | 7 | 3 | 4 | 5,125 |
| 17 | 5 | 5 | 2 | 5 | 5 | 6 | 3 | 7 | 4,75 |
| 18 | 7 | 7 | 3 | 2 | 7 | 5 | 5 | 2 | 4,75 |
| 19 | 5 | 7 | 5 | 5 | 2 | 3 | 4 | 7 | 4,75 |
| 20 | 1 | 5 | 7 | 8 | 5 | 4 | 3 | 2 | 4,375 |
| 21 | 3 | 7 | 4 | 5 | 7 | 5 | 7 | 5 | 5,375 |
| 22 | 4 | 5 | 7 | 5 | 2 | 6 | 5 | 5 | 4,875 |
| 23 | 4 | 3 | 5 | 5 | 5 | 6 | 5 | 5 | 4,75 |
| 24 | 7 | 2 | 5 | 4 | 1 | 4 | 5 | 2 | 3,75 |
| 25 | 7 | 7 | 7 | 7 | 5 | 4 | 4 | 2 | 5,375 |
| 26 | 6 | 5 | 5 | 2 | 5 | 4 | 3 | 4 | 4,25 |
| 27 | 2 | 5 | 4 | 7 | 2 | 5 | 7 | 1 | 4,125 |
| 28 | 5 | 5 | 6 | 2 | 7 | 4 | 4 | 4 | 4,625 |
| 29 | 4 | 4 | 6 | 5 | 7 | 6 | 4 | 2 | 4,75 |
| 30 | 4 | 4 | 4 | 5 | 3 | 6 | 5 | 7 | 4,75 |
| 31 | 4 | 2 | 7 | 6 | 5 | 5 | 5 | 4 | 4,75 |
| 32 | 4 | 7 | 7 | 2 | 7 | 5 | 5 | 7 | 5,5 |
| 33 | 5 | 7 | 7 | 6 | 7 | 5 | 4 | 2 | 5,375 |
| 34 | 2 | 6 | 5 | 5 | 2 | 6 | 5 | 5 | 4,5 |
| 35 | 4 | 3 | 4 | 2 | 5 | 1 | 3 | 5 | 3,375 |
| 36 | 8 | 5 | 4 | 5 | 6 | 3 | 7 | 3 | 5,125 |
| 37 | 5 | 3 | 5 | 5 | 2 | 7 | 7 | 6 | 5 |
| 38 | 6 | 4 | 6 | 5 | 3 | 4 | 2 | 4 | 4,25 |
| 39 | 1 | 7 | 7 | 6 | 1 | 6 | 5 | 7 | 5 |
| 40 | 4 | 2 | 7 | 7 | 5 | 1 | 3 | 5 | 4,25 |
| 41 | 7 | 6 | 6 | 2 | 2 | 3 | 4 | 5 | 4,375 |
| 42 | 5 | 3 | 5 | 4 | 7 | 2 | 5 | 4 | 4,375 |
| 43 | 5 | 5 | 2 | 4 | 6 | 5 | 3 | 4 | 4,25 |
| 44 | 7 | 3 | 5 | 4 | 5 | 5 | 5 | 6 | 5 |
| 45 | 5 | 6 | 7 | 5 | 5 | 6 | 5 | 4 | 5,375 |
| 46 | 7 | 2 | 7 | 7 | 3 | 7 | 5 | 5 | 5,375 |
| 47 | 3 | 4 | 4 | 5 | 5 | 4 | 6 | 1 | 4 |
| 48 | 3 | 6 | 6 | 4 | 5 | 1 | 2 | 4 | 3,875 |
| 49 | 6 | 7 | 3 | 7 | 2 | 3 | 4 | 6 | 4,75 |
| 50 | 7 | 5 | 7 | 5 | 2 | 4 | 3 | 2 | 4,375 |
| 51 | 2 | 1 | 2 | 6 | 4 | 5 | 3 | 3 | 3,25 |
| 52 | 3 | 7 | 5 | 5 | 7 | 5 | 4 | 4 | 5 |
| 53 | 7 | 7 | 7 | 4 | 4 | 5 | 4 | 1 | 4,875 |
| 54 | 3 | 1 | 6 | 7 | 7 | 6 | 5 | 8 | 5,375 |
| 55 | 4 | 7 | 5 | 3 | 3 | 7 | 5 | 3 | 4,625 |
| 56 | 3 | 3 | 5 | 3 | 5 | 5 | 1 | 7 | 4 |
| 57 | 4 | 6 | 4 | 2 | 6 | 5 | 5 | 5 | 4,625 |
| 58 | 3 | 5 | 2 | 4 | 7 | 6 | 3 | 2 | 4 |
| 59 | 5 | 3 | 5 | 5 | 5 | 5 | 3 | 4 | 4,375 |
| 60 | 4 | 3 | 7 | 3 | 3 | 5 | 7 | 6 | 4,75 |
|
| 4,55 | 4,75 | 5,18 | 4,7 | 4,63 | 4,62 | 4,4 | 4,4 | 279,25 |
|
| 273 | 285 | 311 | 282 | 278 | 277 | 264 | 264 | |
Знайдемо середнє та дисперсію для всієї популяції:
![]()
![]()
Тоді дисперсія оцінки середнього для простої випадкової вибірки має вид:
![]() .
.
Середнє значення систематичної вибірки має розподіл
![]() ~
~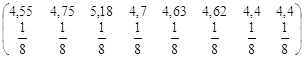
![]()
Також отримали, що ![]() .
.
![]()
Дисперсія систематичної вибірки дорівнює
![]()
Тепер знайдемо дисперсію одиниць, що належать до однієї і тієї самої страти:
![]()
Дисперсія оцінки середнього для стратифікованої випадкової вибірки
![]() .
.
Отже, ми отримали такі результати:
![]()
![]()
![]() .
.
Це означає, що
![]() .
.
При відсутності тренду систематичний відбір виявився ефективнішим ніж стратифікований відбір, але менш точним ніж простий випадковий відбір. Якщо порівняти дисперсії систематичної та простої випадкової вибірок, то виявиться що вони дуже мало відрізняються. При випадковому порядку розміщення одиниць систематичний відбір в середньому рівносильний простому випадковому відбору (останнє підтверджує теоретичні положення підрозділу 1.3).
Для підвищення точності систематичного відбору, при дослідженні періоду побудови домогосподарства, застосуємо стратифікований систематичний відбір. Основна його ідея розглядалась у підрозділі 1.9. Отже, всю популяцію, яка складається з 60-ти блоків (по 8 домогосподарств у кожному), ділимо на 2 страти. В першій страті розміщуються з 1-го по 32-й блоки (тобто 256 домогосподарств), а в другій – з 33-го по 60-й блоки (224 домогосподарства). З кожної страти здобуваємо систематичні вибірки кожної 8-ї одиниці. Всього комбінацій здобуття таких систематичних вибірок з двох страт – 64 (8 комбінацій з першої страти та 8 – з другої страти). Середнє значення стратифікованої систематичної вибірки рахується за формулою
![]() ,
,
де ![]() - це вага страти
- це вага страти ![]() , а
, а ![]() - середнє значення систематичної вибірки у страті
- середнє значення систематичної вибірки у страті ![]() .
.
Так як я буду розглядати 2 страти, то середнє значення стратифікованої систематичної вибірки має вигляд:
![]()
![]()
![]()
а ![]() для кожної систематичної вибірки у першій або другій страті своє.
для кожної систематичної вибірки у першій або другій страті своє.
Після розглядання всіх стратифікованих систематичних вибірок кожної 8-ї одиниці запишемо розподіл ![]() :
:
![]()
![]()
![]()
Також має місце рівність ![]() .
.
![]()
Дисперсія середнього стратифікованої систематичної вибірки дорівнює:
![]() .
.
При застосуванні стратифікованого систематичного відбору для періоду побудови домогосподарства маємо наступні результати:
![]()
![]()
![]() .
.
Це означає, що
![]() .
.
При відсутності тренду стратифікований систематичний відбір є точнішим за простий випадковий та стратифікований відбори. Тобто стратифікований систематичний відбір дає більш точну оцінку ніж звичайний систематичний відбір.
Висновки
Вибірковий метод – метод дослідження, що дозволяє робити висновок про характер розподілу досліджуваних ознак популяції на основі розгляду деякої її частини (тобто вибірки). Прикладом вибіркових обстежень може бути визначення середнього рівня доходів населення, визначення переліку споживчих переваг, визначення рейтингу кандидата на виборах та інші. Існують різні методи вибіркового обстеження: простий випадковий відбір, стратифікований відбір, систематичний відбір, кластерний та інші. Для різних популяцій різні методи відбору можуть бути більш точними або менш точними.
Розглянемо простий, систематичний та стратифікований відбори. Простим випадковим відбором називається спосіб добування ![]() одиниць вибірки з
одиниць вибірки з ![]() одиниць популяції так, що кожна з
одиниць популяції так, що кожна з ![]() вибірок має рівну імовірність бути відібраною. За допомогою таблиці або датчика випадкових чисел добуваємо вибірку обсягом
вибірок має рівну імовірність бути відібраною. За допомогою таблиці або датчика випадкових чисел добуваємо вибірку обсягом ![]() .
.
Систематичний відбір полягає у тому, що з популяції, одиниці якої перенумеровані від 1 до ![]() , для здобуття вибірки обсягу
, для здобуття вибірки обсягу ![]() спочатку навмання вибираємо будь-яку одиницю з перших
спочатку навмання вибираємо будь-яку одиницю з перших ![]() одиниць популяції (наприклад, п’яту одиницю з 8-ми одиниць). Після вибору першої одиниці вибираємо кожну
одиниць популяції (наприклад, п’яту одиницю з 8-ми одиниць). Після вибору першої одиниці вибираємо кожну ![]() -ту одиницю популяції (тобто 10-ту, 15-ту, 20-ту, 25-ту,….,
-ту одиницю популяції (тобто 10-ту, 15-ту, 20-ту, 25-ту,….,![]() -ту). Таку вибірку називають систематичною вибіркою кожної
-ту). Таку вибірку називають систематичною вибіркою кожної ![]() -ї одиниці.
-ї одиниці.
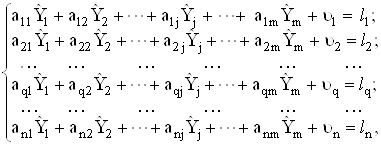
Стратифікований відбір полягає в тому, що вся популяція поділяється на менші під популяції (страти), які не мають спільних одиниць і кожна з яких внутрішньо однорідна. Потім за допомогою простого випадкового відбору з кожної страти здобувається вибірка. Такий відбір називається стратифікованим випадковим відбором. Наприклад, популяція з ![]() одиниць поділена на
одиниць поділена на ![]() страт, по 8 одиниць у кожній страті. З кожної страти здобуваємо по 2 одиниці за допомогою таблиці або датчика випадкових чисел. В результаті отримаємо: в першій страті числа 2, 7; в другій страті - 13, 16; і т.д.
страт, по 8 одиниць у кожній страті. З кожної страти здобуваємо по 2 одиниці за допомогою таблиці або датчика випадкових чисел. В результаті отримаємо: в першій страті числа 2, 7; в другій страті - 13, 16; і т.д.
В роботі ставиться задача порівняння точності систематичного відбору, простого випадкового та стратифікованого відбору.
Для розв’язання цієї задачі використано наступні теоретичні положення.
1. Середнє значення ![]() систематичної вибірки є незміщеною оцінкою для середнього значення популяції
систематичної вибірки є незміщеною оцінкою для середнього значення популяції ![]() .
.
![]() (1)
(1)
2. Дисперсія середнього значення систематичної вибірки визначається формулою (2)
![]() (2)
(2)
де дисперсія одиниць, які належать одній систематичній вибірці визначається формулою (3),
![]() (3)
(3)
а дисперсія популяції визначається формулою (4)
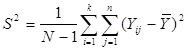 (4)
(4)
3. Середнє значення для систематичної вибірки більш точне, ніж середнє для простої випадкової вибірки
![]()
тоді і тільки тоді, коли справедлива нерівність (5)
![]() . (5)
. (5)
Похожие работы
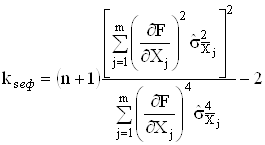
... ірювання; 6) обчислення довірчої випадкової похибки і загальної похибки результату опосередкованого вимірювання; при нелінійній залежності знаходять систематичну похибку опосередкованих вимірювань, обумовлену перехресними членами у рівнянні. При прямих одноразових вимірюваннях початкових величин процедура визначення результату Y опосередкованих вимірювань зберігається такою самою, як і при ...
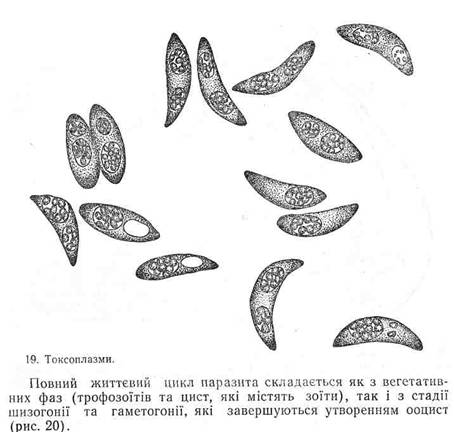
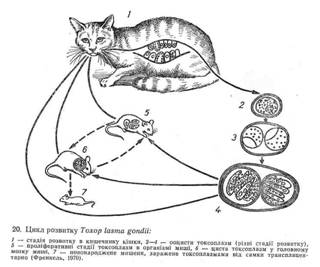
... . Приміщення механічно очищають і знезаражують 5-процетним розчином формальдегіду або 3-процентним розчином лізолу. М'ясо, шкурки і пух хворих кролів ніяким обмеженням не підлягають. Токсоплазмоз. Кролі, як і інші ссавці, сприйнятливі до токсоплазмозу. Хворі на цю хворобу кролі можуть бути джерелом зараження людини і тварин. Етіологія. Збудник — Toxoplasma gondii має форму півмісяця і нагадує ...
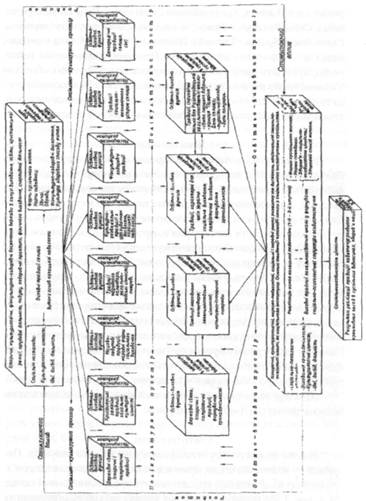
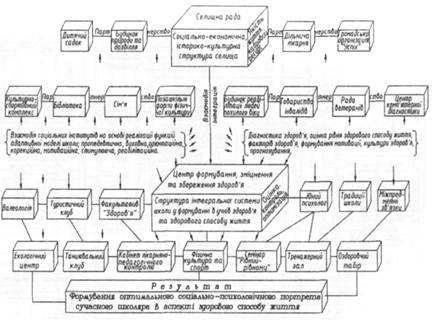
... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується методика розробки ефективних критеріїв оцінки інноваційних ...
... є грубим. 2.8. Методи вилучення систематичних похибок з результатів вимірювань Систематичні похибки, незалежно від характеру їх змінювання в часі при постановці і проведенні вимірювального експерименту, повинні бути виявлені і вилучені з результатів вимірювань або хоча б зменшені, для чого важливо знати джерела і причини їх виникнення. За цією ознакою розрізняють такі систематичні похибки: ...




0 комментариев