Оцінювання дисперсії за окремою вибіркою

1.8 Оцінювання дисперсії за окремою вибіркою

Згідно з результатами, які відносяться до простих випадкових вибірок з , ми можемо обчислити незміщену оцінку дисперсії вибіркового середнього, при цьому оцінка буде незміщеною незалежно від виду популяції. Але для систематичної вибірки ця корисна властивість не зберігається, оскільки її можна розглядати лише як просту випадкову вибірку з , тобто одним членом. Проілюструємо це на прикладі зі зміною «по синусоїді». Нехай

,

де (обираємо кожну четверту одиницю) та  Послідовними спостереженнями в популяції будуть

Якщо за перший член обрати значення , то всі члени систематичної вибірки мають значення . При трьох інших можливих значеннях першого члена всі вони приймають значення відповідно ,  або . Таким чином, за окремою вибіркою ми не можемо оцінити величину . В той час справжнє значення дисперсії вибіркового середнього систематичної вибірки дорівнює . Цей приклад ілюструє, що при існуванні періодичної варіації в популяції незміщену оцінку дисперсії по вибірці побудувати неможливо.

Але останнє не означає, що зовсім нічого не можна зробити. За виключенням випадку періодичної варіації, ми можемо користуватися інформацією про структуру популяції для того, щоб побудувати математичну модель, яка адекватно представляє існуючий в популяції тип варіації. Після цього ми могли б вивести формулу для оцінки дисперсії, яка для цієї моделі була б наближено незміщеною, хоча, можливо, для інших моделей зміщення було б великим. Вирішувати, яку з моделей необхідно застосовувати, повинен той, хто організовує спостереження.

Далі наведені без доведень деякі прості моделі з відповідними оцінками дисперсій.

Найбільш проста модель відноситься до популяції, в якій  містить деякий тренд плюс «випадковий» доданок. Тоді

,

де  − деяка функція . Відносно випадкового доданка  ми припускаємо, що існує надпопуляція, для якої

   .

Оцінка дисперсії  називається незміщеною оцінкою дисперсії , якщо

,

тобто, якщо вона незміщена відносно середнього по всім скінченим популяціям, які можуть бути отримані з цієї надпопуляції.

Популяція, одиниці якої розташовані навмання.

.

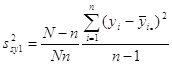Остання формула є оцінкою дисперсії систематичної вибірки - тої одиниці.

Ця модель застосовується, якщо ми впевненні в тому, що порядок розташування одиниць має в основному випадковий характер відносно ознаки, що спостерігається. Формула дисперсії збігається з формулою дисперсії простого випадкового відбору, і її оцінка незміщена, якщо наша модель справедлива.

Стратифікована популяція, одиниці якої у стратах розташовані навмання

.

В цьому випадку середнє значення є постійним всередині кожної страти з  одиниць. Оцінка , яка заснована на середньому квадраті послідовних різниць, не буде незміщеною. В її утворенні приймають небажану участь різниці значень  сусідніх страт і, зокрема, при оцінюванні випадкового доданку дисперсії перша та остання страти мають занадто малу вагу. Якщо наша модель справедлива, то для достатньо великих вибірок ця оцінка буде, взагалі кажучи, перевищувати дисперсію.

Лінійний тренд

.

Оцінка заснована на квадратах послідовних різниць, що утворюються трьома сусідніми значеннями , ,  у вибірці. Сума квадратів містить  членів. У випадку лінійного тренду його можна виключити, використовуючи кінцеві поправки. Член  дорівнює сумі квадратів ваг у виразі . Якщо тільки  не мале,  можна замінити звичайним множником . Це можна зробити, оскільки крайнім стратам надана дуже мала вага, оцінка зміщена, за виключенням випадку, коли  є постійною величиною. Але якщо  велике і наша модель справедлива, то оцінка буде цілком задовільною.

Похожие работы

Систематична похибка опосередкованих вимірювань

Скачать

16438

2

9

... ірювання; 6) обчислення довірчої випадкової похибки і загальної похибки результату опосередкованого вимірювання; при нелінійній залежності знаходять систематичну похибку опосередкованих вимірювань, обумовлену перехресними членами у рівнянні. При прямих одноразових вимірюваннях початкових величин  процедура визначення результату Y опосередкованих вимірювань зберігається такою самою, як і при ...

Хвороби кролів, спричинювані найпростішими з неясним систематичним положенням. Нематодози

Скачать

21146

0

5

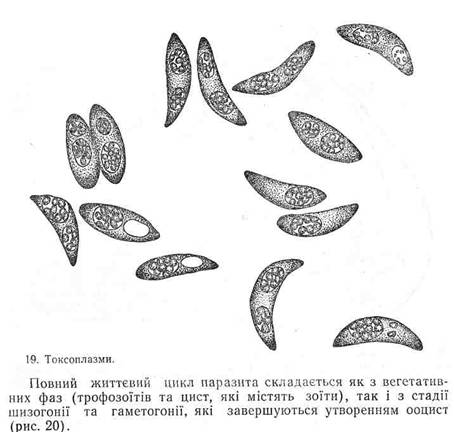
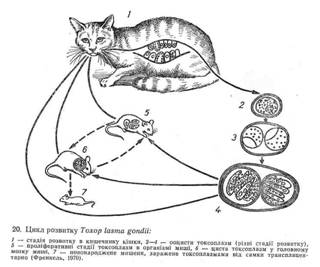
... . Приміщення механічно очищають і знезаражують 5-процетним розчином формальдегіду або 3-процентним розчином лізолу. М'ясо, шкурки і пух хворих кролів ніяким обмеженням не підлягають. Токсоплазмоз. Кролі, як і інші ссавці, сприйнятливі до токсоплазмозу. Хворі на цю хворобу кролі можуть бути джерелом зараження людини і тварин. Етіологія. Збудник — Toxoplasma gondii має форму півмісяця і нагадує ...

Взаємодія соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків

Скачать

664560

27

18

... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується ме­тодика розробки ефективних критеріїв оцінки інноваційних ...

Виявлення грубих результатів вимірювань

Скачать

25191

2

2

... є грубим. 2.8. Методи вилучення систематичних похибок з результатів вимірювань   Систематичні похибки, незалежно від характеру їх змінювання в часі при постановці і проведенні вимірювального експерименту, повинні бути виявлені і вилучені з результатів вимірювань або хоча б зменшені, для чого важливо знати джерела і причини їх виникнення. За цією ознакою розрізняють такі систематичні похибки: ...