Навигация
Второй вариант метода «переноса краевых условий» в произвольную точку интервала интегрирования
5 Второй вариант метода «переноса краевых условий» в произвольную точку интервала интегрирования
Этот вариант метода еще не обсчитан на компьютерах.
Предложено выполнять интегрирование по формулам теории матриц [Гантмахер] сразу от некоторой внутренней точки интервала интегрирования к краям:
Y(0) = K(0←x) ∙ Y(x) + Y*(0←x) ,
Y(1) = K(1←x) ∙ Y(x) + Y*(1←x) .
Подставим эти формулы в краевые условия и получим:
U∙Y(0) = u,
U∙[ K(0←x) ∙ Y(x) + Y*(0←x) ] = u,
[ U∙ K(0←x) ] ∙ Y(x) = u - U∙Y*(0←x) .
и
V∙Y(1) = v,
V∙[ K(1←x) ∙ Y(x) + Y*(1←x) ] = v,
[ V∙ K(1←x) ] ∙ Y(x) = v - V∙Y*(1←x) .
То есть получаем два матричных уравнения краевых условий, перенесенные в рассматриваемую точку x:
[ U∙ K(0←x) ] ∙ Y(x) = u - U∙Y*(0←x) ,
[ V∙ K(1←x) ] ∙ Y(x) = v - V∙Y*(1←x) .
Эти уравнения аналогично объединяются в одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения решения Y(x) в любой рассматриваемой точке x:
![]() ∙ Y(x) =
∙ Y(x) = 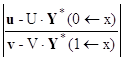 .
.
В случае «жестких» дифференциальных уравнений предлагается следующий алгоритм.
Используем свойство перемножаемости матриц Коши:
K(x![]() ←x) = K(x
←x) = K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ … ∙ K(x
) ∙ … ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x)
←x)
и запишем выражения для матриц Коши, например, в виде:
K(0←x) = K(0←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x),
←x),
K(1←x) = K(1←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x),
←x),
Тогда перенесенные краевые условия можно записать в виде:
[ U∙ K(0←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x) ] ∙ Y(x) = u - U∙Y*(0←x) ,
←x) ] ∙ Y(x) = u - U∙Y*(0←x) ,
[ V∙ K(1←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x) ] ∙ Y(x) = v - V∙Y*(1←x)
←x) ] ∙ Y(x) = v - V∙Y*(1←x)
или в виде:
[ U∙ K(0←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x) ] ∙ Y(x) = u* ,
←x) ] ∙ Y(x) = u* ,
[ V∙ K(1←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x) ] ∙ Y(x) = v* .
←x) ] ∙ Y(x) = v* .
Тогда рассмотрим левое перенесенное краевое условие:
[ U∙ K(0←x![]() ) ∙ K(x
) ∙ K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x) ] ∙ Y(x) = u* ,
←x) ] ∙ Y(x) = u* ,
[ U∙ K(0←x![]() ) ] ∙ { K(x
) ] ∙ { K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x) ∙ Y(x) } = u* ,
←x) ∙ Y(x) } = u* ,
[ матрица ] ∙ { вектор } = вектор .
Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[ U∙ K(0←x![]() ) ]
) ]![]() ∙ { K(x
∙ { K(x![]() ←x
←x![]() ) ∙ K(x
) ∙ K(x![]() ←x) ∙ Y(x) } = u*
←x) ∙ Y(x) } = u*![]() .
.
Далее последовательно можно записать:
[[ U∙ K(0←x![]() ) ]
) ]![]() ∙
K(x
∙
K(x![]() ←x
←x![]() ) ] ∙ { K(x
) ] ∙ { K(x![]() ←x) ∙ Y(x) } = u*
←x) ∙ Y(x) } = u*![]() ,
,
[ матрица ] ∙ { вектор } = вектор .
Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[[ U∙ K(0←x![]() ) ]
) ]![]() ∙
K(x
∙
K(x![]() ←x
←x![]() ) ]
) ] ![]() ∙ { K(x
∙ { K(x![]() ←x) ∙ Y(x) } = u*
←x) ∙ Y(x) } = u*![]() ,
,
Далее аналогично можно записать:
[[[ U∙ K(0←x![]() ) ]
) ]![]() ∙
K(x
∙
K(x![]() ←x
←x![]() ) ]
) ] ![]() ∙ K(x
∙ K(x![]() ←x) ] ∙ { Y(x) } = u*
←x) ] ∙ { Y(x) } = u*![]() ,
,
[ матрица ] ∙ { вектор} = вектор .
Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[[[ U∙ K(0←x![]() ) ]
) ]![]() ∙ K(x
∙ K(x![]() ←x
←x![]() ) ]
) ] ![]() ∙ K(x
∙ K(x![]() ←x) ]
←x) ] ![]() ∙ Y(x) = u*
∙ Y(x) = u*![]() .
.
Аналогично можно проортонормировать матричное уравнение краевых условий и для правого края независимо от левого края.
Далее проортонормированные уравнения краевых условий:
[ U∙ K(0←x) ]![]() ∙ Y(x) = u*
∙ Y(x) = u*![]() ,
,
[ V∙ K(1←x) ]![]() ∙ Y(x) = v*
∙ Y(x) = v*![]()
как и ранее объединяются в одну обычную систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения искомого вектора Y(x) :
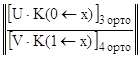 ∙ Y(x) =
∙ Y(x) = 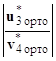 .
.
Похожие работы
... матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются: , где матрицы Коши приближенно вычисляются по формуле: , где . 2. Метод решения жестких краевых задач без ортонормирования – метод сопряжения участков, выраженных матричными экспонентами. Разделим интервал интегрирования краевой задачи, например, на 3 участка. Будем иметь точки (узлы), ...
... . 4. Какие основные факторы нужно определить прежде, чем формировать инвестиционный портфель клиента? 5. Опишите простую структуру инвестиционного портфеля. ВВЕДЕНИЕ РАЗВИТИЕ РЫНКА ЦЕННЫХ БУМАГ В РОССИИ И ЗАДАЧИ РЕГУЛИРОВАНИЯ Рынок ценных бумаг в России начал свое формирование в первой половине 1991 г. после принятия известного Постановления Совета министров РСФСР ¹ 601 от 25 ...
... . А организованная преступность ещё имеет причины общие с неорганизованной преступностью. 3.3 Методы борьбы с организованной преступностью.21 В основе предупреждения организованной преступности лежат общесоциальные и экономические меры.Прежде всего нужны эффективные законы, отвечающие характеру современной преступности. Сегодняшний уголовный закон ...
... на поздних стадиях начинают проявляться ряд факторов объективного, природного характера, осложняющие ситуацию в решении парафиновой проблемы и снижающие эффективность традиционных мероприятий. 3.3 Методы используемые в НГДУ “Нурлатнефть” по предотвращению отложений АСПО 3.3.1 Механические методы борьбы с АСПО и технология работ при их применении Группа механических методов борьбы с ...
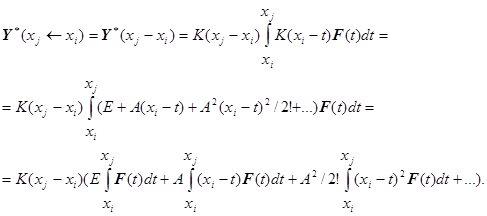
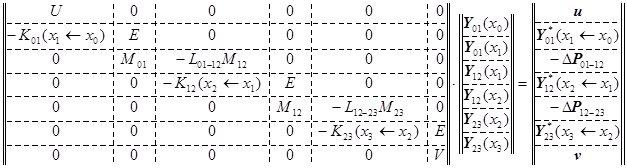
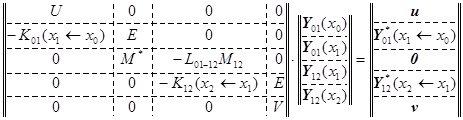
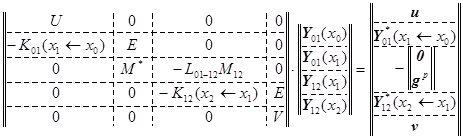


0 комментариев