Навигация
Формула для начала счета методом прогонки С.К.Годунова
7 Формула для начала счета методом прогонки С.К.Годунова
Эта формула обсчитана на компьютерах в кандидатской диссертации.
Рассмотрим проблему метода прогонки С.К.Годунова.
редположим, что рассматривается оболочка ракеты. Это тонкостенная труба. Тогда система линейных обыкновенных дифференциальных уравнений будет 8-го порядка, матрица A(x) коэффициентов будет иметь размерность 8х8, искомая вектор-функция Y(x) будет иметь размерность 8х1, а матрицы краевых условий будут прямоугольными горизонтальными размерности 4х8.
Тогда в методе прогонки С.К.Годунова для такой задачи решение ищется в следующем виде:
Y(x) = Y![]() (x) c
(x) c![]() + Y
+ Y![]() (x) c
(x) c![]() + Y
+ Y![]() (x) c
(x) c![]() + Y
+ Y![]() (x) c
(x) c![]() + Y*(x),
+ Y*(x),
или можно записать в матричном виде:
Y(x) = Y![]() (x) ∙ c + Y*(x),
(x) ∙ c + Y*(x),
где векторы Y![]() (x), Y
(x), Y![]() (x), Y
(x), Y![]() (x), Y
(x), Y![]() (x) – это линейно независимые вектора-решения однородной системы дифференциальных уравнений, а вектор Y*(x) – это вектор частного решения неоднородной системы дифференциальных уравнений.
(x) – это линейно независимые вектора-решения однородной системы дифференциальных уравнений, а вектор Y*(x) – это вектор частного решения неоднородной системы дифференциальных уравнений.
Здесь Y![]() (x)=|| Y
(x)=|| Y![]() (x), Y
(x), Y![]() (x), Y
(x), Y![]() (x), Y
(x), Y![]() (x) || это матрица размерности 8х4, а c это соответствующий вектор размерности 4х1из искомых констант c
(x) || это матрица размерности 8х4, а c это соответствующий вектор размерности 4х1из искомых констант c![]() ,c
,c![]() ,c
,c![]() ,c
,c![]() .
.
Но вообще то решение для такой краевой задачи с размерностью 8 (вне рамок метода прогонки С.К.Годунова) может состоять не из 4 линейно независимых векторов Y![]() (x), а полностью из всех 8 линейно независимых векторов-решений однородной системы дифференциальных уравнений:
(x), а полностью из всех 8 линейно независимых векторов-решений однородной системы дифференциальных уравнений:
Y(x)=Y![]() (x)c
(x)c![]() +Y
+Y![]() (x)c
(x)c![]() +Y
+Y![]() (x)c
(x)c![]() +Y
+Y![]() (x)c
(x)c![]() +
+
+Y![]() (x)c
(x)c![]() +Y
+Y![]() (x)c
(x)c![]() +Y
+Y![]() (x)c
(x)c![]() +Y
+Y![]() (x)c
(x)c![]() +Y*(x),
+Y*(x),
И как раз трудность и проблема метода прогонки С.К.Годунова и состоит в том, что решение ищется только с половиной возможных векторов и констант и проблема в том, что такое решение с половиной констант должно удовлетворять условиям на левом крае (стартовом для прогонки) при всех возможных значениях констант, чтобы потом найти эти константы из условий на правом крае.
То есть в методе прогонки С.К.Годунова есть проблема нахождения таких начальных значений Y![]() (0), Y
(0), Y![]() (0), Y
(0), Y![]() (0), Y
(0), Y![]() (0), Y*(0) векторов Y
(0), Y*(0) векторов Y![]() (x), Y
(x), Y![]() (x), Y
(x), Y![]() (x), Y
(x), Y![]() (x), Y*(x), чтобы можно было начать прогонку с левого края x=0, то есть чтобы удовлетворялись условия U∙Y(0) = u на левом крае при любых значениях констант c
(x), Y*(x), чтобы можно было начать прогонку с левого края x=0, то есть чтобы удовлетворялись условия U∙Y(0) = u на левом крае при любых значениях констант c![]() ,c
,c![]() ,c
,c![]() ,c
,c![]() .
.
Обычно эта трудность «преодолевается» тем, что дифференциальные уравнения записываются не через функционалы, а через физические параметры и рассматриваются самые простейшие условия на простейшие физические параметры, чтобы начальные значения Y![]() (0), Y
(0), Y![]() (0), Y
(0), Y![]() (0), Y
(0), Y![]() (0), Y*(0) можно было угадать. То есть задачи со сложными краевыми условиями так решать нельзя: например, задачи с упругими условиями на краях.
(0), Y*(0) можно было угадать. То есть задачи со сложными краевыми условиями так решать нельзя: например, задачи с упругими условиями на краях.
Ниже предлагается формула для начала вычислений методом прогонки С.К.Годунова.
Выполним построчное ортонормирование матричного уравнения краевых условий на левом крае:
U∙Y(0) = u,
где матрица U прямоугольная и горизонтальная размерности 4х8.
В результате получим эквивалентное уравнение краевых условий на левом крае, но уже с прямоугольной горизонтальной матрицей U![]() размерности 4х8, у которой будут 4 ортонормированные строки:
размерности 4х8, у которой будут 4 ортонормированные строки:
U![]() ∙Y(0) = u
∙Y(0) = u![]() ,
,
где в результате ортонормирования вектор u преобразован в вектор u![]() .
.
Как выполнять построчное ортонормирование систем линейных алгебраических уравнений можно посмотреть в [Березин, Жидков].
Дополним прямоугольную горизонтальную матрицу U![]() до квадратной невырожденной матрицы W:
до квадратной невырожденной матрицы W:
W = 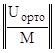 ,
,
где матрица М размерности 4х8 должна достраивать матрицу U![]() до невырожденной квадратной матрицы W размерности 8х8.
до невырожденной квадратной матрицы W размерности 8х8.
В качестве строк матрицы М можно взять те краевые условия, то есть выражения тех физических параметров, которые не входят в параметры левого края или линейно независимы с ними. Это вполне возможно, так как у краевых задач столько независимых физических параметров какова размерность задачи, то есть в данном случае их 8 штук и если 4 заданы на левом крае, то ещё 4 можно взять с правого края.
Завершим ортонормирование построенной матрицы W, то есть выполним построчное ортонормирование и получим матрицу W![]() размерности 8х8 с ортонормированными строками:
размерности 8х8 с ортонормированными строками:
W![]() =
= 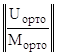 .
.
Можем записать, что
Y![]() (0) = (М
(0) = (М![]() )транспонированная = М
)транспонированная = М![]() .
.
Тогда, подставив в формулу метода прогонки С.К.Годунова, получим:
Y(0) = Y![]() (0) ∙с + Y*(0)
(0) ∙с + Y*(0)
или
Y(0) = М![]() ∙с + Y*(0).
∙с + Y*(0).
Подставим эту последнюю формулу в краевые условия U![]() ∙Y(0) = u
∙Y(0) = u![]() и получим:
и получим:
U![]() ∙ [ М
∙ [ М![]() ∙с + Y*(0) ]= u
∙с + Y*(0) ]= u![]() .
.
Отсюда получаем, что на левом крае константы c уже не на что не влияют, так как
U![]() ∙ М
∙ М![]() = 0 и остается только найти Y*(0) из выражения:
= 0 и остается только найти Y*(0) из выражения:
U![]() ∙ Y*(0) = u
∙ Y*(0) = u![]() .
.
Но матрица U![]() имеет размерность 4х8 и её надо дополнить до квадратной невырожденной, чтобы найти вектор Y*(0) из решения соответствующей системы линейных алгебраических уравнений:
имеет размерность 4х8 и её надо дополнить до квадратной невырожденной, чтобы найти вектор Y*(0) из решения соответствующей системы линейных алгебраических уравнений:
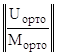 ∙ Y*(0) =
∙ Y*(0) = ![]() ,
,
где 0 – любой вектор, в том числе вектор из нулей.
Отсюда получаем при помощи обратной матрицы:
Y*(0) = 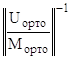 ∙
∙ ![]() ,
,
Тогда итоговая формула для начала вычислений методом прогонки С.К.Годунова имеет вид:
Y(0) = М![]() ∙с +
∙с + 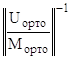 ∙
∙ ![]() .
.
Похожие работы
... матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются: , где матрицы Коши приближенно вычисляются по формуле: , где . 2. Метод решения жестких краевых задач без ортонормирования – метод сопряжения участков, выраженных матричными экспонентами. Разделим интервал интегрирования краевой задачи, например, на 3 участка. Будем иметь точки (узлы), ...
... . 4. Какие основные факторы нужно определить прежде, чем формировать инвестиционный портфель клиента? 5. Опишите простую структуру инвестиционного портфеля. ВВЕДЕНИЕ РАЗВИТИЕ РЫНКА ЦЕННЫХ БУМАГ В РОССИИ И ЗАДАЧИ РЕГУЛИРОВАНИЯ Рынок ценных бумаг в России начал свое формирование в первой половине 1991 г. после принятия известного Постановления Совета министров РСФСР ¹ 601 от 25 ...
... . А организованная преступность ещё имеет причины общие с неорганизованной преступностью. 3.3 Методы борьбы с организованной преступностью.21 В основе предупреждения организованной преступности лежат общесоциальные и экономические меры.Прежде всего нужны эффективные законы, отвечающие характеру современной преступности. Сегодняшний уголовный закон ...
... на поздних стадиях начинают проявляться ряд факторов объективного, природного характера, осложняющие ситуацию в решении парафиновой проблемы и снижающие эффективность традиционных мероприятий. 3.3 Методы используемые в НГДУ “Нурлатнефть” по предотвращению отложений АСПО 3.3.1 Механические методы борьбы с АСПО и технология работ при их применении Группа механических методов борьбы с ...
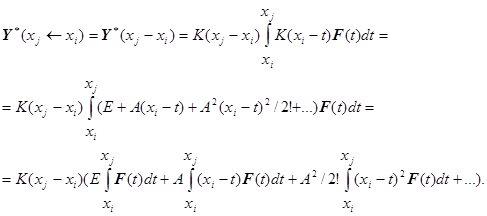
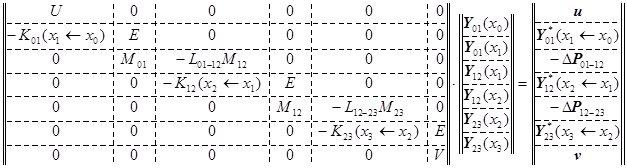
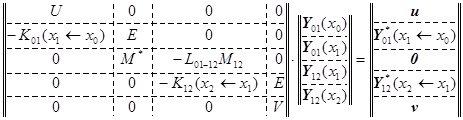
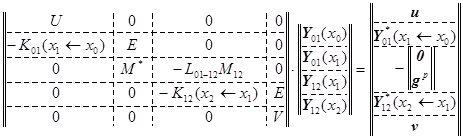


0 комментариев