Формула для вычисления вектора частного решения неоднородной системы дифференциальных уравнений
Метод «переноса краевых условий» в произвольную точку интервала интегрирования
Второй вариант метода «переноса краевых условий» в произвольную точку интервала интегрирования
Метод дополнительных краевых условий
Формула для начала счета методом прогонки С.К.Годунова
Второй алгоритм для начала счета методом прогонки С.К.Годунова
Применяемые формулы ортонормирования
Вывод формул, позаимствованный из «Теории матриц» Гантмахера
Навигация
Метод дополнительных краевых условий
Методы решения краевых задач, в том числе "жестких" краевых задач
32594
знака
0
таблиц
1
изображение
6 Метод дополнительных краевых условий
Этот метод еще не обсчитан на компьютерах.
Запишем на левом крае ещё одно уравнение краевых условий:
M ∙ Y(0) = m .
В качестве строк матрицы M можно взять те краевые условия, то есть выражения тех физических параметров, которые не входят в параметры краевых условий левого края L или линейно независимы с ними. Это вполне возможно, так как у краевых задач столько независимых физических параметров какова размерность задачи, а в параметры краевых условий входит только половина физических параметров задачи. То есть, например, если рассматривается задача об оболочке ракеты, то на левом крае могут быть заданы 4 перемещения. Тогда для матрицы М можно взять параметры сил и моментов, которых тоже 4, так как полная размерность такой задачи – 8. Вектор m правой части неизвестен и его надо найти и тогда можно считать, что краевая задача решена, то есть сведена к задаче Коши, то есть найден вектор Y(0) из выражения:
∙ Y(0) = 
,
то есть вектор Y(0) находится из решения системы линейных алгебраических уравнений с квадратной невырожденной матрицей коэффициентов, состоящей из блоков U и M.
Аналогично запишем на правом крае ещё одно уравнение краевых условий:
N ∙ Y(0) = n ,
где матрица N записывается из тех же соображений дополнительных линейно независимых параметров на правом крае, а вектор n неизвестен.
Для правого края тоже справедлива соответствующая система уравнений:
∙ Y(1) = 
.
Запишем Y(1) = K(1←0) ∙Y(0) + Y*(1←0) и подставим в последнюю систему линейных алгебраических уравнений:
∙ [ K(1←0) ∙Y(0) + Y*(1←0) ] = ,
∙ K(1←0) ∙Y(0) = - ∙ Y*(1←0),
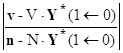∙ K(1←0) ∙Y(0) = 
,
∙ K(1←0) ∙Y(0) = 
.
Запишем вектор Y(0) через обратную матрицу:
Y(0) =
∙
и подставим в предыдущую формулу:
∙ K(1←0) ∙ ∙ = .
Таким образом, мы получили систему уравнений вида:
В ∙ = ,
где матрица В известна, векторы u и s известны, а векторы m и t неизвестны.
Разобьем матрицу В на естественные для нашего случая 4 блока и получим:
∙ = ,
откуда можем записать, что
В11 ∙ u + B12 ∙ m = s,
B21 ∙ u + B22 ∙ m = t.
Следовательно, искомый вектор m вычисляется по формуле:
m = B12
∙ (s – B11∙ u).
А искомый вектор n вычисляется через вектор t:
t = B21 ∙ u + B22 ∙ m,
n = t + N ∙ Y*(1←0).
В случае «жестких» дифференциальных уравнений предлагается выполнять поочередное построчное ортонормирование.
Запишем приведенную выше формулу
∙ K(1←0) ∙ ∙ =
в виде:
∙ K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) ∙ ∙ = .
Эту формулу можно записать в виде разделения левой части на произведение матрицы на вектор:
[ ∙ K(1←x2) ] ∙ { K(x2←x1) ∙ K(x1←0) ∙ ∙ } =
[ матрица ] ∙ { вектор } = вектор
Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[ ∙ K(1←x2) ]
{ K(x2←x1) ∙ K(x1←0) ∙ ∙ } = 
Здесь следует сказать, что подвектор t подвергать преобразованию не нужно, так как невозможно, так как его первоначальное значение не известно. Но подвектор t нам оказывается и не нужен для решения задачи.
Далее запишем:
[[ ∙ K(1←x2) ] ∙ K(x2←x1)] { K(x1←0) ∙ ∙ } =
[ матрица ] { вектор } = вектор
Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[[ ∙ K(1←x2) ]
K(x2←x1)] { K(x1←0) ∙ } = 
.
И так далее.
В результате поочередного ортонормирования получим:
В
∙ = ,
∙ = .
Следовательно, искомый вектор m вычисляется по формуле:
m = B12
∙ (s – B11∙ u).
Похожие работы
11612
0
6
... матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются: , где матрицы Коши приближенно вычисляются по формуле: , где . 2. Метод решения жестких краевых задач без ортонормирования – метод сопряжения участков, выраженных матричными экспонентами. Разделим интервал интегрирования краевой задачи, например, на 3 участка. Будем иметь точки (узлы), ...
... . 4. Какие основные факторы нужно определить прежде, чем формировать инвестиционный портфель клиента? 5. Опишите простую структуру инвестиционного портфеля. ВВЕДЕНИЕ РАЗВИТИЕ РЫНКА ЦЕННЫХ БУМАГ В РОССИИ И ЗАДАЧИ РЕГУЛИРОВАНИЯ Рынок ценных бумаг в России начал свое формирование в первой половине 1991 г. после принятия известного Постановления Совета министров РСФСР ¹ 601 от 25 ...
... . А организованная преступность ещё имеет причины общие с неорганизованной преступностью. 3.3 Методы борьбы с организованной преступностью.21 В основе предупреждения организованной преступности лежат общесоциальные и экономические меры.Прежде всего нужны эффективные законы, отвечающие характеру современной преступности. Сегодняшний уголовный закон ...
... на поздних стадиях начинают проявляться ряд факторов объективного, природного характера, осложняющие ситуацию в решении парафиновой проблемы и снижающие эффективность традиционных мероприятий. 3.3 Методы используемые в НГДУ “Нурлатнефть” по предотвращению отложений АСПО 3.3.1 Механические методы борьбы с АСПО и технология работ при их применении Группа механических методов борьбы с ...
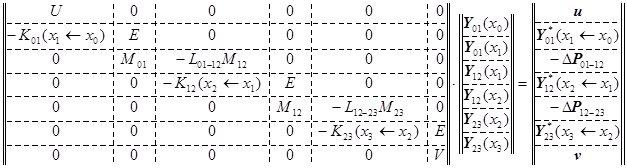
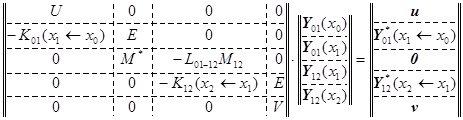
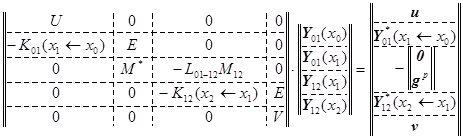
0 комментариев