Корисний сигнал з двома і більше гармоніками

4.5 Корисний сигнал з двома і більше гармоніками

Наступні експерименти були проведені з метою з’ясування можливостей алгоритму НК з використанням сімейств фільтрів AR(1) визначати кількість перетинів нульового рівня корисним сигналом, що складається з двох гармонік.

Для проведення цього експерименту було зроблено генерування корисного сигналу, що складається з двох гармонік. Для першого випадку з першої та другої гармоніки (рисунок 4.9) і для другого - з першої та третьої (рисунок 4.10).

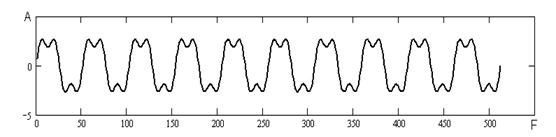
Рисунок 4.9 - Сигнал з двох гармонік для першого випадку.

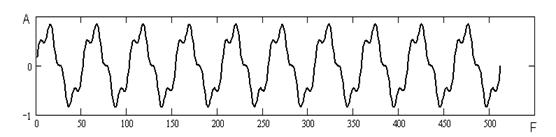
Рисунок 4.10 - Сигнал з двох гармонік для другого випадку.

При проведенні експериментів був використаний алгоритм HK з фільтру AR(1). Реалізація цього алгоритми була виконана з наступними параметрами:

- параметр , де k = 20 – кількість проходів по вхідної послідовності, N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність , D – число перетинів нуля на попередніх інтервалах;

- загальна довжина вхідної послідовності дорівнює 16384 точок;

- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;

- загальна довжина вхідної послідовності 16 секунд;

Експерименти були проведені, по схемі вже описаній у підрозділі 4.3.

Отримані результати було прийнято рішення подати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожний графік подає інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

На рисунку 4.11 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту  ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5.

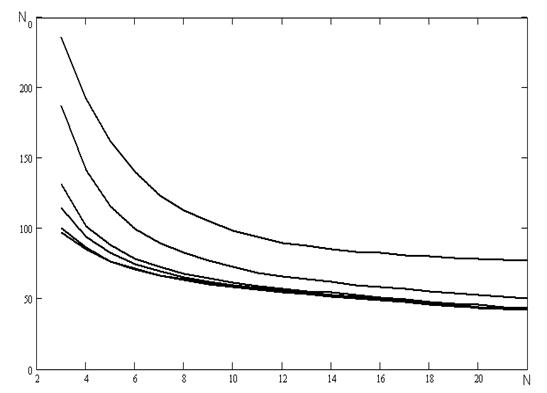
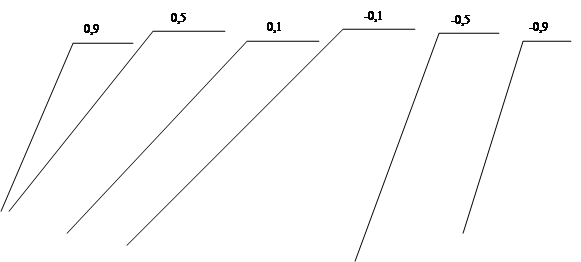Рисунок 4.11 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.6 та А.7.

На рисунку 4.12 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту  ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5

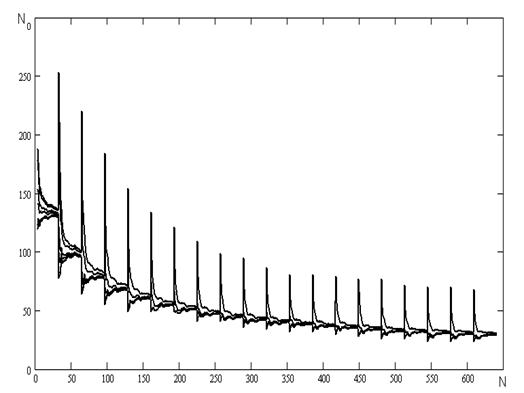
Рисунок 4.12 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.8 та А.9.

З наведених результатів експериментів можна зробити висновки стосовно того, що алгоритму НК з використанням сімейств фільтрів AR(1) можна використовувати для визначення кількості перетинів корисного сигналу, після його перекручування завадою.

Висновки:

- результати при використанні двох підтипів алгоритмів сходяться до різних значень через різні гармонічні складові вхідного корисного сигналу;

- завдяки де яким технічним доробкам, що були наведені у другому розділі, основна енергія корисного сигналу концентрується в першій гармоніці. Це дозволяє використовувати описаний алгоритм при обробці даних, що будуть надходити від вихрового потоковимірювача з дослідженими варіантами вхідного сигналу.

4.6 Корисний сигнал, що змінює частоту у часі

Наступні експерименти були проведені з метою з’ясування можливостей алгоритму НК з використанням сімейств фільтрів AR(1) визначати кількість перетинів нульового рівня корисним сигналом, який динамічно змінює власну частоту випадковим чином.

Для проведення цього експерименту було зроблено генерування синусоїди з випадковою зміною частоти. Після розбивання отриманого сигналу на тридцять два інтервали було з’ясовано, що на кожний інтервал у середньому припало приблизно 19.8 перетинів нульового рівня.

При проведенні експериментів був використаний алгоритм HK з фільтру AR(1). Реалізація цього алгоритми була виконана з наступними параметрами:

- параметр , де k = 20 – кількість проходів по вхідної послідовності, N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність , D – число перетинів нуля на попередніх інтервалах;

- загальна довжина вхідної послідовності дорівнює 16384 точок;

- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;

- загальна довжина вхідної послідовності 16 секунд;

Експерименти були проведені по схемі вже описаній у підрозділі 4.3.

Після отримання результатів для їх відображення було прийнято рішення подати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожний графік подає інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

На рисунку 4.13 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту  ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5

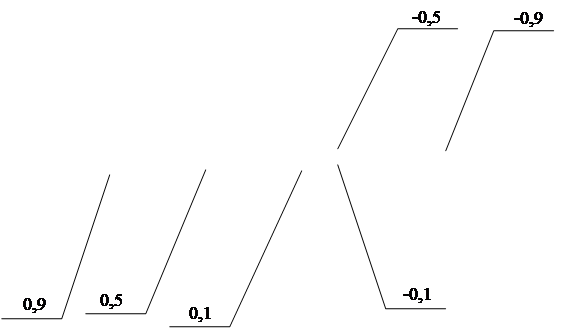
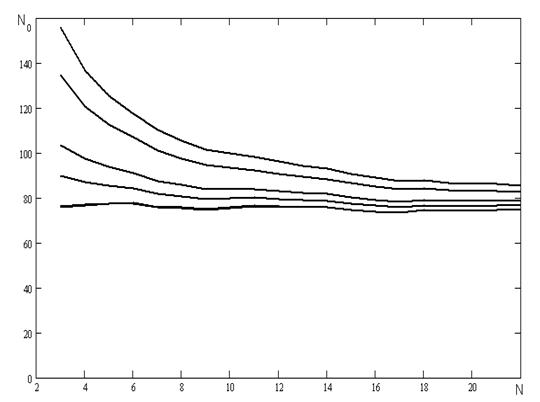
Рисунок 4.13 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.10 та А.11.

На рисунку 4.14 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту  ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 0,5

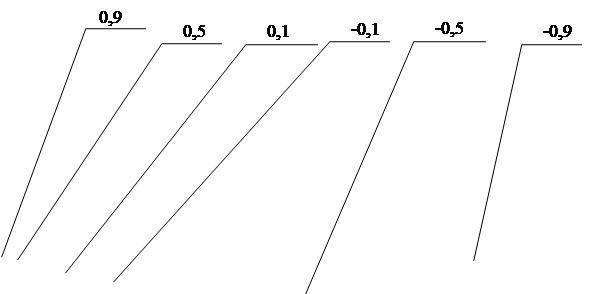
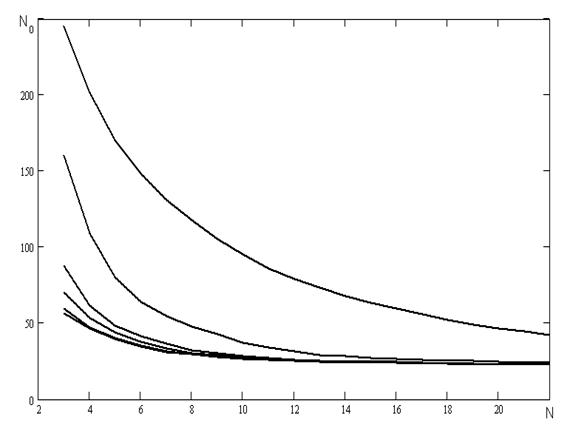
Рисунок 4.14 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Експерименти з іншими параметрами наведені в додатку А на рисунках А.12 та А.13.

З наведених результатів експериментів можна зробити висновки стосовно того, що, при використанні алгоритму НК з сімейств фільтрів AR(1), для виявлення кількості перетинів нульового рівня корисним сигналом, який динамічно змінює власну частоту випадковим чином.

Висновки такі:

- вихідні результати мають досить велику похибку.

- для того щоб обійти цю заваду потрібно буде розбивати вхідну послідовність на невеликі частини, щоб зміна частоти у ній була не дуже значною. За таких умов описаний алгоритм можна буде використовувати для обробки даних від вихрового потоковимірювача;

- також потрібно дослідити (попередньо реальні умови яких будуть проходити вимірювання швидкості потоків) на наявність швидких, різких та частих змін параметрів потоку. У реальних потоків дуже швидко параметри не змінюються, зазвичай, через згладжування різких коливань.