Навигация
НК – алгоритм. Параметричний фільтр АR(1)
4.3 НК – алгоритм. Параметричний фільтр АR(1)
Ітеративна схема, наведена нижче, ілюструє метод для виявлення однієї частоти у Гаусовому шумі. Наша модель це (4.1) з р = 1 та ![]() білим Гаусовим шумом. Алгоритм має собою наступні гарантії збіжності НОС послідовності до частоти
білим Гаусовим шумом. Алгоритм має собою наступні гарантії збіжності НОС послідовності до частоти ![]() у нашій моделі. Сімейство фільтрів це експоненціальний фільтр, що згладжує, або авторегрсійний порядку 1, АR(1)-фільтр.
у нашій моделі. Сімейство фільтрів це експоненціальний фільтр, що згладжує, або авторегрсійний порядку 1, АR(1)-фільтр.
Фільтр АR(1), відомий як (![]() - фільтр) визначається операцією:
- фільтр) визначається операцією:
![]() , (4.7)
, (4.7)
або еквівалентно в його рекурсивній формі:
![]() , (4.8)
, (4.8)
де квадрат коефіцієнта передачі фільтру ![]() заданий виразом:
заданий виразом:
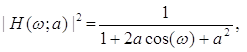
![]() (4.9)
(4.9)
де ![]()
Параметричний фільтр АR(1) має фундаментальні властивості відносно білого шуму [15].
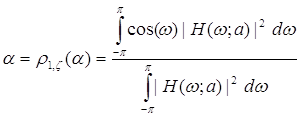 (4.10)
(4.10)
Тому НОС послідовність ![]() та
та ![]() на практиці емпіричні числа або ті, що спостерігаються, перетинів нуля обчислюються по формулі Е[Dak] на кожній стадії в ітерації і шумовий процес не обов’язково повинен бути білим – він повинен бути з неперервним спектром. На рисунку 4.1 можна побачити як підстроюється параметр
на практиці емпіричні числа або ті, що спостерігаються, перетинів нуля обчислюються по формулі Е[Dak] на кожній стадії в ітерації і шумовий процес не обов’язково повинен бути білим – він повинен бути з неперервним спектром. На рисунку 4.1 можна побачити як підстроюється параметр ![]() в залежності від вхідного сигналу у конкретному випадку при використанні даного алгоритму на практиці.
в залежності від вхідного сигналу у конкретному випадку при використанні даного алгоритму на практиці.
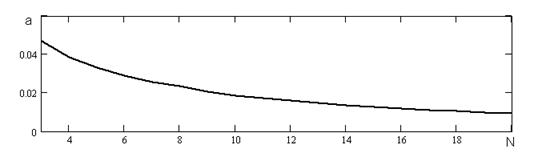
Рисунок 4.1 - Зміна параметра ![]() на протязі двадцяти ітерацій.
на протязі двадцяти ітерацій.
На рисунку 4.2 показано, як в процесі двадцяти ітерацій змінюється спектр сигналу. Можна побачити, як коефіцієнт передачі, рівномірний по всіх частотах, поступово переходить у бік низьких частот, тим самим виділяючи потрібну частоту корисного сигналу.
|
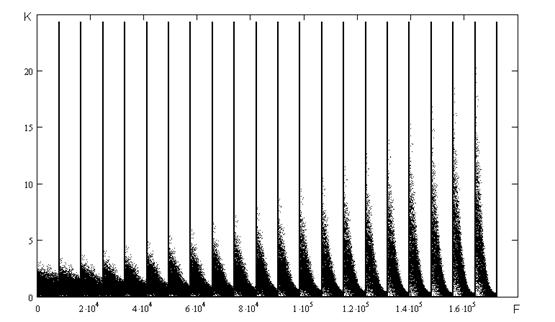
Рисунок 4.2 – Зміна спектру сигналу під час обробки алгоритмом НК.
К – енергетична складова гармонік, N – кількість перетинів нульового рівня
Далі буде показана реалізація алгоритму HK з використанням фільтру AR(1). Реалізація цього алгоритми була виконана з наступними параметрами:
- параметр ![]() , де k = 20 – кількість проходів по вхідної послідовності, N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність , D – число перетинів нуля на попередніх інтервалах;
, де k = 20 – кількість проходів по вхідної послідовності, N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність , D – число перетинів нуля на попередніх інтервалах;
- кількість точок на одному інтервалі Ni дорівнює 512;
- кількість періодів синусоїди в одному інтервалі дорівнює 10 і відповідно
кількість перетинів нульового рівня – 20;
- загальна довжина вхідної послідовності дорівнює 16384 точок;
- точок відліку на один період припадає 51;
- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;
- частота синусоїди дорівнює 20.0784 Гц;
- загальна довжина вхідної послідовності 16 секунд;
- кількість перетинів нуля вхідної послідовності 639.
Для проведення експерименту по виявленню корисного сигналу на фоні завади, була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Перед використанням алгоритму HK з фільтру AR(1) попередньо синусоїду з відомими параметрами змішуємо з отриманим шумом. Далі, під час проведення експерименту, можна простежити, як цей алгоритм знаходить у зашумованому сигналі потрібну частоту. Цей процес на протязі двадцяти ітерацій, з новим обчисленням параметру ![]() після проходження усієї вхідної послідовності, можна спостерігати на рисунку 4.3.
після проходження усієї вхідної послідовності, можна спостерігати на рисунку 4.3.
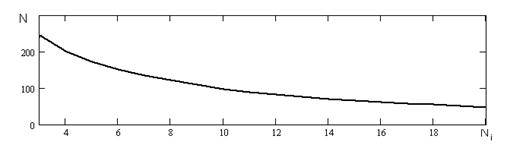
Рисунок 4.3 - Пошук потрібної кількості перетинів нульового рівня вхідним сигналом. Nі - номер ітерації алгоритму, N – кількість перетинів нульового рівня.
Зміну поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру ![]() після кожного інтервалу вхідної послідовності, можна спостерігати на рисунку 4.4.
після кожного інтервалу вхідної послідовності, можна спостерігати на рисунку 4.4.
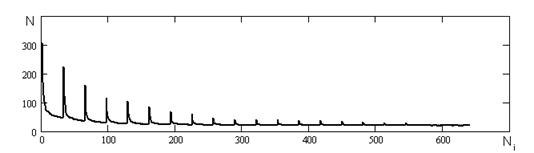
Рисунок 4.4 - Пошук потрібної кількості перетинів нульового рівня вхідним сигналом.
На рисунку 4.4 спостерігаються підвищення поточної кількості перетинів нульового рівня вхідним сигналом рівномірно через однакові проміжки часу. Це пов’язано з тим, що алгоритм починає проходження вхідної послідовності з початку, а історія обчислень була накопичена на інтервалах в кінці послідовності і послідовність була змінена. Тому відбувається швидке підстроювання параметрів під нові інтервали.
З метою визначення ефективності даного алгоритму при обробці сигналу, в якому ефективно значення шуму відносно сигналу дорівнює, більше та менше. Для зручності співвідношення сигнал/завада обираємо наступними: 2, 1, 0,5. Також паралельно провадилися експерименти з ініціалізацією початкового значення параметру ![]() наступними значеннями 0,1, 0,5, 0,9, -0,1, -0,5, -0,9.
наступними значеннями 0,1, 0,5, 0,9, -0,1, -0,5, -0,9.
За для зручності аналізу отриманих результатів було прийнято рішення подавати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожен графік буде подавати інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру ![]() .
.
Описані експерименти проводилися для двох різновидів алгоритмів HK з використанням фільтру сімейства AR(1).
У першому варіанті алгоритму проводилася зміна поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру ![]() після кожного інтервалу вхідної послідовності.
після кожного інтервалу вхідної послідовності.
У другому варіанті алгоритму проводилася зміна поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру ![]() після проходження усієї вхідної послідовності.
після проходження усієї вхідної послідовності.
Для отримання моделі завади була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Її амплітуда при генерації задавалася за допомогою стандартного математичного відхилення. Для порівняння амплітуди синусоїди з завадою використовувалося діюче значення амплітуди сигналу синусоїди.
На рисунку 4.5 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- не в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 0,5.

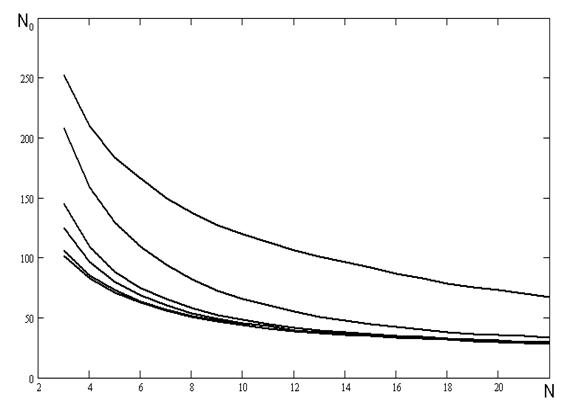
Рисунок 4.5 - Залежність кількості перетинів нульового рівня від частоти. Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
Експерименти з іншими параметрами наведені в додатку А на рисунках А.1 та А.2.
На рисунку 4.6 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 0.5.
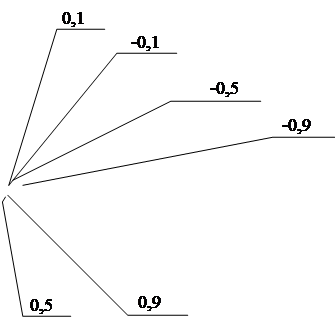
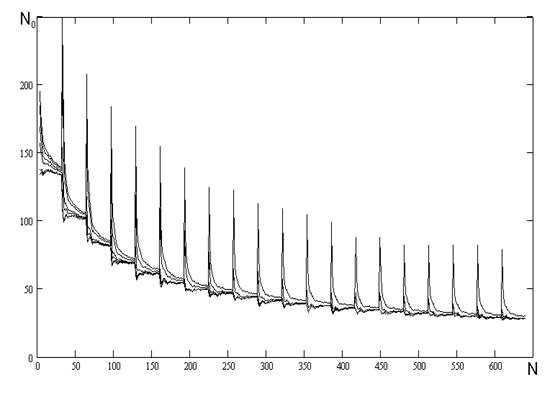
Рисунок 4.6 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку 4.7 наведене у збільшеному масштабі результати попереднього експерименту. Це було зроблено для того, щоб більш детально розглянути момент в роботі алгоритму HK з використанням фільтру сімейства AR(1), коли проводиться зміна поточного кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру ![]() після кожного інтервалу вхідної послідовності. Це потрібно для щоб детально показати які стрибки відбуваються під час переходу обробки вхідного сигналу з кінця на початок і як їх амплітуда залежить від обирання початкового значення параметру
після кожного інтервалу вхідної послідовності. Це потрібно для щоб детально показати які стрибки відбуваються під час переходу обробки вхідного сигналу з кінця на початок і як їх амплітуда залежить від обирання початкового значення параметру ![]() .
.
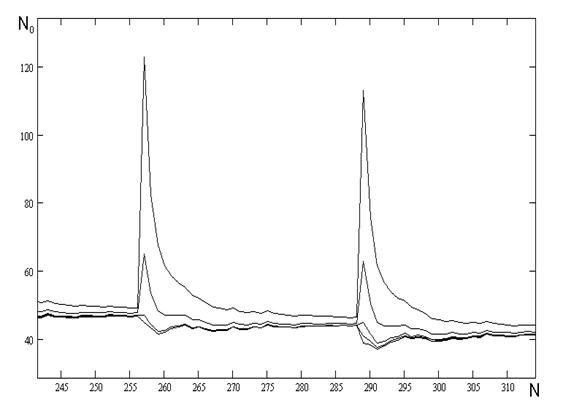
 Рисунок 4.7 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок 4.7 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
Експерименти з іншими параметрами наведені в додатку А на рисунках А.3 та А.4.
З проведених експериментів можна зробити висновки стосовно обирання початкового значення параметру ![]() для отримання потрібної частоти за найменшу кількість ітерацій, ефективності двох типів алгоритмів HK з використанням фільтру сімейства AR(1), швидкості знаходження потрібної частоти в залежності від співвідношення сигнал/шум.
для отримання потрібної частоти за найменшу кількість ітерацій, ефективності двох типів алгоритмів HK з використанням фільтру сімейства AR(1), швидкості знаходження потрібної частоти в залежності від співвідношення сигнал/шум.
Висновки такі:
- як і очікувалося, при збільшенні співвідношення сигнал/шум швидкість сходження алгоритму до конкретного значення збільшується;
- найкращі результати були отримані при використанні початкового значення ![]() = 0.9;
= 0.9;
- результати використання обох алгоритмів НК приблизно однакові.
0 комментариев