Обчислювальні експерименти без урахування квадратичної залежності амплітуди від частоти

3.1 Обчислювальні експерименти без урахування квадратичної залежності амплітуди від частоти

3.1.1 Фільтрація ковзкого згладжування

Генератором випадкового шуму був обраний стандартний генератор псевдовипадкових чисел c нормальним розподілом у MathCad2001 і генератор псевдовипадкових чисел на зсувних регістрах c зворотним зв'язком, що використовує поліном [10]:

, (3.1)

де - значення самого поліному;

ⁿ – значення відповідних розрядів, де n – номер розряду у вхідному числі.

Були визначені характеристики отриманих псевдовипадкових послідовностей.

До цього шуму був доданий корисний сигнал, що являє собою синусоїду. Формула (1) призначена для обмеженої смуги частот, тому отриману нами суміш шуму й корисного сигналу потрібно пропустити через фільтр.

Для фільтрації обраний метод ковзного згладжування з двома проходами. У першому проході вибірку здійснювали по n=8 елементи, а в другому по n =6.

Потім для отриманої суміші шуму й корисного сигналу в процесі експерименту був проведений підрахунок кількості переходів через нульовий рівень (зі співвідношенням сигнал/шум, що дорівнює: 0.1, 0.5, 1, 5).

На рисунку 3.1 показані залежності, отримані з використанням стандартного генератора псевдовипадкових чисел і на рисунку 3.2 - з використанням генератора псевдовипадкових чисел на ЗРЗЗ.

З використанням формули 3.1 були отримані залежності кількості переходів через нульовий рівень від частоти (при таких же співвідношеннях сигнал/шум). Цей графік подано на рисунку 3.3.

Експеримент з використанням стандартного генератору псевдовипадкових чисел c нормальним розподілом у MathCad2001 був проведений з наступними параметрами:

максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда шуму (середньоквадратичне відхилення) обиралася в залежності від відношення сигнал-шум та діючого значення амплітуди шуму;

Експеримент з використанням генератора псевдовипадкових чисел на ЗРЗЗ був проведений з наступними параметрами:

- максимальна амплітуда шуму 2048

- амплітуда синусоїди 1.5 В (ефективне значення);

- амплітуда синусоїди (ефективне значення) обиралася в залежності від відношення сигнал-шум та середньоквадратичного відхилення шуму.

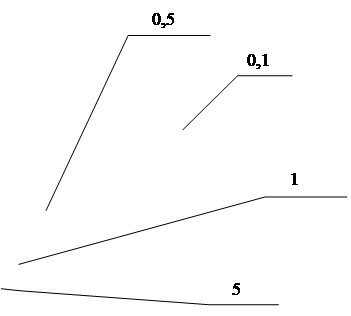Рисунок 3.1 - Залежність кількості перетинань нульового рівня від частоти отримані з використанням стандартного генератора псевдовипадкових чисел.

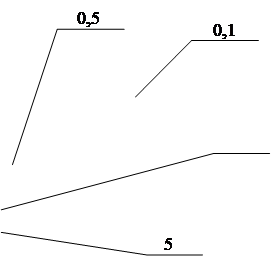
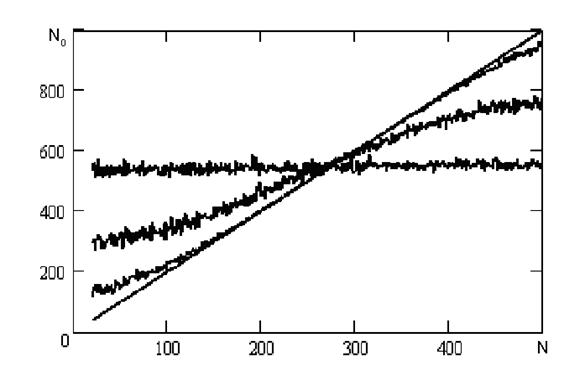
Рисунок 3.2 - Залежність кількості перетинань нульового рівня від частоти отримані з використанням генератора псевдовипадкових чисел на ЗРЗЗ.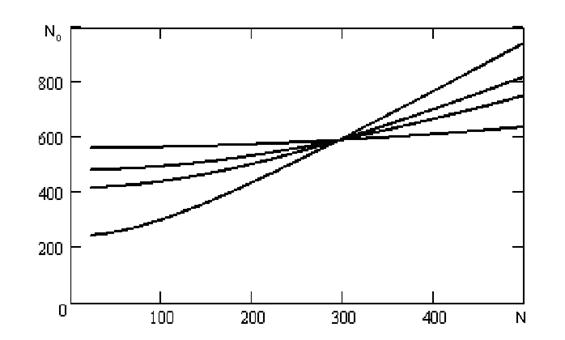

Рис. 3.3 - Залежність кількості перетинань нульового рівня від частоти, отримана з використанням формули 3.1.

Як видно з отриманих результатів, характеристики, отримані аналітично й експериментально, мають спільні риси. Причому, є точка перетинання всіх кривих. Однак, у формулі 3.1 не враховується квадратична залежність амплітуди сигналу від частоти. Обчислюється математичне очікування кількості нулів не за певну кількість періодів, а за одиницю часу для суми синусоїдального сигналу й білого шуму з обмеженою смугою частот.

3.1.2 Аперіодичний фільтр

На практиці складно реалізувати фільтр ковзного згладжування, а RC-фільтр набагато простіше. Тому проводимо ще один експеримент де фільтрацію зробимо за допомогою RC-фільтра. Гранична частота при фільтрації 500 Гц.

Експеримент з використанням стандартного генератору псевдовипадкових чисел c нормальним розподілом у MathCad2001 був проведений з наступними параметрами:

- максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда шуму (середньоквадратичне відхилення) обиралася в залежності від відношення сигнал-шум та діючого значення амплітуди шуму;

-  фільтра для частоти 500 Гц дорівнює 3,183 *10^-4;

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

Експеримент з використанням генератора псевдовипадкових чисел на СРОС був проведений з наступними параметрами:

- максимальна амплітуда шуму 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда синусоїди (ефективне значення) обиралася в залежності від відношення сигнал-шум та середньоквадратичного відхилення шуму;

-  фільтра для частоти 500 Гц дорівнює 3,183 *10^-4;

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

Результати експерименту з використанням генератора псевдовипадкових чисел на СРОС можна побачити на рисунку 3.4.

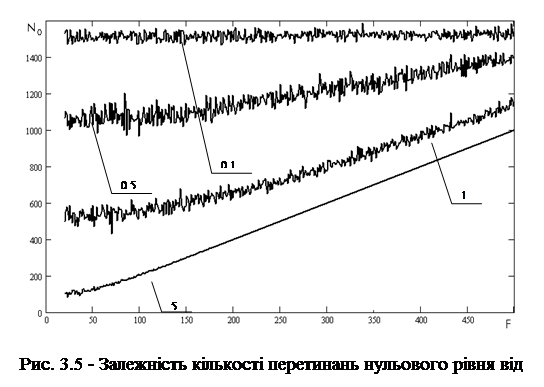
Результати експерименту з використанням стандартного генератору псевдовипадкових чисел у MathCad2001 можна побачити на рисунку 3.5. Помітні розбіжності спостерігаються при співвідношенні 0,1.