Комбінування алгоритму НК з попередньою фільтрацією фільтром низьких частот

5 Комбінування алгоритму НК з попередньою фільтрацією фільтром низьких частот

У подальших дослідженнях було прийнято рішення поєднати два методи для отримання кращих результатів. Спочатку проводиться фільтрація вхідної послідовності за допомогою фільтра нижніх частот, а потім проводиться обробка отриманої послідовності за допомогою алгоритму AR(1) для виявлення частоти корисного сигналу більш точним методом, ніж простим підрахунком перетинів корисного сигналу з нульовим рівнем.

Довжина вхідної послідовності зменшувалася пропорцій зменшенню частоти сигналу для того, щоб кількість перетинів нульового рівня залишалася постійною і дорівнювала 32 перетинам.

У сигналі від реального датчика присутній квадратична залежність амплітуди сигналу від частоти. Обчислюється математичне очікування кількості нулів за одиницю часу для суми синусоїдального сигналу й білого шуму з обмеженою смугою частот. У подальших експериментах використовується квадратична залежність між частотою та ефективним значенням амплітуди корисного сигналу

В процесі проведення цього експерименту синусоїда генерувалася кожного разу заново для нової частоти на всьому діапазоні частот, що досліджуються. Для отримання моделі перешкоди була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Її амплітуда при генерації задавалася за допомогою математичного відхилення. Для порівняння амплітуди синусоїди з перешкодою використовувалося діюче значення амплітуди сигналу синусоїди. Амплітуда синусоїди обиралася в залежності співвідношення сигнал/шум на початку експерименту.

При проведенні експериментів був використаний алгоритм HK з фільтру AR(1). Реалізація цього алгоритми була виконана з наступними параметрами:

- , де k = 20 – кількість проходів по вхідної послідовності, N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність, D – число перетинів нуля на попередніх інтервалах;

- мінімальна кількість точок дискретизації на період синусоїди 10;

- мінімальна частота корисного сигналу 20 Гц;

- максимальна частота корисного сигналу 500 Гц;

- довжина випадкової реалізації 4096;

- максимальна амплітуда синусоїди 2048

- амплітуда синусоїди 1.5 В (ефективне значення амплітуди);

- амплітуда шуму (середньоквадратичне відхилення) обиралася в залежності від відношення сигнал-шум та діючого значення амплітуди шуму;

- дискретизація фільтру дорівнює 8 по 0,0002 с, що забезпечує помилку меншу за 1 %.

За для зручності аналізу отриманих результатів було прийнято рішення подавати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожний графік подає інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

З метою визначення ефективності даного алгоритму при обробці сигналу, в якому перешкода відносно сигналу дорівнює, більше та менше. Для зручності співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

Початкове значення коефіцієнту  ініціалізується значеннями: 0,5;

Обробка еквівалентна проходженню через інтегруючий RC-фільтр.

На рисунку 5.1 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту  ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму на ЗРЗЗ;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

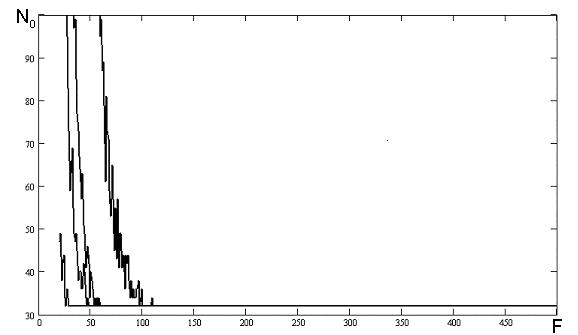
Рисунок 5.1 - Залежність числа перетинів нульового рівня від частоти. Використаний генератор псевдовипадкових чисел на ЗРЗЗ.

Обробка еквівалентна проходженню через інтегруючий RC-фільтр.

На рисунку 5.2 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту  ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму стандартний з середовища Mathcad;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

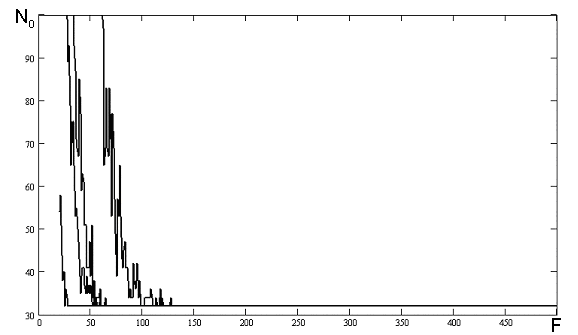
Рисунок 5.2 - Залежність числа перетинів нульового рівня від частоти. Використаний генератор псевдовипадкових чисел стандартний з середовища Mathcad.

Обробка еквівалентна проходженню через інтегруючий RC-фільтр та подальшій обробці за допомогою AR(1) алгоритму.

На рисунку 5.3 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту  ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму на ЗРЗЗ;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

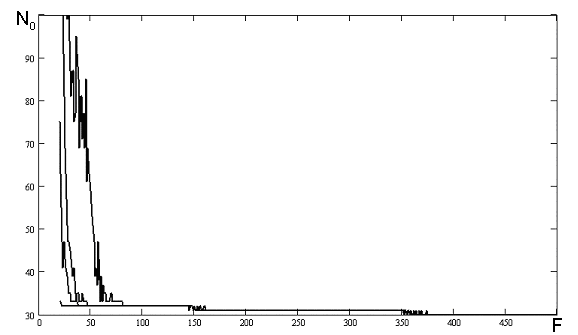
Рисунок 5.3 - Залежність числа перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел на ЗРЗЗ.

Додаткова обробка за допомогою НК алгоритму.

На рисунку 5.4 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- фільтр попередньої обробки – аперіодичний;

- початкове значення коефіцієнту  ініціалізується значеннями: 0,5;

- генератор псевдовипадкових чисел для моделі шуму стандартний з середовища Mathcad;

- співвідношення сигнал/перешкода обираємо наступними: 0.1, 0.5, 1, 5.

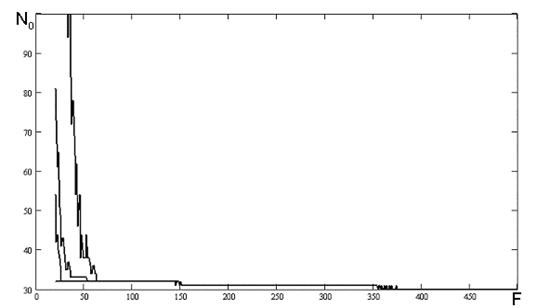
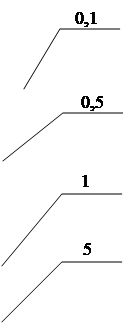Рисунок 5.4 - Залежність числа перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел стандартний з середовища Mathcad.

Додаткова обробка за допомогою НК алгоритму.

Висновки такі:

- на високих частотах на корисний сигнал від датчика завада майже не впливає, але на низьких, коли амплітуда корисного сигналу значно зменшується, через заваду дуже стрімко починаються з’являтися зайві перетини нульового рівня;

- після поєднання двох методів, які окремо покращували результати обробки, результати експериментів покращились;

- отримані результати суттєво розширили у бік низьких частот можливий діапазон вимірювань потоків при вимірювані за допомогою вихрового потоковимірювача.