Навигация
Відрахування на соціальні заходи
7.4.4 Відрахування на соціальні заходи
До елемента "Відрахування на соціальні заходи" ставляться:
а) відрахування на державне (обов'язкове) пенсійне страхування (у Пенсійний фонд) – 32 % від (![]() ):
):
![]() = 0,32·(
= 0,32·(![]() ), (7.11)
), (7.11)
![]() =0,32·(1672,00+167,20) =588,54 грн.;
=0,32·(1672,00+167,20) =588,54 грн.;
б) відрахування на державне (обов'язкове) соціальне страхування, включаючи відрахування на обов'язкове медичне страхування – 2,5 % від (![]() ):
):
![]() = 0,025·(
= 0,025·(![]() ), (7.12)
), (7.12)
![]() =0,025·(1672,00+167,20) =45,98 грн.;
=0,025·(1672,00+167,20) =45,98 грн.;
в) відрахування у Фонд сприяння зайнятості населення 2,5 % від (![]() ):
):
![]() =0,025·(
=0,025·(![]() ), (7.13)
), (7.13)
![]() =0,025·(1672,00+167,20) =45,98 грн.;
=0,025·(1672,00+167,20) =45,98 грн.;
г) страхування по травматизму 0,85% від (![]() ):
):
![]() =0,0085·(
=0,0085·(![]() ), (7.14)
), (7.14)
![]() =0,0085·(1672,00+167,20) =15,63 грн.
=0,0085·(1672,00+167,20) =15,63 грн.
7.4.5 Експлуатаційні витрати
При розробці даної науково-дослідної роботи для обробки результатів виміру й оформлення пояснювальної записки використався персональний комп'ютер. Розрахуємо витрати на машинний час:
Зекс=![]() ·nдн·
·nдн·![]() ·T, (7.15)
·T, (7.15)
де ![]() - кількість місяців, потрібна для розробки НДР (
- кількість місяців, потрібна для розробки НДР (![]() =5 міс.);
=5 міс.);
![]() - кількість робочих днів у місяці (
- кількість робочих днів у місяці (![]() =22 дня);
=22 дня);
![]() - кількість робочих годин за день на ЕОМ (
- кількість робочих годин за день на ЕОМ (![]() =2 год.);
=2 год.);
Т – тариф за використання ЕОМ, за годину (Т=2 грн.).
Зекс=5.·22·2.·2=440,00 грн.
7.4.6 Накладні витрати
Накладні витрати у відмінності від прямих витрат пов'язані із забезпеченням загальних умов при розробці науково-дослідної роботи з урахуванням амортизаційних відрахувань. При складанні кошторисів накладні витрати визначаються непрямим шляхом - установленою нормою стосовно витрат або стосовно основної заробітної плати. Накладні витрати становлять 30 % від ЗОСН:
ЗНВ=0,3·ЗОСН; (7.16)
ЗНВ=0,3·1672,00=501,60 грн.
7.4.7 Калькуляція собівартості
За результатами проведених розрахунків становимо калькуляцію собівартості, що представлена в таблиці 7.8.
Проведені розрахунки показують, що ціна продажу, рівна 4913,64 грн., прийнятна для представників малого й середнього бізнесу, а також і для державних підприємств, а вартість розробки склала 3639,73 грн., що говорить про те, що проведену роботу можна вважати економічно ефективної, що має високий науковий і економічний рівень.
Таблиця 7.8 - Калькуляція собівартості науково-дослідної роботи
| Найменування статей калькуляції | Сума, грн |
| 1 Матеріали | 162,80 |
| 2 Основна заробітна плата | 1672,00 |
| 3 Додаткова заробітна плата | 167,20 |
| 4 Відрахування на соціальні заходи А) пенсійне страхування Б) соціальне страхування В) зайнятість населення Г) травматизм | 588,54 45,98 45,98 15,63 |
| 5 Експлуатаційні витрати | 440,00 |
| 6 Накладні витрати | 501,60 |
| 7 Собівартість | 3639,73 |
| 8 Прибуток 35 % | 1273,91 |
| 9 Ціна продажу | 4913,64 |
7.5 Економічна ефективність НДР
Специфічною особливістю проведення ефективності НДР є їхній прогнозний характер, а також наявність невизначеності в області застосування й обсягах використання результатів НДР, у рівні витрат на виробництво, в оцінці впливу характеристик приладів на характеристики більше складних систем.
Визначення економічної ефективності НДР базується на загальних методах розрахунку порівняльної економічної ефективності нової техніки.
Кількісне визначення економічної ефективності НДР можливо, якщо є база для порівняння, відомі область і обсяг промислового використання результатів НДР. Однак, специфіка розрахунку економічної ефективності НДР полягає в тім, що результати НДР самостійного значення не мають, а дають економічний ефект у народному господарстві тільки будучи опосередкованими через довгий ланцюжок стадій технічного прогресу. Тому економічна ефективність НДР оцінюється по участі у відсотках від економічної ефективності нової техніки в цілому відповідно до ГОСТ 20779-81 [12] по формулі:
![]() , (7.17)
, (7.17)
де ![]() - частина річного ефекту, що доводиться на і-ту організацію або етап;
- частина річного ефекту, що доводиться на і-ту організацію або етап;
Э - загальний річний економічний ефект від створення й впровадження нової техніки або нового методу робіт;
![]() - коефіцієнт участі у відсотках і-ої організації або і-го етапу робіт:
- коефіцієнт участі у відсотках і-ої організації або і-го етапу робіт:
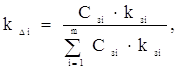 (7.18)
(7.18)
де ![]() - витрати на заробітну плату і-ої організації або і-го етапу робіт;
- витрати на заробітну плату і-ої організації або і-го етапу робіт;
![]() - коефіцієнт значимості і-го етапу;
- коефіцієнт значимості і-го етапу;
m - число організацій або етапів.
Економічну ефективність деяких пошукових і прикладних НДР розрахувати не вдається. У такому випадку приводять якісний опис соціально-економічної ефективності НДР за методикою, сутність якої полягає в тому, що на основі оцінок роботи визначається коефіцієнт науково-дослідного ефекту НДВКР [12]:
![]() , (7.19)
, (7.19)
де ![]() - ваговий коефіцієнт і-ої ознаки науково-технічного ефекту (таблиця 7.9);
- ваговий коефіцієнт і-ої ознаки науково-технічного ефекту (таблиця 7.9);
![]() - кількісна оцінка і-ої ознаки науково-технічного ефекту НДР.
- кількісна оцінка і-ої ознаки науково-технічного ефекту НДР.
Кількісна оцінка рівня новизни визначається по таблиці 7.10; теоретичний рівень отриманих результатів - на основі експертних оцінок з обліком даних таблиці 7.11; можливість реалізації наукових результатів - на основі суми значень балів таблиці 7.12 і таблиці 7.13
Таблиця 7.9 - Коефіцієнт вагомості ознак
| Ознака науково-технічного ефекту НДОКР | Значення вагового коефіцієнта |
| 1 Рівень новизни | 0,6 |
| 2 Теоретичний рівень | 0,4 |
| 3 Можливість реалізації | 0,2 |
Таблиця 7.10 - Ознака наукової новизни
| Рівень новизни розробки | Характеристика новизни | Бали |
| Абсолютно нова | Робота носить інноваційний характер в Україні. Вимірювання швидкості потоків в агресивних. | 8-10 |
Таблиця 7.11 - Ознака теоретичного рівня
| Теоретичний рівень отриманих результатів | Бали |
| Розробка способу (алгоритм, програма заходів, пристрій і т.д.) | 7-9 |
Таблиця 7.12 - Ознака часу реалізації
| Час реалізації | Бали |
| Перші чотири роки | 10 |
Таблиця 7.13 - Масштаби реалізації
| Масштаби реалізації | Бали |
| Народне господарство | 10 |
![]() балів,
балів,
де 0,6 - рівень новизни нашого виробу;
8 - нова розробка;
0,4 - теоретичний рівень;
7 - розробка способу;
0,2 - можливість реалізації;
20 = 10+2,
де 10 - можливість реалізації протягом перших чотирьох років;
2 - народним господарством.
На кожній розробці встановлюється ступінь наближення у відсотках отриманих значень науково-технічного ефекту до максимально можливого:
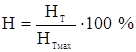 , (6.20)
, (6.20)
де ![]() балів – максимальне значення узагальнюючого показника науково-технічного ефекту.
балів – максимальне значення узагальнюючого показника науково-технічного ефекту.
![]() %.
%.
З наведеного вище розрахунку економічної ефективності видно, що новий виріб доцільно розробляти.
Основні техніко-економічні показники наведені в таблиці 7.14
Таблиця 7.14 - Техніко-економічні показники
| Найменування показника | Одиниці виміру | Значення |
| 2 Кошторисна вартість | грн. | 4913,64 |
| 3 Прибуток | грн. | 1273,91 |
| 4 Строк розробки | дн. | 83 |
| 5 Економічний ефект | % | 96,6 |
Результат розрахунку коефіцієнта науково-технічного ефекту (НТ=96,6 %) показує доцільність проведення даної роботи, а також подальших досліджень у цій області.
Висновки
В дипломній роботі було розглянуто декілька моделей фільтрів та зроблена їх оцінка стосовно їх можливого використання у розробці вихрового потоковимірювача. Розглянуті результати фільтрації непогано узгоджуються з аналітичними розрахунками Бендат Дж. [5]. Використання фільтрів розширює діапазон вимірювання за допомогою вихрового потоковимірювача. В процесі моделювання були використані два різних генератора псевдовипадкових чисел та була зроблена оцінка параметрів отриманих псевдовипадкових послідовностей. Були реалізований алгоритм НК з використанням сімейств фільтрів AR(1) та MА(1) що використовує параметричну фільтрацію для рекурсивного визначення частот дискретних спектральних компонент. Ці алгоритми мають покращити характеристики вихрового потоковимірювача. Для покрашення результатів обробки було досліджено вплив проведеної попередньо фільтрації з пригніченням високочастотних завад використанням алгоритму НК з використанням фільтру сімейства AR(1). Отримані результати дають змогу суттєво розширити у бік низьких частот можливий діапазон вимірювань потоків при вимірювані за допомогою вихрового потоковимірювача.
Список джерел інформації
1. Киясбейли А.Ш., Перельштейн М. Е. Вихревые измерительные приборы. Б-ка приборостроителя. М., «Машиностроение», 1978, 152 с.
2. Белоцерковский С. М. Турбулентность и вихревая аэродинамика.
3. Бакай А.С., Сигов Ю.С. Многоликая турбулентность,-М.: Знание,1989. С.3-12
4. Rice S. Mathematical analysis of random noise // Bell Syst. Tech. J., Vol.24, 1945.-P.46-156.
5. Бендат Дж. Основы теории случайных шумов и ее применения,-М.: Наука, 1965. С.429-431
6. Gajic B., Paliwal K. Robust speech recognition using features based on zero crossings with peak amplitudes // IEEE Intern. Conf. on Acoustics, Speech and Signal Processing, Vol.1, 2003.-P. 64-67.
7. Kedem B. Spectral Analysis and Discrimination by Zero-Crossings // IEEE, Vol. 74, 1986.-P.1475-1493.
8. He S., Kedem B. Higher Order crossings Spectral Analysis of an Almost Periodic Random Sequence in Noise // IEEE, Vol.35, 1989.-P.360-370.
9. Barnett, J., Kedem B. Zero-crossing rates of mixtures and products of Gaussian processes // IEEE, Vol.44, 1998.-P.1672-1677.
10. Питерсон У. Коды, исправляющие ошибки.-М.: МИР,1964.-С.288-307.
11. Troendle, J.F., An Iterative Filtering Method of Frequency Detection in a Mixed Spectrum Model. Doctoral Dissertation, Department of Mathematics, University of Maryland, College Park, 1991.
12. Matausek, M.R., S.S. Stankovic, and D.V. Radovic, "Iterative inverse filtering approach to the estimation of frequencies of noisy sinusoids," IEEE Tr. on Acoust. Speech Sig. Proc., ASSP-31, No. 6, pp. 1456-1463, 1983.
13. Li, T. and B. Kedem, "Improving Prony's estimator for multiple frequency estimation by a general method of parametric filtering," ICASSP-93, vol. IV, pp. 256-259, April 1993.
14. Dragosevic, M.V. and S.S. Stankovic, "A generalized least squares method for frequency estimation," IEEE Trans. Acoust., Speech, Signal Process., 37, No. 6, pp. 805-819, 1989.
15. J.T.Barnett., Zero-Crossing Rates of Some Non-Gaussian Processes with Application to Detection and Estimation, 1996.
16. Yakowitz, S., "Some contributions to a frequency location method due to He and Kedem," IEEE Trans. Infor. Theory, 37, No. 4, pp. 1177-1182, 1991.
17. Федоров А.А. Курс лекций по дисциплине: “Экономика и организация производства”.
18. Федоров А.А., Ланько А.В., Статейко Т.Г. Методические указания по технико-экономическому обоснованию дипломных работ (конструкторская часть)
АП-факультет.
19. Котлер Д.Н. Маркетинг, 2000г.
20. Омаров К.С. Организация производства.
21. ПУЭ-87. Правила устройства электроустановок.
- М.:Энергоатомиздат, 1987. - 648 с.
22. ГОСТ 12.1.005-88.ССБТ. Общие санитарно-гигиенические требования к воздуху рабочей зоны. - Введ. 01.01.89.
23. СНиП 2.04.05-86.Строительные нормы и правила. Отопление. Вентиляция и кондиционирование воздуха.-М.:Стройиздат, 1987-110с.
24. СНиП II-4-79. Строительные нормы и правила. Естественное и искусственное освещение. - М.: Стройиздат, 1980. - 48с.
25. ГОСТ 12.1.003-83.ССБТ. Шум. Общие требования безопасности.
-Введ. 01.07.84.
26. ГОСТ 12.1.012-90.ССБТ. Вибрация. Общие требования безопасности.
-Введ. 01.07.87.
27. ГОСТ 14254-80. Электрооборудование напряжением до 1000 В. Оболочки. Степени защиты. -Введ. 01.01.81.
28. ГОСТ 12.2.007.0-75 .ССБТ. Изделия электротехнические. Общие требования безопасности. -Введ. 01.01.78.
29. ГОСТ 12.1.030-81 .ССБТ. Электробезопасность. Защитное заземление. Зануление. -Введ. 01.07.82.
30. ДБН. В.1.1.-7-2002.
31. ГОСТ 12.1.004-91.ССБТ. Пожарная безопасность. Общие требования.
-Введ. 01.07.92.
32. ДСТУ 3008-95. Державний стандарт України. Документація. Звіти у сфері науки і техніки. Структура і правила оформлення.
33. СТВУЗ-ХПІ-2.01-2003. Система стандартів з організації навчального процесу. Дипломні роботи. Загальні вимоги. -Введ. 19.02.03.
34. СТВУЗ-ХПІ-2.03-2003. Система стандартів з організації навчального процесу. Дипломні науково-дослідні роботи. Порядок виконання. –Введ. 19.02.03.
Додаток А
На рисунку А.1 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- не в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 1.
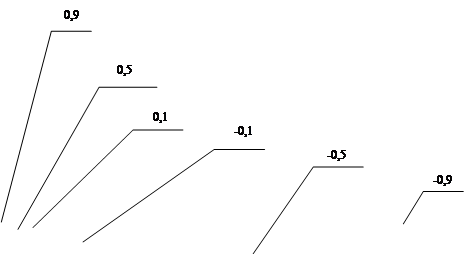
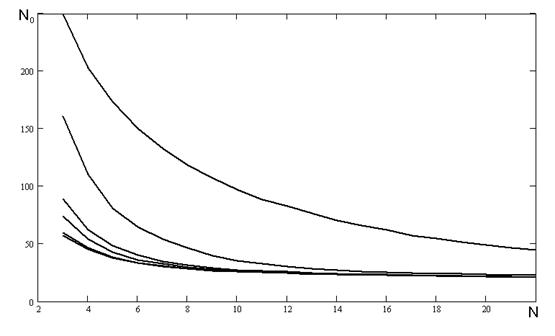
Рисунок А.1 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.2 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- не в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 2.
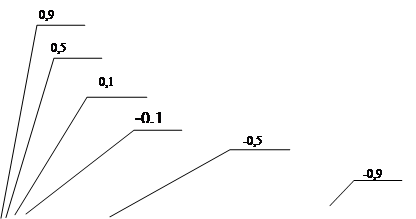
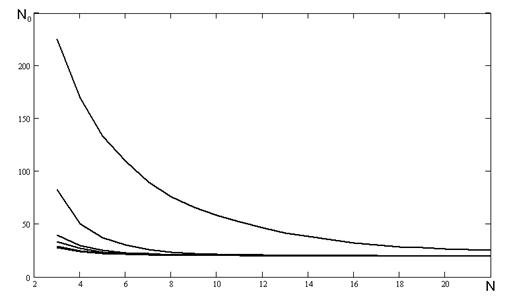
Рисунок А.2 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.3 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 1.

 Рисунок А.3 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.3 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.4 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 2.
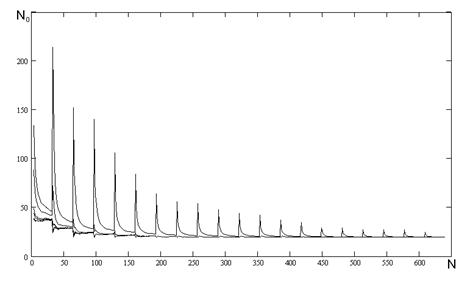
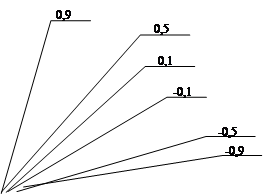 Рисунок А.4 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.4 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.5 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 1.
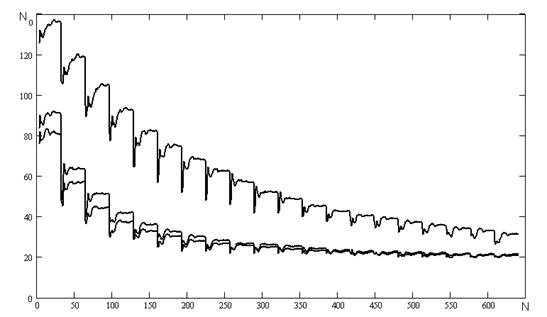
 Рисунок А.5 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.5 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
Алгоритм НК з використанням сімейства фільтрів МА(1).
На рисунку А.6 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- не в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 1
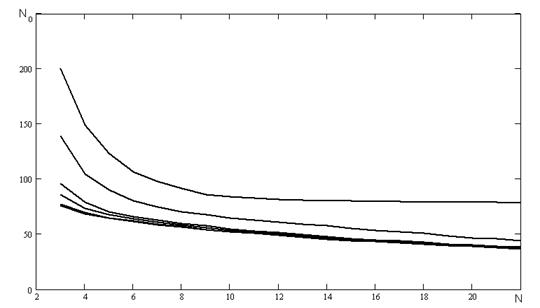
 Рисунок А.6 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.6 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.7 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- не в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 2
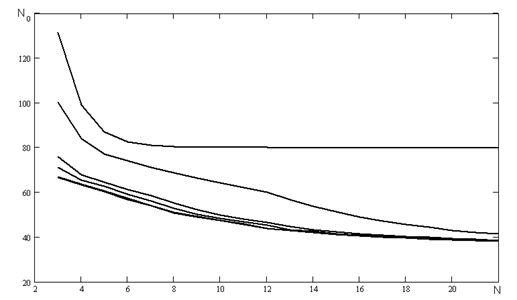
 Рисунок А.7 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.7 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.8 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 1
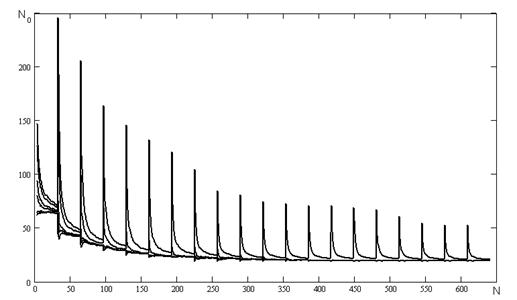
 Рисунок А.8 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.8 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.9 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 2
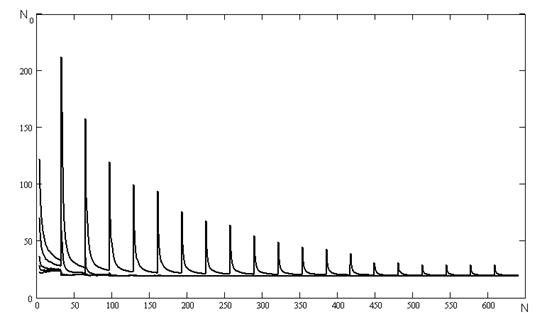
 Рисунок А.9 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.9 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.10 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 1

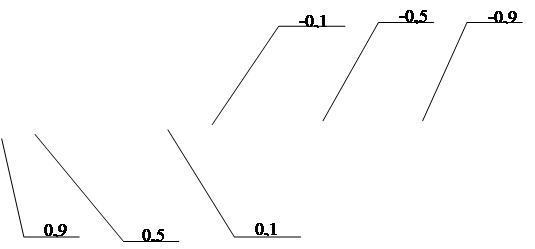 Рисунок А.10 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.10 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.11 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 2
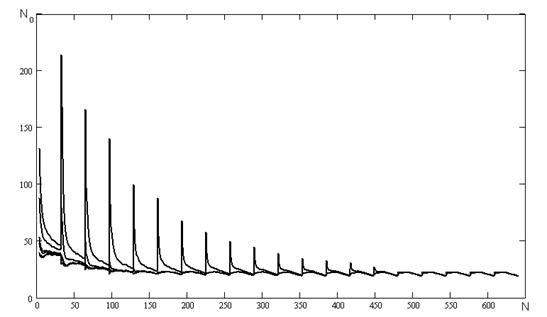
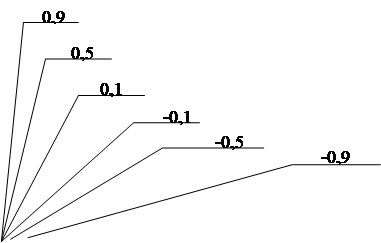 Рисунок А.11 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.11 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.12 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- не в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 1
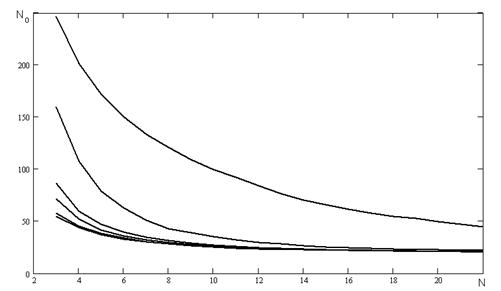
 Рисунок А.12 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.12 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
На рисунку А.13 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:
- не в кожному інтервалі відбувається обчислення коефіцієнту а;
- початкове значення коефіцієнту ![]() ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
ініціалізується наступними значеннями: 0,1, 0,5, 0,9, -0,1, -0,5, -0,9;
- співвідношенні сигнал/шум було обрано наступним Soot = 2
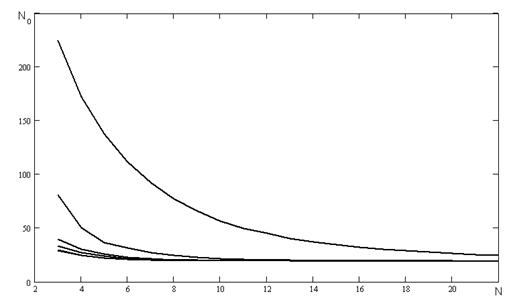
 Рисунок А.13 - Залежність кількості перетинів нульового рівня від частоти.
Рисунок А.13 - Залежність кількості перетинів нульового рівня від частоти.
Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.
0 комментариев