Параметричний фільтр МА(1)

4.4 Параметричний фільтр МА(1)

Фільтр МА(1) задовольняє фундаментальній властивості відносно білого шуму (4.10). МА(1) – сімейство подібно до  - фільтру.

Нехай наша модель буде (4.1) з {Z_t}, стаціонарною з нульовим середнім Гаусовими часовими рядами, визначеними як:

, (4.11)

де , ми обмежуємо  для зручності.

Вважаємо сімейство {L_r} ковзного згладжування першого порядку МА(1), фільтрів , що індексується параметром r,  і визначається як:

, (4.12)

і піднесений до квадрату коефіцієнт передачі  є

, (4.13)

де ,

Це сімейство складається з простого з імпульсним відкликом фільтром, який демонструє характеристики фільтру нижніх частот для відповідних значень параметра r, який позитивний і демонструє характеристики фільтру високих частот для негативних значень параметру.

Фундаментальна властивість вимагає щоб [15]:

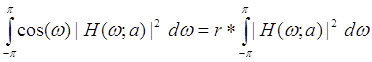, (4.14)

оскільки нам потрібно щоб шум був білий. Але обчислення невласного інтегралу дає [15]:

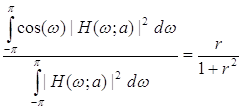, (4.15)

Таким чином нам потрібна репараметризація. Для отримання ре параметризації, яка задовольняє фундаментальній властивості, водимо параметр:

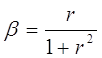(4.16)

та роз’язуємо відносно r:

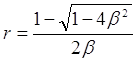(4.17)

Таким чином, вимога фундаментальної властивості задовольняється сімейством, що було репараметризовано за допомогою . Зазначимо, що , тому є привід обмежити .

Наступні експерименти були проведені з метою з’ясування можливостей алгоритму НК з використанням сімейств фільтрів МA(1), визначення кількості перетинів нульового рівня корисним сигналом, що складається з однієї гармоніки постійної за параметрами на всій довжині вхідної послідовності.

Далі буде показана реалізація алгоритму HK з використанням фільтру МA(1). Реалізація цього алгоритми була виконана з наступними параметрами:

- N = 20 – кількість проходів по вхідної послідовності;

- N = 32 – кількість інтервалів, на яку розбивається вхідна послідовність;

- D – число перетинів нуля на попередніх інтервалах;

- кількість точок на одному інтервалі N_i дорівнює 512;

- кількість періодів синусоїди в одному інтервалі дорівнює 10 і відповідно кількість перетинів нульового рівня – 20;

- загальна довжина вхідної послідовності дорівнює 16384 точок;

- точок відліку на один період припадає 51;

- 1024 точкам відліку у часовому вимірі відповідає 1 секунда;

- частота синусоїди дорівнює 20.0784 Гц;

- загальна довжина вхідної послідовності 16 секунд;

- кількість перетинів нуля вхідної послідовності 639.

Для проведення експерименту по виявленню корисного сигналу на фоні завади, була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Перед використанням алгоритму HK з фільтру МA(1) попередньо синусоїду з відомими параметрами змішуємо з отриманим шумом.

На одному графіку будуть показані результати експериментів з ініціалізацією початкового значення параметру  наступними значеннями 0,1, 0,5, 0,9.

За для зручності аналізу отриманих результатів було прийнято рішення подавати результати на двовимірному графіку через те, що на тривимірному графіку важко порівнювати різні експерименти. Кожен графік буде подавати інформацію про експерименти з одним співвідношення але з різними початковими значеннями параметру .

Описані експерименти проводилися для двох різновидів алгоритмів HK з використанням фільтру сімейства AR(1).

У першому варіанті алгоритму проводилася зміна поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру  після кожного інтервалу вхідної послідовності.

У другому варіанті алгоритму проводилася зміна поточної кількості перетинів нульового рівня вхідним сигналом, на протязі двадцяти ітерацій, з новим обчисленням параметру  після проходження усієї вхідної послідовності.

З метою отримання моделі завади була використана стандартна функція пакету Mathcad 2001 для отримання шуму з потрібними параметрами. Її амплітуда при генерації задавалася за допомогою стандартного математичного відхилення. Для порівняння амплітуди синусоїди з завадою використовувалося діюче значення амплітуди сигналу синусоїди.

На рисунку 4.8 наведені результати числових експериментів проведених з наступними початковими умовами та початковими ініціалізаціями параметрів:

- не в кожному інтервалі відбувається обчислення коефіцієнту а;

- початкове значення коефіцієнту  ініціалізується наступними значеннями: 0,1, 0,5, 0,9;

- співвідношенні сигнал/шум було обрано наступним Soot = 1.

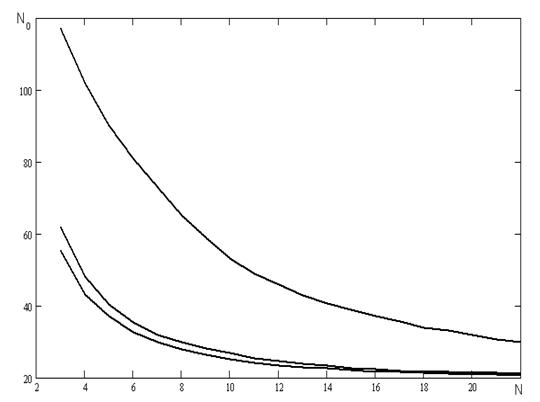
Рисунок 4.8 - Залежність кількості перетинів нульового рівня від частоти.

Використаний генератор псевдовипадкових чисел з пакету Mathcad 2001.

Алгоритм НК з використанням сімейства фільтрів МА(1).

Експерименти з іншими параметрами наведені в додатку А на рисунках А.5.

З наведених результатів експериментів можна зробити висновки стосовно того, що використання сімейства фільтрів МА(1) дає трохи гірші результати.