Визначення кількості перетинів корисного сигналу з нульовим рівнем за допомогою методики для квантованого у часі сигналУ

4 Визначення кількості перетинів корисного сигналу з нульовим рівнем за допомогою методики для квантованого у часі сигналУ

4.1 Визначення дискретної частоти за допомогою перетинів нульового значення

В даному розділі будуть наведені методи ті, що використовують ітеративні фільтраційні процедури для визначення частот сигналів, схованих у шумі компонент. Подана методика використовує параметричну фільтрацію для рекурсивного визначення частот дискретних спектральних компонент.

Визначення частоти – класична задача аналізу часових рядів. Майже сотні років періодограми широко застосовувалися для аналізу та визначення спектрів. Швидке перетворення Фур’є (FFT), що являє собою ефективний алгоритм для оцінки періодограм у частотах Фур’є, підтримує популярність цього важливого інструмента. Але на протязі більш ніж десяти останніх років багато авторів пропонували методи ітеративної фільтрації для визначення частот дискретних гармонік [8, 11-14].

Корисна математична модель, так саме, як і та, що ми використовуємо у цьому прикладі, це наступна суміш сигналів стаціонарного процесу,

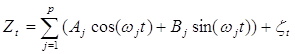, (4.1)

де,  - дискретні значення часу;

А та В всі не корельовано,  - математичне відхилення, та  - дисперсія.

Взагалі, приймаємо  - підкрашений стаціонарний шум з нульовим середнім значенням і дисперсією , незалежною від А та В. Шум, приймаємо, має абсолютно неперервну спектральну функцію  зі спектральною щільністю , . Для нашої мети ми приймаємо, що {Z_t} – Гаусів процес. Але Гаусовість не є необхідною для параметричної фільтрації за методом Яковітца [16]. Також покажемо, що частота для нас є низка упорядкованих констант в межах (0,) [15],

, (4.2)

Загальна задача це визначити частоти , використовуючи кінцеву довжину реалізації (спостереження) з часового ряду Z₁, Z₂, ...,Z_N.

Іншими словами, наша основна стратегія це фільтрувати спостереження Z₁, Z₂, ...,Z_N за допомогою фільтру з параметричного сімейства лінійних фільтрів, спостерігати статистику перетинів нуля виходу фільтру, а потім обирати інший фільтр (зміною параметра) з сімейства на базі статистики, що спостерігається. При деяких умовах ця ітеративна процедура сходиться і точне значення частоти може бути отримане.

4.2 Очікуване число перетинів нуля Гаусова процесу

Нижче подано формули для визначення очікуваної кількості перетинів нуля Гаусова процесу. Наведемо обидва випадки: безперервного та дискретного часу.

Якщо стаціонарний Гаусів процес {Z_t}, для , з нормалізованою автокореляційною функцією  має дуже гладку форму, що середнє число перетинів нуля за одиницю часу, дорівнює за формолою Райса [4].

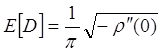, (4.3)

де D – число перетинів нуля у реалізації {Z_t} для t у одиничному інтервалі [0, 1];

є друга похідна нормалізованої автокореляційної функції від {Z_t} у нулі.

Ялвісакер в 1965 довів формулу Райса строго при пом’якшуючих умовах і показав, що очікувана кількість перетинів нулів скінченна якщо, і тільки якщо, автокореляційна функція двічі може бути диференційована в точці .

Аналогічна формула для дискретного часу, для процесу з нульовим середнім, для стаціонарної Гаусової послідовності {Z_к},  була отримана багатьма авторами [7] і виглядає як:

, (4.4)

або, еквівалентно, в інверсній формі:

, (4.5)

де D₁ – число змін знаків або перетинів нуля у реалізаціях Z₁, ...,Z_N;

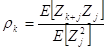 - кореляція послідовності {Z_к};

 - очікувана число перетинів нуля при дискретному часі.

Ця формула (4.5) має назву – косинусна формула. Спостерігаємо, що через стаціонарність очікуване число перетинів нуля  - не залежить від N. Взагалі  повинен бути кореляцією, див. Кедем (1991). Оскільки лінійна фільтрація Гаусова процесу дає результат Гаусів процес, косинусна формула придатна для фільтрованого процесу, де кореляційний коефіцієнт і число перетинів нуля фільтрованого процесу використано у косинус ній формулі (4.5). Для точності, нехай  буде вихід у момент t з лінійного з незмінними у часі параметрами фільтру L_a, що був застосований до процесу {Z_t}. Використовуючи косинусну формулу (4.5) і спектральне подання для стаціонарних процесів, коефіцієнти кореляції першого порядку  фільтрованого процесу  отримаємо вираз [15]:

, (4.6)

де D_a – число перетинів нуля в {L_a(Z)₁, ...,L_a(Z)_N,};

- функція спектрального розподілу процесу {Z_t};

 - квадрат коефіцієнту передачі фільтру L_a.

Перетини нуля D_a фільтрованого часового ряду називаємо “Перетини вищого порядку” або НОС [7].

Для даного з нульовим середнім часового ряду {Z_к} і сімейства параметричних фільтрів з пространством параметрів , , відповідає НОС сімейство помічено як .