Навигация
Алгебраическое представление логической функции в СДНФ
2. Алгебраическое представление логической функции в СДНФ
![]()
![]()
3. Алгебраическое представление логической функции в СКНФ
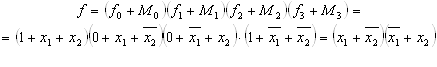
Ускорить процесс нахождения СДНФ и СКНФ можно, если применить другие правила.
СДНФ находят по правилу записи логической функции “по единицам”:
выписывают ряд произведений всех аргументов и соединяют их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в единицу;
записывают под каждым произведением набор аргументов, на котором функция равна единице, и над аргументами равными 0, ставят знаки отрицания.
Пример 1.2. Представить в СДНФ логическую функцию пяти аргументов f(x1,x2,x3,x4,x5), равную единице на следующих четырех наборах
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Решение. 1. Запишем четыре произведения аргументов, связанных знаком дизъюнкции, и под каждым из них - один из перечисленных наборов
| x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 |
| 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 |
2. Расставляя отрицания над аргументами, равными нулю, получим СДНФ логической функции:
![]() Ú
Ú ![]() Ú
Ú ![]() Ú
Ú ![]()
СКНФ находят по правилу записи переключательной функции “по нулям”:
1) выписывают произведения дизъюнкций всех аргументов с количеством сомножителей, равным числу наборов, на которых заданная функция обращается в нуль;
2) записывают под каждым сомножителем набор аргументов, на котором функция равна нулю, а над аргументами, равными единице ставят знаки отрицания.
Пример 1.3. Представить в СКНФ переключательную функцию четырех аргументов f(x1,x2,x3,x4) , равную нулю на наборах
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Решение. 1. Запишем четыре произведения дизъюнкций всех аргументов и под каждым из них один из перечисленных наборов:
| (x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) |
| 0 0 1 1 0 1 1 1 1 0 0 0 1 1 1 1 |
2. Расставляя знаки отрицания над аргументами, равными единице, получим СКНФ логической функции:
![]()
При выборе совершенной формы записи логической функции следует иметь в виду, что СДНФ является более целесообразной, если число наборов, на которых функция равна 0, превышает число наборов, на которых функция равна 1. В противоположном случае более приемлемой будет СКНФ.
Пример 1.4. Необходимо построить мажоритарную ячейку (ячейку голосования) на три входа, т.е. такую ячейку, у которой сигнал на выходе равен единице тогда, когда большинство входных сигналов равно единице, т.е. он равен единице, когда на двух или трех входах присутствует сигнал единицы, в противном случае выходной сигнал равен нулю [2].
Представить логическую функцию мажоритарной ячейки в виде таблицы истинности и в алгебраическом виде в формах СДНФ и СКНФ.
Решение. 1. Для трех входных сигналов, т.е. для n=3 переменных существует q=2n=23=8 различных комбинаций этих сигналов табл.1.4.
Таблица 1.4
Таблица истинности
| x1 | x2 | x3 | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2. Для представления логической функции в алгебраическом виде в форме СДНФ нужно представить эту функцию в виде суммы логических произведений аргументов, соответствующих тем строкам таблицы истинности, для которых логическая функция равна единице. При записи этих логических произведений следует брать соответствующий аргумент с инверсией, если этот аргумент в данной строке таблицы равен нулю, и без инверсии, если он равен единице:
![]()
3. Для представления логической функции в алгебраическом виде в форме СКНФ нужно представить эту функцию в виде произведения логических сумм аргументов, соответствующих тем строкам таблицы истинности, для которых логическая функция равна нулю. При записи этих логических сумм следует брать соответствующий аргумент с инверсией, если этот аргумент в данной строке таблицы равен единице, и без инверсии, если он равен нулю:
![]()
Пример 1.5. Полный набор ![]() = 16 логических функций двух переменных приведен в табл.1.5. Записать алгебраические выражения этих функций в формах СДНФ и СКНФ.
= 16 логических функций двух переменных приведен в табл.1.5. Записать алгебраические выражения этих функций в формах СДНФ и СКНФ.
Таблица 1.5
Полный набор логических функций двух переменных
| Таблица истинности | Название функции | Условное обозначение | Алгебраическое выражение | ||||||
| Функция | x1 | 0 | 0 | 1 | 1 | ||||
| x2 | 0 | 1 | 0 | 1 | СДНФ | СКНФ | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| f0 | 0 | 0 | 0 | 0 | Константа нуль | 0 | |||
| f1 | 0 | 0 | 0 | 1 | Конъюнкция | x1 x2 | |||
| f2 | 0 | 0 | 1 | 0 | Запрет по x2 | x1 x1 | |||
| f3 | 0 | 0 | 1 | 1 | Тождественность x1 | x1 | |||
| f4 | 0 | 1 | 0 | 0 | Запрет по x1 | x2 x2 | |||
| f5 | 0 | 1 | 0 | 1 | Тождественность x2 | x2 | |||
| f6 | 0 | 1 | 1 | 0 | Исключающее ИЛИ Сумма по модулю 2 | x1 | |||
| f7 | 0 | 1 | 1 | 1 | Дизъюнкция | x1 Ú x2 x1 + x2 | |||
| f8 | 1 | 0 | 0 | 0 | Стрелка Пирса | x1 ¯ x2 | |||
| f9 | 1 | 0 | 0 | 1 | Равнозначность | x1 ~ x2 | |||
| f10 | 1 | 0 | 1 | 0 | Инверсия x2 |
| |||
| f11 | 1 | 0 | 1 | 1 | Импликация от x2 к x1 | x2 ® x1 | |||
| f12 | 1 | 1 | 0 | 0 | Инверсия x1 |
| |||
| f13 | 1 | 1 | 0 | 1 | Импликация от x1 к x2 | x1 ® x2 | |||
| f14 | 1 | 1 | 1 | 0 | Штрих Шеффера | x1 / x2 | |||
| f15 | 1 | 1 | 1 | 1 | Константа единицы | 1 | |||
Логическая функция может быть представлена графически в виде карт минтермов - карт Карно.
Логическую функцию предварительно, исходя из таблицы истинности, приводят к совершенной дизъюнктивной нормальной форме (СДНФ):
![]() ,
,
Где fi, mi - значение функции (0 или 1) и минтерм, соответствующий i-ому набору переменных.
Минтерм - конъюнкция переменных, которые входят либо в прямом виде, если значение данной переменной в наборе равно 1, либо в инверсном виде, если значение переменной равно 0.
Минтерм - это простая конъюнкция, в которую входят все аргументы рассматриваемой логической функции [3].
Простой конъюнкцией считается логическое произведение переменных, взятых с отрицаниями или без них, в котором каждая переменная встречается не более одного раза (в простую конъюнкцию не должны входить суммы переменных, отрицания функций двух или нескольких переменных).
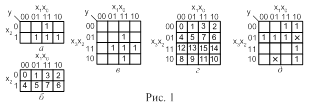
После представления функции в СДНФ, следует заполнить прямоугольную таблицу, в которой число клеток равно числу возможных минтермов. Эту таблицу называют диаграммой Вейча или картой Карно. Каждой клетке таблицы ставится в соответствие определенная конъюнкция так, чтобы в соседних клетках (снизу и сверху, слева и справа) конъюнкции отличались не более чем одним сомножителем. Для этого нумерацию столбцов и строк таблицы ведут кодом Грея, количество разрядов которого равно количеству переменных, отведенных для строк и столбцов.
При заполнении таблицы в соответствующую клетку ставится 1, если логическая функция при данном наборе аргументов равна единице(рис.1.1-1.4).
| x1 x2 | 0 | 1 |
| 0 |
|
|
| 1 |
|
|
Рис.1.1 Карта Карно для логической функции двух аргументов.
| x1x2 x3 | 00 | 01 | 11 | 10 |
| 0 |
|
|
|
|
| 1 |
|
|
|
|
Рис.1.2 Карта Карно для логической функции трех аргументов.
| x1x2 x3x4 | 00 | 01 | 11 | 10 |
| 00 |
|
|
|
|
| 01 |
|
|
|
|
| 11 |
|
|
|
|
| 10 |
|
|
|
|
Рис. 1.3 Карта Карно для логической функции четырех аргументов.
| x1x2x3 x4x5 | 000 | 001 | 011 | 010 | 110 | 111 | 101 | 100 |
| 00 | ||||||||
| 01 | ||||||||
| 11 | ||||||||
| 10 |
Рис.1.4 Карта Карно для логической функции пяти переменных.
Между представлением логической функции в табличной (таблица истинности), алгебраической (в виде СДНФ) и графической (на карте Карно) формах имеется однозначное соответствие. Логическая функция на карте Карно представляется совокупностью клеток, заполненных 1, инверсия этой функции представляется совокупностью пустых клеток (или заполненных 0).
Для логических функций с числом переменных n ³ 6 наглядность карт Карно теряется и поэтому такие функции представляются в виде композиции функции меньшего числа переменных:
![]() ,
,
где x1 - выделяемая переменная;
функции ![]() получаются из функции f подстановкой значений x1=0 и x1=1.
получаются из функции f подстановкой значений x1=0 и x1=1.
В качестве выделяемой может использоваться любая переменная. Например,
![]()
![]()
Процесс выделения более простых функций называется декомпозицией. Полученные функции f0 и f1 могут подвергаться дальнейшей декомпозиции.
1.2 Логические операции
Множество логических функций n переменных можно образовать посредством трех основных логических операций:
1) Логическое отрицание (инверсия);
2) Логическое сложение (дизъюнкция);
3) Логическое умножение (конъюнкция).
Более сложные логические преобразования можно свести к указанным операциям [4]. Логические функции подчиняются принципу дуальности (двойственности) - теоремы Де Моргана; согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять логическую 1 на 0, 0 на 1, знак Ú (+) на Ù(×), а Ù(×) на Ú (+), где Ú или + - обозначение операции дизъюнкции; Ù или × - обозначение операции конъюнкции.
1.3 Аксиомы булевой алгебрыБулева алгебра базируется на нескольких аксиомах, из которых выводят основные законы для преобразований с двоичными переменными (табл. 1.6, 1.7)
Таблица 1.6Аксиомы булевой алгебры
| конъюнкция | дизъюнкция | |
| 0×0=0 | 0+0=0 | |
| 0×1=0 | 0+1=1 | |
| 1×1=1 | 1+1=1 | |
| x×0=0 | x+0=x |
| x×1=x | x+1=1 |
| x×x=x | x+x=x |
|
|
|
Таблица 1.7
Законы булевой алгебры
| Закон булевой алгебры | Конъюнкция | Дизъюнкция |
| 1 | 2 | 3 |
| Переместительный (коммутативности) | x1 x2 = x2 x1 | x1+ x2 = x2 + x1 |
| Сочетательный (ассоциативности) | x1 x2 x3 = x1 (x2 x3) = (x1 x2)x3 | x1+x2 +x3 = (x1+x2)+x3= =x1 +(x2+x3) |
| Распределительный (дистрибутивности) | x1(x2 +x3)= x1 x2 +x1 x3 | x1+(x2x3)= (x1+x2)(x1+x3) |
| Поглощения | x1+x1 x2 = x1 | x1 (x1+x2) = x1 |
| Склеивания |
|
|
| Де Моргана (инверсии, дуальности) |
|
|
| Развертывания |
|
|
| Не полного |
|
|
![]()
![]()
![]()
![]()
При минимизации логических функций в карте Карно обводят прямоугольными контурами все единицы и затем записывают минимизированную функцию в виде суммы логических произведений, описывающих эти контуры.
При проведении контуров придерживаются правил:
1) контур должен быть прямоугольным;
2) внутри контура должны быть только клетки, заполненные единицами;
3) число клеток, находящихся внутри контура, должно быть целой степенью числа 2, т.е. можно склеивать 1, 2, 4, 8,... членов;
4) одни и те же клетки, заполненные единицами, могут входить в несколько контуров;
5) при проведении контуров самая нижняя и самая верхняя строки таблицы считаются соседними, то же - для крайнего левого и крайнего правого столбцов;
6) число контуров должно быть как можно меньшим, а сами контуры как можно большим.
Пример 1.6. Провести минимизацию логической функции, заданной в форме СДНФ,с помощью карты Карно (рис.1.5).
![]()
| x1x2 x3 | 00 | 01 | 11 | 10 |
| 0 |
| 1 | ||
|
| 1 | 1 | 1 |
Рис.1.5 Карта Карно.
Решение. С помощью преобразований, выполняемых по законам булевой алгебры, и с учетом объединенных на карте Карно клеток, получают минимизированное выражение (МДНФ) логической функции:
![]()
![]()
![]() ;
;
![]()
![]() ,
,
![]()
![]() .
.
В рассмотренном примере двум клеткам первого объединения соответствуют минтермы, имеющие две общие переменные
![]() .
.
Поэтому дизъюнкция этих минтермов равна этим двум общим переменным: ![]() .
.
Четырем клеткам второго объединения соответствуют минтермы имеющие одну общую переменную ![]() :
:
![]()
Дизъюнкция этих минтермов также равна общей переменной ![]() .
.
Чем больше клеток входит в объединение, тем меньше переменных входит в соответствующий конъюнктивный член, т.е. проще МДНФ.
Процесс получения алгебраического выражения логической функции, представленной на карте Карно, сводится к считыванию объединений клеток. При этом каждое объединение клеток считывают в виде конъюнктивного члена, в который входят переменные или их инверсии, общие для всех минтермов, соответствующих этим клеткам.
Необъединенные клетки считывают в виде записанных в них минтермов.
Число конъюнктивных членов в МДНФ равно сумме объединений и необъединенных клеток.
Пример 1.7. Логическая функция задана табл.1.8
Таблица 1.8Таблица истинности
| x1 | x2 | f |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Найти СДНФ этой функции, и провести минимизацию с помощью карты Карно.
Решение: 1. Находят минтермы:
| x1 | x2 | mi | f |
| 0 | 0 |
| 1 |
| 0 | 1 |
| 1 |
| 1 | 0 |
| 0 |
| 1 | 1 |
| 1 |
2. Логическая функция в форме СДНФ:
![]() .
.
3. Карта Карно логической функции (рис.1.6)
| x1 x2 | 0 | 1 |
|
| 1 | |
| 1 |
| 1 |
Рис.1.6 Карта Карно логической функции
Похожие работы
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... порядка рис.7,б, которая хуже схемы рис.7,а по характеристикам быстродействия и сложности. Ухудшение характеристик оправдывается только возможностью реализации схемы на заданных стандартных элементах. 8. Комбинационные схемы Логическая схема (рис.8) с n входами и k выходами реализует систему переключательных функций y0 ...yk-1. Каждая функция yi(x0 ...xk-1) однозначно соответствует ...
... одно состояние из множества А, каждой строке – один входной сигнал из множества Z. На пересечении строки и столбца в таблице переходов, записывается состояние as, в которое должен перейти автомат из состояния am, под действием входного сигнала zf, т.е. as = σ(am, zf). На пересечении строки и столбца в таблице выходов записывается выходной сигнал wg, выдаваемый автоматом в состоянии am при ...
... к утверждению выводимости формулы Применение логики высказываний к анализу математических доказательств Ни у кого не возникает сомнения в том, что математические доказательства являются примерами строгих логических рассуждений. Аппарат логики высказываний позволяет нам прояснить структуру доказательств многих математических утверждений. Рассмотрим с точки зрения логики высказываний ...
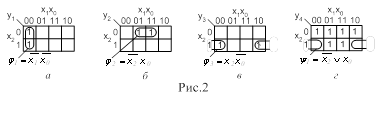
0 комментариев