Алгебраическое представление логической функции в СДНФ
Получают МДНФ функции
Строят для заданной функции импликантную матрицу (табл.1.9)
Макстермная матрица задана табл.1.11
Функциональная схема для функции, представленной в СКНФ, в базисе И, ИЛИ, НЕ (рис.3.3)
Двоично-десятичный код 2421 соответствует представлению числа в виде
Функциональная схема устройства на рис.5.7
Получают логическую функцию шифратора в виде СДНФ путем записи "по единицам"
Синтезируют полусумматор на элементах И, ИЛИ, НЕ (рис.5.18)
Функциональная схема полного сумматора, синтезированного из двух полусумматоров (рис. 5.21)
Навигация
Синтезируют полусумматор на элементах И, ИЛИ, НЕ (рис.5.18)
Основы анализа и синтеза комбинационных логических устройств
75776
знаков
73
таблицы
44
изображения
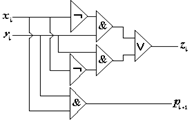
3. Синтезируют полусумматор на элементах И, ИЛИ, НЕ (рис.5.18).
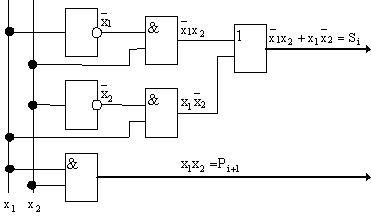
Рис.5.18 Полусумматор на элементах И, ИЛИ, НЕ
4. Для синтеза схемы на элементах И-НЕ используют основное соотношение булевой алгебры: 
, поэтому
.
Применяют закон Де Моргана:
.
Равенство не изменится, если к сомножителю 
прибавить 
, а к сомножителю 
- 
, т.к. 
, 
:
,
.
Вновь применяют закон Де Моргана:
,
.
Полученные соотношения подставляют в исходное выражение:
.
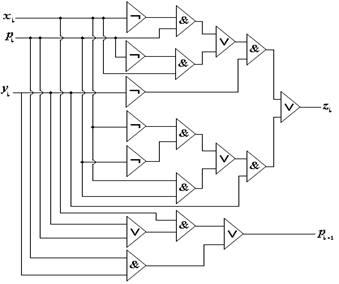
5. Функциональная схема сумматора на элементах И-НЕ (рис. 5.19).
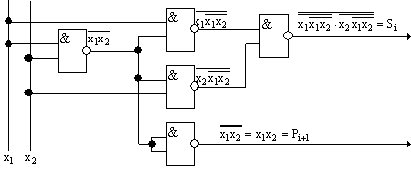
Рис. 5.19 Сумматор на элементах И-НЕ
6. Для синтеза схемы на элементах ИЛИ-НЕ представляют логическую функцию в форме СКНФ путем записи “по нулям”:
7. Проводят преобразование
8. Функциональная схема полусумматора на элементах ИЛИ-НЕ (рис.5.20).
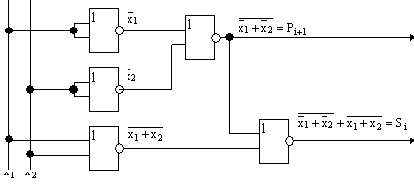
Рис.5.20 Полусумматор на элементах ИЛИ-НЕ
Схемы на элементах ИЛИ-НЕ и И-НЕ оказалась проще - содержит 5 логических элементов, а на элементах И, ИЛИ, НЕ - 6.
Пример 5.6. Составить схему полного сумматора, используя полусумматоры.
Решение 1. Полный сумматор осуществляет сложение трех цифр: двух цифр 
и 
, принадлежащих одному разряду складываемых чисел, а также цифры переноса из предыдущего разряда 
. В результате суммирования этих трех цифр получается сумма 
и цифра переноса в старший разряд 
. Таким образом, это устройство с тремя входами и двумя выходами.
Полусумматоры имеют два входа для 
и , и два выхода для и .
В соответствии с сочетательным законом:
т.е. можно сначала сложить две цифры 
и
, а затем к промежуточной сумме 
прибавить .
Поэтому полный сумматор можно представить как объединение двух полусумматоров.
Первый полусумматор служит для сложения двух цифр и и обеспечивает выход промежуточной суммы 
и переноса 
.
Второй полусумматор складывает промежуточную сумму 
с цифрой переноса из предыдущего разряда , формирует перенос 
и сумму . При этом
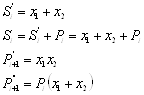
Из анализа таблицы истинности для полусумматора следует, что при сложении трех цифр двумя полусумматорами цифра переноса может образоваться только в одном полусумматоре: или . Поэтому для получения эти переносы следует объединить логической ячейкой ИЛИ:
.
Это выражение совпадает с полученным ранее для полного сумматора.
Похожие работы
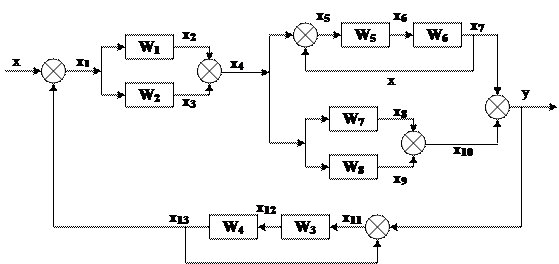
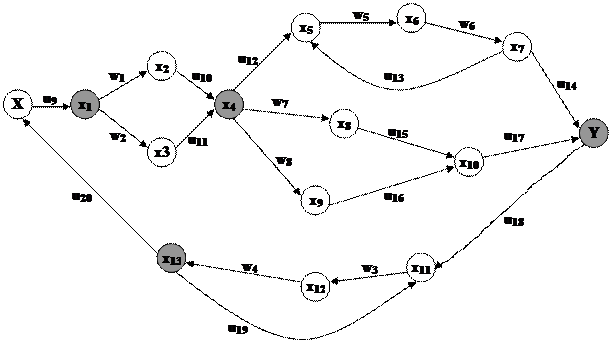
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... порядка рис.7,б, которая хуже схемы рис.7,а по характеристикам быстродействия и сложности. Ухудшение характеристик оправдывается только возможностью реализации схемы на заданных стандартных элементах. 8. Комбинационные схемы Логическая схема (рис.8) с n входами и k выходами реализует систему переключательных функций y0 ...yk-1. Каждая функция yi(x0 ...xk-1) однозначно соответствует ...
... одно состояние из множества А, каждой строке – один входной сигнал из множества Z. На пересечении строки и столбца в таблице переходов, записывается состояние as, в которое должен перейти автомат из состояния am, под действием входного сигнала zf, т.е. as = σ(am, zf). На пересечении строки и столбца в таблице выходов записывается выходной сигнал wg, выдаваемый автоматом в состоянии am при ...
... к утверждению выводимости формулы Применение логики высказываний к анализу математических доказательств Ни у кого не возникает сомнения в том, что математические доказательства являются примерами строгих логических рассуждений. Аппарат логики высказываний позволяет нам прояснить структуру доказательств многих математических утверждений. Рассмотрим с точки зрения логики высказываний ...
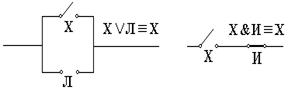
0 комментариев