Навигация
Получают логическую функцию шифратора в виде СДНФ путем записи "по единицам"
2. Получают логическую функцию шифратора в виде СДНФ путем записи "по единицам"
![]()
![]()
![]()
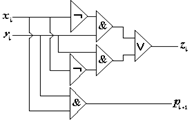
3. Функциональная схема шифратора в логическом базисе И-НЕ (рис.5.9.а) и в логическом базисе И, ИЛИ, НЕ (рис.5.9.б).
а). 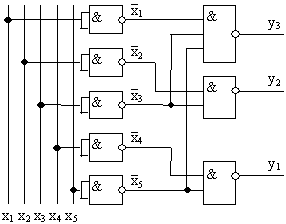
б) 
Рис. 5.9 Функциональная схема шифратора в логическом базисе И-НЕ (а) и в логическом базисе И, ИЛИ, НЕ (б)
5.6 Преобразователи кодовПреобразователи кодов используют для шифрации и дешифрации цифровой информации и имеют n входов и m выходов. Соотношения между числами n и m могут быть любыми: n<>m.
5.7 Сумматоры
Сумматоры - это комбинационные устройства, осуществляющие суммирование чисел в двоичном коде.
Правила суммирования в простейшем случае - суммирования двух одноразрядных чисел, задаются таблицей двоичного сложения:
0+0=0
0+1=1
1+0=1
1+1=0+единица переноса в старший разряд.
Логическую функцию одноразрядного суммирования составляют на основании правил суммирования (табл. 5.11)
Таблица 5.11
Таблица истинности сумматора
Слагаемые | Результат суммирования | ||
| х1 | х2 | Si | Цифра переноса в старший разряд, рi+1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Для получения логической функции одноразрядного суммирования в форме СДНФ производят запись " по единицам":
![]() ,
,
![]() ,
,
т.е. она реализуется двумя логическими функциями, а устройство имеет два выхода: Si и рi+1.
Схему, реализующую две функции, можно представить как простое объединение схем, реализующих каждую функцию отдельно, рис. 5.9:

Рис. 5.9 Функциональная схема одноразрядного сумматора: полусумматора.
Устройство оказывается синтезированным из двух самостоятельных частей, реализующих:
1) функцию исключающее ИЛИ (сумма по модулю два);
2) функцию конъюнкции И.
Такое устройство называется полусумматором.
Полный одноразрядный сумматор должен иметь вход для цифры переноса из предыдущего разряда рi и число слагаемых в нем оказывается равным трем: х1, х2, рi (табл.5.12). Логическую функцию для полного одноразрядного сумматора представляют таблицей истинности, составленной на основании правил суммирования.
Таблица 5.12
Таблица истинности полного одноразрядного сумматора
| Слагаемые | Результат суммирования | |||
| Цифра переноса из предыдущего Разряда рi | Первое слагаемое x1 | Второе Слагаемое x2 | Сумма Si | Цифра переноса в старший разряд, pi+1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Для получения логической функции в алгебраической форме в виде СДНФ производят запись по "единицам":
![]()
![]() ,
,
Далее производят минимизацию логических функций. Выражение для Si не поддается минимизации изложенными ранее методами. Единственная возможность - это использовать вынесение за скобки:
![]()
Для выражения рi+1 можно получить сокращенную дизъюнктивную нормальную формы применив все операции склеивания и поглащения:
1-4: ![]() (по рi)
(по рi)
2-4: ![]() (по х2)
(по х2)
3-4: ![]() (по х1)
(по х1)
Сокращенная дизъюнктивная форма логической функции:
![]()
Таким образом, полный сумматор оказывается устройством с двумя выходами и реализуется двумя логическими функциями Si и Pi+1 с тремя аргументами x1, x2, P i.
Схему, реализующую несколько функций, можно представить как простое объединение схем, реализующих каждую функцию отдельно.
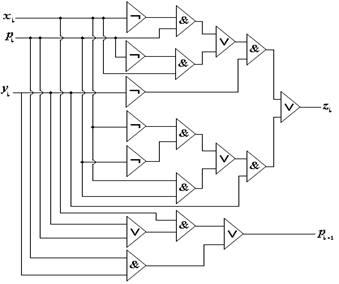
Функциональная схема в логическом базисе И, ИЛИ, НЕ на рис.5.10.


Рис.5.10 Функциональная схема полного одноразрядного сумматора.
Но такой путь, как правило, является неэкономичным. Схема оказалась реализованной на 16 базовых логических элементах.
Часто бывает целесообразно преобразовать совокупность данных логических функций к такому виду, чтобы реализующие их схемы содержали общие части, а схема с многими выходами представляла собой единое целое.
Поэтому продолжим преобразования.
На следующем этапе преобразований целесообразно более простую реализацию функции ![]() использовать в качестве составной части другой функции
использовать в качестве составной части другой функции ![]() . Для такой функции табл.5.13.
. Для такой функции табл.5.13.
Таблица 5.13
Таблица истинности полного одноразрядного сумматора
|
|
|
|
|
|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | ´ |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | ´ |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | ´ |
| 0 | 1 | 1 | 0 | ´ |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | ´ |
| 1 | 0 | 1 | 0 | ´ |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | ´ |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | ´ |
| 1 | 1 | 1 | 1 | 1 |
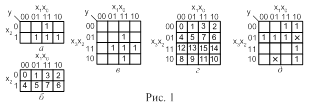
Но таблица истинности для ![]() теперь содержит избыточные наборы переменных, которые отмечены крестиками ´, т.е. функция оказывается частично (не полностью) определенной. Используем для минимизации частично определенной функции
теперь содержит избыточные наборы переменных, которые отмечены крестиками ´, т.е. функция оказывается частично (не полностью) определенной. Используем для минимизации частично определенной функции ![]() карту Карно (рис.5.11).
карту Карно (рис.5.11).
|
| 00 | 01 | 11 | 10 |
| 00 |
|
| 1 | |
| 01 | ´ | ´ | ´ | |
| 11 | ´ |
| ||
| 10 |
|
|
| ´ |
Рис.5.11 Карта Карно.
Минимальному покрытию соответствует логическая функция:
![]()
После вынесения за скобки ![]() получают подготовленную для реализации логическую функцию:
получают подготовленную для реализации логическую функцию:
![]()
Функциональная схема для этой логической функции в логическом базисе И, ИЛИ, НЕ показана на рис. 5.12.
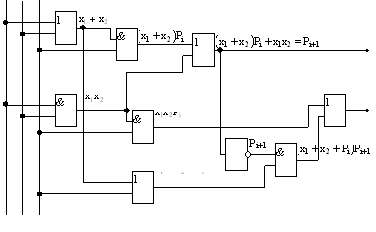
Рис.5.12 Минимизированная функциональная схема полного одноразрядного сумматора.
Схема оказалась реализованной на 9 базовых логических элементах, что почти в два раза меньше, чем в первой схеме. Это подтверждает целесообразность проведенных преобразований.
Для реализации схемы в базисах И-НЕ и ИЛИ-НЕ следует для логической функции применить формулу Де Моргана.
Получены схемы полных одноразрядных сумматоров.
Полные многоразрядные двоичные сумматоры составляются из одноразрядных.
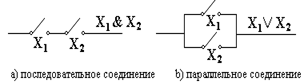
Способов выполнения сложения многоразрядных чисел два: параллельный и последовательный.
Процедуру сложения двух n-разрядных двоичных чисел ![]() можно представить рис.5.13.
можно представить рис.5.13.

Рис.5.13 Процедура сложения двух n-разрядных двоичных чисел
В младшем разряде сумматора используется полусумматор (два входа для ![]() и
и ![]() ).
).
Начиная со второго разряда необходимо иметь три входа: два для слагаемых ![]() и
и ![]() и один для сигнала переноса
и один для сигнала переноса ![]() с предыдущего разряда, т.е. необходимо применять полный сумматор.
с предыдущего разряда, т.е. необходимо применять полный сумматор.
Введем обозначения:
1) полного сумматора рис.5.14
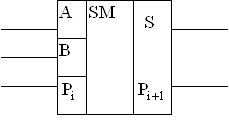
Рис.5.14 Обозначение на схеме полного сумматора
где S-выход суммы;
![]() - выход переноса;
- выход переноса;
![]() - вход переноса;
- вход переноса;
B - входы слагаемых цифр.
2) Полусумматора рис.5.15

Рис.5.15 Обозначение на схеме полу сумматора
В соответствии с рассмотренной схемой суммирования двух n-разрядных чисел схема n-разрядного сумматора может быть представлена в виде параллельного n-разрядного сумматора с последовательным переносом рис.5.16
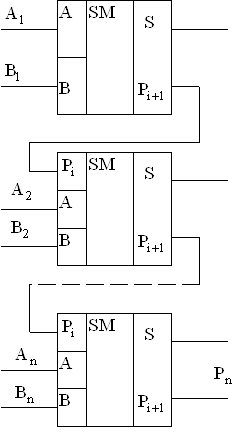
Рис.5.16 Параллельный n-разрядный сумматор
Число сумматоров здесь равно числу разрядов. Выход переноса ![]() каждого сумматора соединен с входом переноса
каждого сумматора соединен с входом переноса ![]() следующего, более старшего разряда. Слагаемые
следующего, более старшего разряда. Слагаемые ![]() и
и ![]() складываются во всех разрядах одновременно, а перенос
складываются во всех разрядах одновременно, а перенос ![]() поступает с окончанием операции сложения в предыдущем разряде.
поступает с окончанием операции сложения в предыдущем разряде.
Быстродействие параллельного многоразрядного сумматора с последовательным переносом ограниченно задержкой переноса, так как формирование сигнала переноса на выходе старшего разряда не может произойти до тех пор, пока сигнал переноса младшего разряда не распространится последовательно по всей системе [7].
Это устройство нетрудно сделать любой длины, однако суммирование будет закончено лишь тогда, когда истечет время распространения сигналов переноса ![]() через всю цепь одноразрядных сумматоров. Такой перенос иногда называют пульсирующим. При наиболее неблагоприятных условиях для распространения переноса при сложении чисел 11...11 и 00... 001, произойдет “пробег” 1 переноса через весь сумматор от самого младшего разряда к самому старшему. Поэтому в худшем случае время распространения переноса
через всю цепь одноразрядных сумматоров. Такой перенос иногда называют пульсирующим. При наиболее неблагоприятных условиях для распространения переноса при сложении чисел 11...11 и 00... 001, произойдет “пробег” 1 переноса через весь сумматор от самого младшего разряда к самому старшему. Поэтому в худшем случае время распространения переноса ![]() где
где![]() - время распространения переноса в одном разряде; n- число разрядов сумматора.
- время распространения переноса в одном разряде; n- число разрядов сумматора.
При последовательном суммировании используется один, общий для всех разрядов полный (рис.5.17).
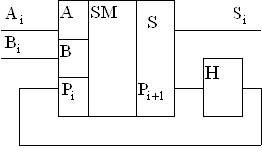
Рис.5.17 Сумматор с дополнительной цепью задержки
Оба слагаемых кодируются последовательностями импульсов, которые синхронно вводятся в сумматор через входы A и B, начиная с младших разрядов. Цепь задержки обеспечивает хранение импульса переноса ![]() на время одного такта, т.е. до прихода пары слагаемых следующего разряда, с которыми он будет просуммирован. Задержку обеспечивает D-триггер. Для хранения и ввода слагаемых A и B, а также для преобразования последовательного кода выходных импульсов
на время одного такта, т.е. до прихода пары слагаемых следующего разряда, с которыми он будет просуммирован. Задержку обеспечивает D-триггер. Для хранения и ввода слагаемых A и B, а также для преобразования последовательного кода выходных импульсов ![]() в параллельный применяют регистры сдвига. Работа регистров сдвига и триггера задержки синхронизируется общим генератором тактовых импульсов.
в параллельный применяют регистры сдвига. Работа регистров сдвига и триггера задержки синхронизируется общим генератором тактовых импульсов.
Последовательные многоразрядные сумматоры имеют сравнительно невысокое быстродействие, так как одновременно суммируется лишь пара слагаемых. При этом они состоят из трех регистров, одноразрядного сумматора, триггера задержки (D-триггера) и генератора тактовых импульсов.
Быстродействие параллельного многоразрядного сумматора можно увеличить, заменив последовательный перенос на параллельный перенос с помощью специального узла: схемы ускоренного переноса СУП.
Принцип ускоренного (сквозного, параллельного) переноса заключается в том, что для каждого двоичного разряда дополнительно формируют два сигнала:
1) образования переноса ![]()
2) распространения переноса ![]()
В случае ![]() , т.е.
, т.е. ![]() в данном i-ом разряде формируется сигнал переноса
в данном i-ом разряде формируется сигнал переноса ![]() в следующий высший разряд независимо от формирования функций суммы в предыдущих разрядах.
в следующий высший разряд независимо от формирования функций суммы в предыдущих разрядах.
Если хотя бы одно из слагаемых ![]() или
или ![]() равно 1 (т.е.
равно 1 (т.е. ![]() ), то перенос в последующий разряд произойдет при наличии сигнала переноса из предыдущего разряда.
), то перенос в последующий разряд произойдет при наличии сигнала переноса из предыдущего разряда.
Если функции распространения переноса в двух соседних разрядах равны 1, т.е. ![]() , и при этом существует сигнал переноса
, и при этом существует сигнал переноса ![]() из предыдущего разряда, то перенос производится непосредственно в разряд номер i+2.
из предыдущего разряда, то перенос производится непосредственно в разряд номер i+2.
Процесс формирования ускоренного переноса описывается следующим уравнением:
![]() .
.
Пример 5.5. Синтезировать узел, осуществляющий суммирование двух одноразрядных двоичных чисел (полусумматор), на элементах И, ИЛИ, НЕ, на элементах И-НЕ и на элементах ИЛИ-НЕ.
Решение. 1. Составляют таблицу истинности для логической функции одноразрядного суммирования на основании правил суммирования одноразрядных чисел (5.14).
Таблица 5.14
Таблица истинности
| Слагаемые | Результат суммирования | ||
|
|
| Сумма | цифра переноса в старший разряд |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
2. Представляют логическую функцию в форме СДНФ путем записи “по единицам”:
![]() ;
;
![]()
Похожие работы
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... порядка рис.7,б, которая хуже схемы рис.7,а по характеристикам быстродействия и сложности. Ухудшение характеристик оправдывается только возможностью реализации схемы на заданных стандартных элементах. 8. Комбинационные схемы Логическая схема (рис.8) с n входами и k выходами реализует систему переключательных функций y0 ...yk-1. Каждая функция yi(x0 ...xk-1) однозначно соответствует ...
... одно состояние из множества А, каждой строке – один входной сигнал из множества Z. На пересечении строки и столбца в таблице переходов, записывается состояние as, в которое должен перейти автомат из состояния am, под действием входного сигнала zf, т.е. as = σ(am, zf). На пересечении строки и столбца в таблице выходов записывается выходной сигнал wg, выдаваемый автоматом в состоянии am при ...
... к утверждению выводимости формулы Применение логики высказываний к анализу математических доказательств Ни у кого не возникает сомнения в том, что математические доказательства являются примерами строгих логических рассуждений. Аппарат логики высказываний позволяет нам прояснить структуру доказательств многих математических утверждений. Рассмотрим с точки зрения логики высказываний ...
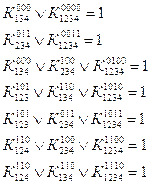
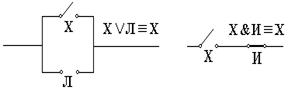
0 комментариев