Алгебраическое представление логической функции в СДНФ
Получают МДНФ функции
Строят для заданной функции импликантную матрицу (табл.1.9)
Макстермная матрица задана табл.1.11
Функциональная схема для функции, представленной в СКНФ, в базисе И, ИЛИ, НЕ (рис.3.3)
Двоично-десятичный код 2421 соответствует представлению числа в виде
Функциональная схема устройства на рис.5.7
Получают логическую функцию шифратора в виде СДНФ путем записи "по единицам"
Синтезируют полусумматор на элементах И, ИЛИ, НЕ (рис.5.18)
Функциональная схема полного сумматора, синтезированного из двух полусумматоров (рис. 5.21)
Навигация
Получают МДНФ функции
Основы анализа и синтеза комбинационных логических устройств
75776
знаков
73
таблицы
44
изображения
4. Получают МДНФ функции
.
Пример 1.8. Минимизировать с помощью карты Карно (рис.1.7) логическую функцию, заданную в форме СДНФ:
| x1x2 x3 | 00 | 01 | 11 | 10 |
| 0 |
| |||
| 1 |
| 1 | 1 |
1
1Рис.1.7 Карта Карно
Решение: МДНФ функции:
.
Пример 1.9. Минимизировать с помощью карты Карно (рис.1.8) заданную в форме СДНФ логическую функцию:
.
| x1x2 x3 | 00 | 01 | 11 | 10 |
| 0 |
|
| 1 |
|
| 1 | 1 | 1 |
1
1
1Рис.1.8 Карта Карно:
Решение: МДНФ функции:
Эти методы базируются на применении основных законов булевой алгебры.
Алгоритм получения МДНФ логической функции:
1. Логическая функция представляется в СДНФ. Причем, если она задана таблицей истинности, то представляют путем записи “по единицам”; если она задана алгебраической произвольной дизъюнктивной форме - путем применения операций развертывания, формул Де Моргана и др.
2. В полученном СДНФ проводят все возможные операции неполного склеивания и затем поглощения. В результате получают сокращенную дизъюнктивную нормальную форму, т.е. дизъюнкцию самых коротких из всех возможных элементарных произведений (простые импликанты), входящие в данную логическую функцию.
3. Находят минимальные дизъюнктивные нормальные формы по импликантной матрице.
Импликантная матрица - это таблица, на вертикальные и горизонтальные входы которой записывают соответственно члены СДНФ и простые импликанты заданной логической функции.
Клетки импликантной матрицы, образованные пересечением строк с импликантами и столбцов с поглощательными ими членами СДНФ, отмечают крестиками [5].
МДНФ находят как дизъюнкцию минимального числа импликант, которые совместно накрывают крестиками все колонки импликантной матрицы.
Пример 1.10. Минимизировать логическую функцию:
Решение: 1. Функция задана в алгебраической форме, применяя операции развертывания
получают СДНФ, содержащую шесть членов:
2. Операции склеивания проводят в следующем порядке:
1) выполняются все возможные склеивания 1-ого члена с остальными;
2) выполняются все возможные склеивания 2-ого члена с остальными, кроме 1-ого;
3) выполняются все возможные склеивания 3-ого члена с остальными, кроме 1-ого и второго и т.д.
Склеиваться могут только те члены, у которых число переменных с отрицаниями отличается на единицу. Результаты склеивания и поглощения:
Звездочками отмечают те члены СДНФ, которые поглощаются произведениями, образовавшимися после склеивания.
В рассматриваемом примере поглощаются все шесть исходных членов, поэтому СДНФ заданной функции имеет вид:
К этому выражению операции склеивания и поглощения применить нельзя, и, следовательно, оно является сокращенной дизъюнктивной нормальной формой логической функции, а его члены - простыми импликантами.
Похожие работы
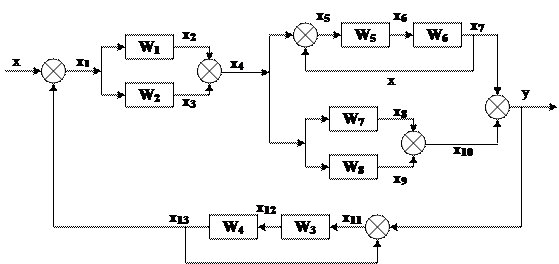
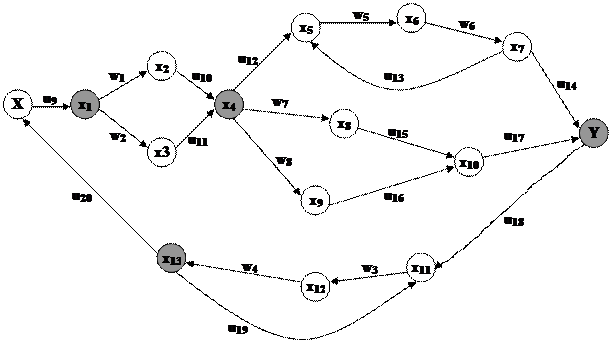
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
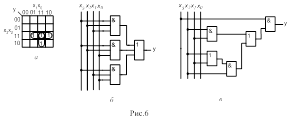
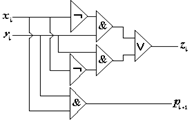
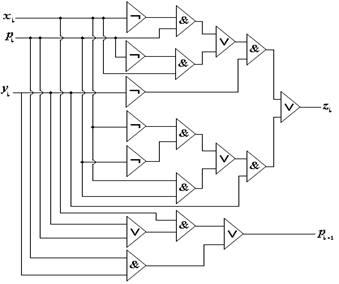
... порядка рис.7,б, которая хуже схемы рис.7,а по характеристикам быстродействия и сложности. Ухудшение характеристик оправдывается только возможностью реализации схемы на заданных стандартных элементах. 8. Комбинационные схемы Логическая схема (рис.8) с n входами и k выходами реализует систему переключательных функций y0 ...yk-1. Каждая функция yi(x0 ...xk-1) однозначно соответствует ...
... одно состояние из множества А, каждой строке – один входной сигнал из множества Z. На пересечении строки и столбца в таблице переходов, записывается состояние as, в которое должен перейти автомат из состояния am, под действием входного сигнала zf, т.е. as = σ(am, zf). На пересечении строки и столбца в таблице выходов записывается выходной сигнал wg, выдаваемый автоматом в состоянии am при ...
... к утверждению выводимости формулы Применение логики высказываний к анализу математических доказательств Ни у кого не возникает сомнения в том, что математические доказательства являются примерами строгих логических рассуждений. Аппарат логики высказываний позволяет нам прояснить структуру доказательств многих математических утверждений. Рассмотрим с точки зрения логики высказываний ...
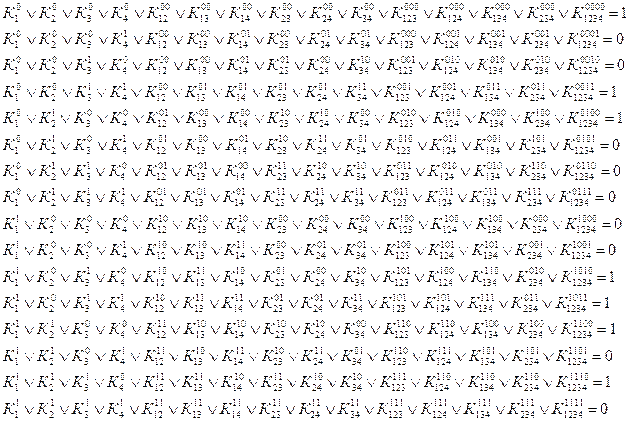
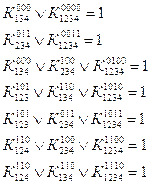
0 комментариев