Навигация
Примеры выполнения
3.2.2 Примеры выполнения
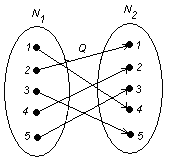
Пример 1: По заданной матрице смежности построить матрицу инцидентности.
implementation
procedure TForm1. UpDown1Click (Sender: TObject; Button: TUDBtnType);
begin
with UpDown1 do begin
with StringGrid1 do begin
RowCount:=Position;
ColCount:=Position;
end;
StringGrid2. RowCount:=Position;
end;
end;
procedure TForm1. BitBtn1Click (Sender: TObject);
var i, j, CD, P, n:byte;
MS:array of array of byte;
MI:array of array of ShortInt;
begin
P:=StrToInt (Edit1. Text);
SetLength (MS, P, P);
CD:=0;
for i:=0 to P‑1 do for j:=0 to P‑1 do begin
MS [i, j]:=StrToInt (StringGrid1. Cells [j, i]);
if MS [i, j]=1 then inc(CD);
end;
SetLength (MI, P, CD);
for i:=0 to High(MS) do for j:=0 to CD‑1 do MI [i, j]:=0;
n:=0;
for i:=0 to High(MS) do for j:=0 to High(MS) do
if MS [i, j]=1 then begin
MI [i, n]:=1;
MI [j, n]:=-1;
inc(n);
end;
StringGrid2. ColCount:=CD;
for i:=0 to High(MS) do for j:=0 to CD‑1 do
StringGrid2. Cells [j, i]:=IntToStr (MI[i, j]);
end;
end.
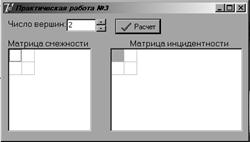
Рисунок 3.20 – Форма с результатом
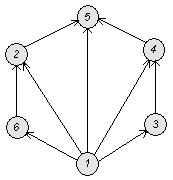
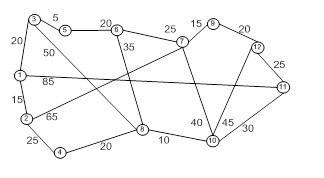
Пример 2: По заданной матрице смежности построить матрицу инцидентности.
var
Form1: TForm1;
const maxv=4;
type canh=record dinh1, dinh2:byte;
dodai:real; end;
dothi=record n:byte;
l:array [1..maxv, 1..maxv] of real;
x, y:set of 1..maxv;
t:array [1..maxv] of canh;
nt:byte;
it:real; end;
implementation
{$R *.dfm}
procedure TForm1. Button1Click (Sender: TObject);
var g:dothi;
min:real;
x, y, x0, y0:1..maxv;
i, j:byte;
begin memo1. Clear;
g.n:=maxv;
edit1. Text:=inttostr(maxv);
stringgrid1.cells [0,0]:=' Номер';
for i:=1 to maxv do begin
stringgrid1.cells [0, i]:=inttostr(i);
stringgrid1.cells [i, 0]:=inttostr(i); end;
g.nt:=0; g.it:=0; g.x:=[1..g.n]; g.y:=[1];
for i:=1 to maxv do
for j:=1 to maxv do g.l [i, j]:=strtofloat (stringgrid1. Cells [j, i]);
while g.nt<g.n‑1 do begin
min:=-1;
for x:=1 to g.n do
for y:=1 to g.n do
if (x in g.y) and (y in (g.x-g.y)) and (g.l [x, y]>0) then
begin
if (min=-1) or (min>g.l [x, y]) then begin
min:=g.l [x, y];
x0:=x; y0:=y; end;
end;
g.y:=g.y+[y0];
g.nt:=g.nt+1;
g.it:=g.it+min;
with g.t [g.nt] do begin
dinh1:=x0;
dinh2:=y0;
dodai:=min; end; end;
for i:=1 to (maxv‑1) do
with g.t[i] do
memo1. Lines.add ('Ребро: '+inttostr(dinh1)+inttostr(dinh2)+' '+
'Весом: '+floattostr(dodai));
end;
end.
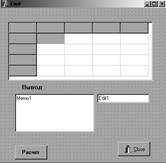
Рисунок 3.21 – Форма с результатом
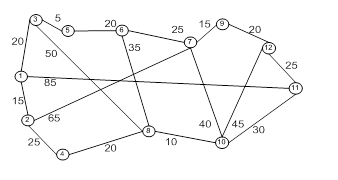
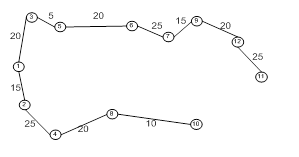
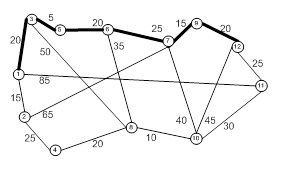
Пример 3: Составить приложение на Delphi, реалилующее алгоритм Уоршелла.
var
Form1: TForm1;
const maxv=4;
type canh=record dinh1, dinh2:byte;
dodai:real; end;
dothi=record n:byte;
l:array [1..maxv, 1..maxv] of real;
x, y:set of 1..maxv;
t:array [1..maxv] of canh;
nt:byte;
it:real; end;
implementation
{$R *.dfm}
procedure TForm1. Button1Click (Sender: TObject);
var g:dothi;
min:real;
x, y, x0, y0:1..maxv;
i, j:byte;
begin memo1. Clear;
g.n:=maxv;
stringgrid1.cells [0,0]:=' Номер';
for i:=1 to maxv do begin
stringgrid1.cells [0, i]:=inttostr(i);
stringgrid1.cells [i, 0]:=inttostr(i); end;
g.nt:=0; g.it:=0; g.x:=[1..g.n]; g.y:=[1];
for i:=1 to maxv do
for j:=1 to maxv do g.l [i, j]:=strtofloat (stringgrid1. Cells [j, i]);
while g.nt<g.n‑1 do begin
min:=-1;
for x:=1 to g.n do
for y:=1 to g.n do
if (x in g.y) and (y in (g.x-g.y)) and (g.l [x, y]>0) then
begin
if (min=-1) or (min>g.l [x, y]) then begin
min:=g.l [x, y];
x0:=x; y0:=y; end;
end;
g.y:=g.y+[y0];
g.nt:=g.nt+1;
g.it:=g.it+min;
with g.t [g.nt] do begin
dinh1:=x0;
dinh2:=y0;
dodai:=min; end; end;
for i:=1 to (maxv‑1) do
with g.t[i] do
memo1. Lines.add ('Ребро: '+inttostr(dinh1)+inttostr(dinh2)+' '+
'Весом: '+floattostr(dodai));
end;
end.
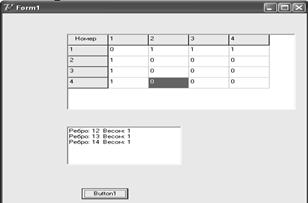
Рисунок 3.23 – Форма с результатом
Похожие работы
... Е и множество и мы рассматриваем все его подмножества, то множество Е называется униварсельным. Пример: Если за Е взять множество книг то его подмножества: художественные книги, книги по математике, физики, физики … Если универсальное множество состоит из n элементов, то число подмножеств = 2n. Если , состоящее из элементов E, не принадлежащих А, называется дополненным. Множество можно задать: ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
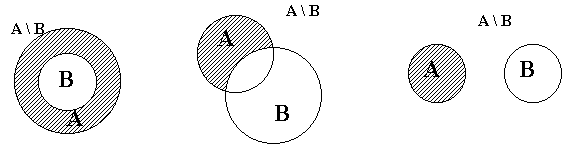
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
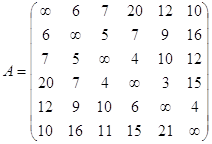
0 комментариев