Навигация
Алгоритмы генерации множеств
2.1.3 Алгоритмы генерации множеств
Реализация операций над подмножествами заданного универсума U
Пусть универсум U – конечный, и число элементов в нем не превосходит разрядности ЭВМ: мощность |U| < n. Элементы универсума нумеруются: U = {u1,…, un}. Подмножество А универсума U представляется кодом (машинным словом или битовой шкалой) С, в котором:

где С(i) – это i‑й разряд кода С.
Код пересечения множеств А и В есть поразрядное логическое произведение кода множества А и кода множества В. Код объединения множеств А и В есть поразрядная логическая сумма кода множества А и кода множества В. Код дополнения множества А есть инверсия кода множества А. В большинстве ЭВМ для этих операций есть соответствующие машинные команды. Таким образом, операции над небольшими множествами выполняются весьма эффективно.
Если мощность универсума превосходит размер машинного слова, но не очень велика, то для представления множеств используются массивы битовых шкал. В этом случае операции над множествами реализуются с помощью циклов по элементам массива [23].
Генерация всех подмножеств универсума
Во многих переборных алгоритмах требуется последовательно рассмотреть все подмножества заданного множества. В большинстве компьютеров целые числа представляются кодами в двоичной системе счисления, причем число 2k – 1 представляется кодом, содержащим k единиц. Таким образом, число 0 является представлением пустого множества 0, число 1 является представлением подмножества, состоящего из первого элемента, и т. д. Следующий тривиальный алгоритм перечисляет все подмножества n‑элементного множества (представлен в паскале-подобном коде, описание в [23]).
Алгоритм 1.1: Алгоритм генерации всех подмножеств n‑элементного множества
Вход: n ![]() 0 – мощность множества
0 – мощность множества
Выход: последовательность кодов подмножеств i
for i from 0 to 2n – 1 do
yield i
end for
Обоснование: Алгоритм выдает 2n различных целых чисел, следовательно, 2n различных кодов.
С увеличением числа n увеличивается количество двоичных разрядов, необходимых для его представления. Самое большое (из генерируемых) число 2n‑1 требует для своего представления ровно n разрядов. Таким образом, все подмножества генерируются, причем ровно по одному разу.
Во многих переборных задачах требуется рассмотреть все подмножества некоторого множества и найти среди них то, которое удовлетворяет заданному условию. При этом проверка условия часто может быть весьма трудоемкой и зависеть от состава элементов очередного рассматриваемого подмножества. В частности, если очередное рассматриваемое подмножество незначительно отличается по набору элементов от предыдущего, то иногда можно воспользоваться результатами оценки элементов, которые рассматривались на предыдущем шаге перебора. В таком случае, если перебирать множества в определенном порядке, можно значительно ускорить работу переборного алгоритма. [5]
Алгоритм построения бинарного кода Грея
Данный алгоритм генерирует последовательность всех подмножеств n‑элементного множества, причем каждое следующее подмножество получается из предыдущего удалением или добавлением одного элемента.
Алгоритм 1.2: Алгоритм построения бинарного кода Грея Вход: n![]() 0 – мощность множества
0 – мощность множества
Выход: последовательность кодов подмножеств В
В: array [l..n] of 0..1 {битовая шкала для представления подмножеств}
for i from 1 to n do
B[i]: = 0 {инициализация} end for
yield В {пустое множество}
for i from I to 2n – 1 do
p: = Q(i) {определение элемента, подлежащего добавлению или удалению}
B[р]: = 1 – В[р] {добавление или удаление элемента}
yield В {очередное подмножество} end for
proc Q(i) {количество 2 в разложении i на множители + 1} q: = l; j: = i while j четно do
j:=j/2; q: = q + l end while return q end proc
Обоснование
Для n = 1 искомая последовательность кодов суть 0,1. Пусть есть искомая последовательность кодов В1,…, ![]() для n = к. Тогда последовательность кодов B10,…,
для n = к. Тогда последовательность кодов B10,…, ![]() 0,
0, ![]() 1, …. B11 будет искомой последовательностью для n = к + 1. Действительно, в последовательности B10,…,
1, …. B11 будет искомой последовательностью для n = к + 1. Действительно, в последовательности B10,…, ![]() 0,
0, ![]() 1,…, В11 имеется 2k+1 кодов, они все различны и соседние различаются ровно в одном разряде по строению. Именно такое построение и осуществляет данный алгоритм. На нулевом шаге алгоритм выдает правильное подмножество В (пустое). Пусть за первые 2k – 1 шагов алгоритм выдал последовательность значений В. При этом В [k + 1] = В [k + 2] = • • • = В[n] = 0. На 2 k‑ом шаге разряд В [k + 1] изменяет свое значение с 0 на 1. После этого будет повторена последовательность изменений значений В [1. k] в обратном порядке, поскольку Q (2k + m) = Q (2k – m) для
1,…, В11 имеется 2k+1 кодов, они все различны и соседние различаются ровно в одном разряде по строению. Именно такое построение и осуществляет данный алгоритм. На нулевом шаге алгоритм выдает правильное подмножество В (пустое). Пусть за первые 2k – 1 шагов алгоритм выдал последовательность значений В. При этом В [k + 1] = В [k + 2] = • • • = В[n] = 0. На 2 k‑ом шаге разряд В [k + 1] изменяет свое значение с 0 на 1. После этого будет повторена последовательность изменений значений В [1. k] в обратном порядке, поскольку Q (2k + m) = Q (2k – m) для ![]()
Пример 2.4
Таблица 2.5 – Протокол выполнения алгоритма 1.2 для п = 3
| i | Р | В | ||
| 0 | 0 | 0 | ||
| 1 | 1 | 0 | 0 | 1 |
| 2 | 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 | 0 |
| 4 | 3 | 1 | 1 | 0 |
| 5 | 1 | 1 | 1 | 1 |
| 6 | 2 | 1 | 0 | 1 |
| 7 | 1 | 1 | 0 | 0 |
Представление множеств упорядоченными списками
Если универсум очень велик (или бесконечен), а рассматриваемые подмножества универсума не очень велики, то представление с помощью битовых шкал не является эффективным с точки зрения экономии памяти. В этом случае множества обычно представляются списками элементов. Элемент списка при этом представляется записью с двумя полями: информационным и указателем на следующий элемент. Весь список представляется указателем на первый элемент.
elem = record
i: info; {информационное поле}
n: elem {указатель на следующий элемент} end record
При таком представлении трудоемкость операции ![]() составит O(n), а трудоемкость операций
составит O(n), а трудоемкость операций ![]() составит О(nm), где n и m – мощности участвующих в операции множеств.
составит О(nm), где n и m – мощности участвующих в операции множеств.
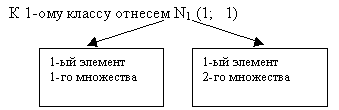
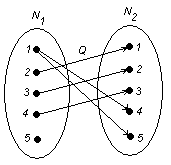
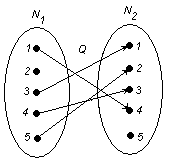
Если элементы в списках упорядочить, например, по возрастанию значения поля i, то трудоемкость всех операций составит О(n). Эффективная реализация операций над множествами, представленными в виде упорядоченных списков, основана на весьма общем алгоритме, известном как алгоритм типа слияния.
1
1 1
1 2 1
13 3 1
14 6 4 1
Рисунок 2.9 – Иллюстрация к алгоритму слияния
В этом равнобедренном треугольнике каждое число (кроме единиц на боковых сторонах) является суммой двух чисел, стоящих над ним. Число сочетаний С (m, n) находится в (m + 1) – м ряду на (n + 1) – м месте.
Генерация подмножеств
Элементы множества {1,…, m} упорядочены. Поэтому каждое n‑элементное подмножество также можно рассматривать как упорядоченную последовательность. На множестве таких последовательностей естественным образом определяется лексикографический порядок. Следующий простой алгоритм генерирует все n‑элементные подмножества m‑элементного множества в лексикографическом порядке.
Алгоритм 1.3. Генерация n‑элементных подмножеств m‑элементного множества
Вход: n – мощность подмножества, m – мощность множества, m![]() n > 0.
n > 0.
Выход: последовательность всех n‑элементных подмножеств m‑элементного множества в лексикографическом порядке.
for i from 1 to m do
A[i]: = i {инициализация исходного множества} end for
if m = n then
yield A [1..n] {единственное подмножество} exit end if
p: = n {p – номер первого изменяемого элемента} while p ![]() 1 do
1 do
yield A [1..n] {очередное подмножество в первых n элементах массива А} if А[i] = m then
р: = р – 1 {нельзя увеличить последний элемент} else
р:=n {можно увеличить последний элемент} end if if p
Похожие работы
... Е и множество и мы рассматриваем все его подмножества, то множество Е называется униварсельным. Пример: Если за Е взять множество книг то его подмножества: художественные книги, книги по математике, физики, физики … Если универсальное множество состоит из n элементов, то число подмножеств = 2n. Если , состоящее из элементов E, не принадлежащих А, называется дополненным. Множество можно задать: ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
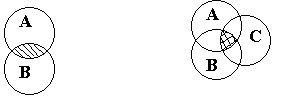
0 комментариев