Теоретическая часть
Методы, используемые при поиске и сортировке
Оценки времени исполнения
Приложение на Delphi, в котором представлена работа некоторых методов сортировки и поиска
Пример выполнения
Вопросы для самопроверки
Представление множеств и отношений в программах
Алгоритмы генерации множеств
Then
Варианты заданий
Теоретическая часть
Примеры выполнения
Вариантв заданий
Перевод даты рождения в двоичную систему
Вопросы для самопроверки
Вопросы для самопроверки
Процедура основного обработчика
Вопросы для самопроверки
Практическая часть
Дешифраторы
Навигация
Вопросы для самопроверки
Основы дискретной математики
179431
знак
27
таблиц
82
изображения
4.4 Вопросы для самопроверки
1) Чем отличается кортеж от обычного множества?
2) Приведите пример использования кортежей в программировании.
3. Какие операции над множествами Вы знаете?
4) Какой способ существует для графического изображения множеств?
5) Приведите пример универсального множества, которое используется в данной практической работе.
6) Какие операции (логические связки) из алгебры логики Вы знаете?
7) Возможно ли провести аналогию между операциями над множествами и логическими операциями?
8) Какое правило используется при построении СДНФ логической функции?
9) Какое правило используется при построении СКНФ логической функции?
10) Каков алгоритм перевода числа из десятичной системы счисления в двоичную систему счисления?
11) Почему логические функции и логические переменные часто называют двоичными?
12) Какая связь существует между логическими функциями и функционированием компьютера, отдельных его устройств?
Практическая работа № 5. Исследование логических функций
Цель работы: изучение существующих форм представления логических функций. Построение совершенных нормальных форм логических функций. Построение таблиц истинности и арифметических моделей логических функций в приложениях на Delphi.
Примечание: все теоретические сведения, необходимые для выполнения данной работы, содержатся в [25], в лекциях и в материалах семинарских занятий.
5.1 Задание к работе
1. Используя средства Excel и Delphi, построить таблицы истинности заданных логических функций, если требуется, то предварительно упростить выражения, используя законы алгебры логики и следствия из них.
2. Используя средства Excel и Delphi, построить арифметические модели заданных логических функций.
3. Представить заданные логические функции в виде СДНФ, СКНФ и СПНФ.
4. Построить логические функциональные схемы для заданных логических функций F1 и F2.
5. Сделать выводы.
5.2 Практическая часть
5.2.1 Пример выполнения
Задание: Построить таблицу истинности, СДНФ, СКНФ, СПНФ и логические функциональные схемы для данных логических функций:
F1=
F2=
Код программы построения таблицы истинности логический функций:
Procedure TForml. ButtonlClick (Sender: TObject);
var xl, x2, x3:boolean; i:byte;
a1, a2, a3: string;
begin
Stringgridl. Cells [l, 0]:='xl';
Stringgridl. Cells [2,0]:='x2';
Stringgridl. Cells [3,0]:='x3';
Stringgrid1. Cells [4,0]:=F1';
Stringgridl. Cells [5,0]:='F2';
for i:=l to 8 do begin Stringgrid1. Cells [0, i]:=inttostr (i‑1);
if i<=4 then Stringgridl. Cells [l, i]:=’0’ else Stringgridl. Cells [l, i]:=1;
if (i<=2) or (i=5) or (i=6) then Stringgridl. Cells [2, i]:='0’ else Stringgridl. Cells [2, i]:=' 1';
if (i mod 2 >0) then Stringgridl. Cells [3, i]:='0' else Stringgridl. Cells [3, i]:=1; end;
for i:=l to 8 do begin
x1:=strtobool (Stringgrid 1. Cells [1, i]);
x2:=strtobool (Stringgridl. Cells [2, i]);
x3:=strtobool (Stringgridl. Cells [3, i]);
if (x2 and x3) or (not(xl) and not(x2)) or (x3 and not(xl)) then
Stringgridl. Cells [4, i]:=’1’ else Stringgridl. Cells [4, i]:='0';
if (x2 and x3) or (not(xl) and not(x2) and not(x3)) then Stringgridl. Cells [5, i]:=1 else Stringgridl. Cells [5, i]:='0'; end; end;
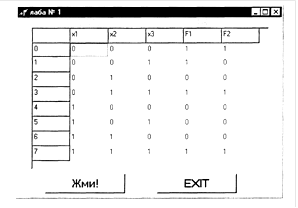
Рисунок 5.1 – Форма с результатами
МДНФ:
F1 = 
F2 = 
МКНФ:
F1 = 
F2 = 
СПНФ:
F1 =
F2 =
|
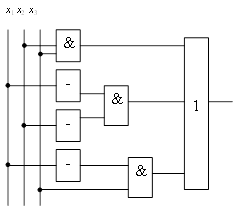
| Рисунок 5.2 – Логическая схема для МКНФ функции F1 |
5.2.2 Варианты заданий
1) Заданы логические функции: F1= 1 на наборах 0, 3 и 
2) Заданы логические функции: F1= 1 на наборах 0, 1, 3 и 
3) Заданы логические функции: F1= 1 на наборах 3, 7 и 
4) Заданы логические функции: F1= 1 на наборах 0, 1, 3, 7 и 
5) Заданы логические функции: F1= 1 на наборах 0,1,2,3,7 и 
6) Заданы логические функции: F1= 1 на наборах 2,5,6 и 
7) Заданы логические функции: F1= 1 на наборах 0, 2,5,7 и 
8) Заданы логические функции: F1= 1 на наборах 0, 1,3 и 
9) Заданы логические функции: F1= 1 на наборах 3,4,6,7 и 
10) Заданы логические функции: 
и 
11) Заданы логические функции: 
и 
12) Заданы логические функции: 
и 
13) Заданы логические функции: 
и 
14) Заданы логические функции: 
и 
15) Заданы логические функции: 
и 
16) Заданы логические функции: 
и 
17) Заданы логические функции: 
и 
18) Заданы логические функции: 
и 
19) Заданы логические функции: 
и 
20) Заданы логические функции: 
и 
21) Заданы логические функции: и
22) 
23) Заданы логические функции: 
и 
24) Заданы логические функции: и 
25) Заданы логические функции: 
и 
26) Заданы логические функции: и 
27) Заданы логические функции: и 
28) Заданы логические функции: 
и 
29) Заданы логические функции: и 
30) Заданы логические функции: и 
31) Заданы логические функции: и 
32) Заданы логические функции: F1=1 на наборах 4,5,7 и 
33) Заданы логические функции: F1=0 на наборах 2,4 и 
34) Заданы логические функции: 
и 
35) Заданы логические функции: 
и 
36) Заданы логические функции: 
и 
37) Заданы логические функции: 
и 
Похожие работы
... Е и множество и мы рассматриваем все его подмножества, то множество Е называется униварсельным. Пример: Если за Е взять множество книг то его подмножества: художественные книги, книги по математике, физики, физики … Если универсальное множество состоит из n элементов, то число подмножеств = 2n. Если , состоящее из элементов E, не принадлежащих А, называется дополненным. Множество можно задать: ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
0 комментариев