Навигация
Проверочный расчёт зубьев колёс на контактную прочность
4.2.1 Проверочный расчёт зубьев колёс на контактную прочность
После определения геометрических размеров рабочие поверхности зубьев необходимо проверить на контактную прочность. Для этого следует определить рабочие контактное напряжение σн и сравнить с допускаемым σнр. Должно выполняться условие: σн ≤ σнр.
Рабочее контактное напряжение, МПа:
σн = ZЕ. ZH. Zε.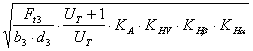 ; (4.25)
; (4.25)
где: ZЕ = 190 – коэффициент, учитывающий механические свойства материалов сопряжённых зубчатых колёс, изготовленных из стали.
ZH – коэффициент, учитывающий форму сопряжённых поверхностей зубьев в полюсе зацепления.
ZH = 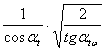 ; (4.26)
; (4.26)
где: αt – делительный угол профиля в торцовом сечении, град.
αtω – угол зацепления, град.
для прямозубых передач без смещения: αt = αtω = 200.
ZH =  = 2,495; (4.27)
= 2,495; (4.27)
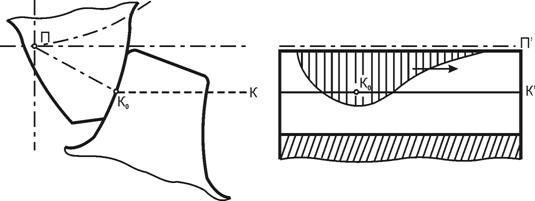
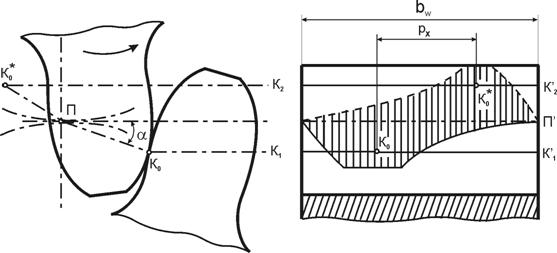
Zε – коэффициент, учитывающий суммарную длину контактных линий прямозубой передачи:
Zε = ![]() ; (4.28)
; (4.28)
где: εα – коэффициент торцового перекрытия;
εα = [1.88 - 3.22 . (![]() )]; (4.29)
)]; (4.29)
εα = 1.88 - 3.22. (![]() ) = 1.739;
) = 1.739;
Zε = ![]() = 0,868,
= 0,868,
Ft3 – окружная сила на делительном диаметре, Н:
Ft3 = ![]() ; (4.30)
; (4.30)
Ft3 = ![]() = 3743,9 Н.
= 3743,9 Н.
КА = 1,1 – коэффициент внешней динамической нагрузки при равномерном нагружении двигателя и ведомой машины.
КHV – коэффициент, учитывающий динамическую нагрузку.
КHV = 1 + ![]() ; (4.31)
; (4.31)
где: ωнv – удельная окружная динамическая сила, Н/мм:
ωнv = δн. q0. V2.![]() ; (4.32)
; (4.32)
где: δн = 0,06 – коэффициент, учитывающий влияние вида зубчатой передачи.
q0 = 5,6 при m ≤ 3.55 – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса 8-й степени точности:
ωнv = 0.06 . 5,6 . 1.404 .![]() = 4,24 Н/мм;
= 4,24 Н/мм;
КHV = 1 + ![]() = 1,084.
= 1,084.
Кнβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:
Кнβ = 1 + (![]() ) . Кнω; (4.33)
) . Кнω; (4.33)
где: К0нβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи:
К0нβ = 1,1
Кнα = 1 – коэффициент, учитывающий распределение нагрузки между зубьями прямозубых передач,
Кнω – коэффициент, учитывающий приработку зубьев;
Кнω = 1 - ![]() ; (4.34)
; (4.34)
Кнω = 1 - ![]() = 0,217;
= 0,217;
Найдя все необходимые коэффициенты, найдём рабочее контактное напряжение, МПа:
σн = 190 . 2,495 . 0,868 .![]() = 344,36 МПа;
= 344,36 МПа;
Проверка выполнения условия: σн ≤ σнр;
344,45 < 373,1.
Вывод: условие выполнено, верно.
Похожие работы
... вращения и угловых скоростей валов привода. n=1450 мин-1; c-1, Вал II: мин-1; c-1, Вал III: мин-1; c-1, Вал IV: мин-1; c-1. Определение вращающих моментов на валах привода. Н∙м; Вал II: Н∙м; Вал III: Н∙м; Вал IV: Н∙м. 2 ВЫБОР МАТЕРИАЛА И ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ Выбираю материалы со средними механическими ...
дрические, конические, коническо-цилиндрические), относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные), особенностями кинематической схемы (развернутая, соосная, с раздвоенной ступенью). Возможности получения больших передаточных чисел при малых габаритах обеспечивают планетарные и волновые редукторы. Сборку редуктора производят в соответствии со сборочным ...
... . , диаметр под подшипник принимаем . , где . , диаметр буртика под подшипник принимаем: 6. Эскизная компоновка редуктора. 6.1 исходные данные: , , . 6.2 Построение схемы эскизной компоновки редуктора, и расчет всех размеров. , принимаем: . . 7.Выбор подшипников качения. 7.1 Исходные данные: Быстроходный вал: , , . Промежуточный ...
... a2= m(z1+z2)/2= 0,3(24+49)/2= 10,95 a3= m(z1+z2)/2= 0,3(24+54)/2= 11,7 a4= m(z1+z2)/2= 0,3(24+55)/2= 11,85 a5= m(z1+z2)/2= 0,3(24+68)/2= 13,8 Определим ширину венца: b= (3…15)m= 10·0,3= 3 Определим высоту зуба: h= 2,5m= 2,5·0,3= 0,75 5. Разработка конструкций редуктора Разработка конструкции состоит в расчете и выборе его элементов: зубчатые колеса, валы, подшипники и корпуса. ...

0 комментариев