Определение геометрических и кинематических параметров быстроходной ступени редуктора (колёса косозубые)

4.3. Определение геометрических и кинематических параметров быстроходной ступени редуктора (колёса косозубые)

Межосевое расстояние быстроходной ступени, мм:

а_ωб = а_ωт;

а_ωб =196 мм;

Модуль зацепления, мм:

m = (0,01 ÷ 0,02) ^. а_ωб; (4.56)

m = 0,015 ^. 196 = 3,16 мм.

Полученное значение округляем до стандартного: m = 3,5 мм.

Число зубьев:

шестерни:

Z₁ = ; (4.57)

Где – угол наклона зубьев β косозубых зубчатых колёс выбирается из условия получения коэффициента торцового перекрытия ε_α более 1,1, которому соответствуют значения β = (8 ÷ 18)⁰. При расчёте передачи первоначально принимается любое значение угла β из указанного интервала.

Число зубьев шестерни быстроходной ступени должно находиться в интервале Z₁ = (22 ÷ 35) зубьев.

Z₁ =  = 29,24;

округляем до целого числа: Z₁ = 29;

колеса:

Z₂ = U_Б^. Z₁; (4.58)

Z₂ = 2.7 ^. 29 = 78,3;

округляем до целого числа: Z₂ = 79.

Уточнённое значение угла наклона зубьев, град:

cos β = ; (4.59)

cos β =  = 0.964, β = 15⁰22´;

Делительные диаметры, мм:

шестерни:

d₁ = ; (4.60)

d₁ =  = 105,2 мм;

колеса:

d = ; (4.61)

d₂ =  = 286,8 мм;

Диаметры вершин зубьев, мм;

шестерни:

d_а1 = d₁ + 2 ^. m; (4.62)

d_а1 = 105,2 + 2 ^. 3,5 = 112,2 мм;

колеса:

d_а2 = d₂ + 2 ^. m; (4.63)

d_а2 = 286,8 + 2 ^. 3,5 = 293,8 мм;

Диаметры впадин зубьев, мм;

шестерни:

d_f1 = d₁ – 2,5 ^. m; (4.64)

d_f1 = 105,2 – 2,5 ^. 3,5 = 99,55 мм;

колеса:

d_f2 = d₂ – 2,5 ^. m; (4.65)

d_f2 = 286,8 – 2,5 ^. 3,5 = 278,05 мм;

Рабочая ширина зубчатого венца, мм;

колеса:

b₂ = ψ_ba^. а_ωБ; (4.66)

b₂ = 0,4 ^. 196 = 78,4 мм;

Округляем до целого числа – b₂ = 78 мм.

шестерни:

b₁ = b₂ + m; (4.67)

b₁ = 78,4 + 3,5 = 81,9 мм;

Округляем до целого числа – b₁ = 82 мм.

Окружная скорость зубчатых колёс, м/с:

V₁ = ; (4.68)

V₁ =  = 3,56 м/с;

4.3.1. Проверочный расчёт зубьев колёс на контактную прочность

Рабочие контактное напряжение, МПа;

σ_н = Z_E^. Z_H^. Z_ε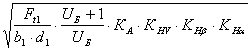^.; (4.69)

где: Z_E = 190 – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колёс, изготовленных из стали;

Z_H – коэффициент, учитывающий форму сопряжённых поверхностей зубьев в полюсе зацепления;

Z_H = 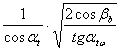; (4.70)

где: α_t – делительный угол профиля в торцовом сечении, град;

α_t = arctg ; (4.71)

α_t = arctg  = 20.68⁰;

α_tω – угол зацепления, град;

для передач без смещения α_tω = α_t;

β_b – основной угол наклона, град;

β_b = arcsin(sin β ^. cos 20⁰); (4.72)

β_b = arcsin(sin 15º22´ ^. cos 20⁰) = 14,4⁰; (4.73)

Z_H = 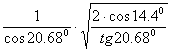 = 2.42;

Z_ε – коэффициент, учитывающий суммарную длину контактных линий косозубой передачи;

Z_ε = ; (4.74)

где: ε_α – коэффициент торцового перекрытия для передач без смещения, при β < 20⁰;

ε_α = 1,88 - 3,22 ^. () ^. cos β; (4.75)

ε_α = 1,88 - 3,22^. () ^. cos 15⁰22´= 1,67;

Z_ε =  = 0,775;

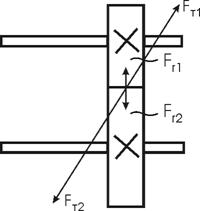
F_t1 – окружная сила на делительном диаметре, Н;

F_t1 = ; (4.76)

F_t1 =  = 1568 Н;

К_А = 1.1 – смотреть п. 4.2.1.

К_HV – коэффициент, учитывающий динамическую нагрузку;

К_HV = 1 + ; (4.77)

где: ω_HV – удельная окружная динамическая сила, Н/мм;

ω_HV = δ_Н^. q₀^. V₁^.; (4.78)

где: δ_Н = 0,02 – коэффициент, учитывающий влияние вида зубчатой передачи;

q₀ = 5,6 – смотреть п. 4.2.1.

ω_HV = 0.02 ^. 5,6 ^. 3,56 ^. = 3,397;

К_HV = 1 +  = 1,162;

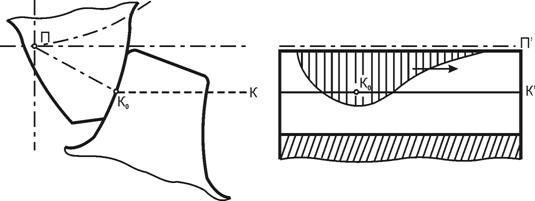
К_Hβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;

К_Hβ = 1 + (K⁰_Hβ– 1) ^. К_Hω; (4.79)

где: K⁰_Hβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи;

K⁰_Hβ = 1,1

К_Hω – коэффициент, учитывающий приработку зубьев;

К_Hω = 1 – ; (4.80)

К_Hω = 1 –  = 0.32;

К_Hβ = 1 + (1.1– 1) ^. 0.32 = 1.032;

К_Hα – коэффициент, учитывающий распределение нагрузки между зубьями;

К_Hα = 0,9 + 0,4 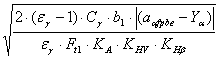^.; (4.81)

где: ε_γ – суммарный коэффициент перекрытия;

ε_γ= ε_α + ε_β; (4.82)

ε_α – коэффициент торцового перекрытия;

ε_α= ε_α1 + ε_α2; (4.83)

где:

ε_α1 = ; (4.84)

ε_α2 = ; (4.85)

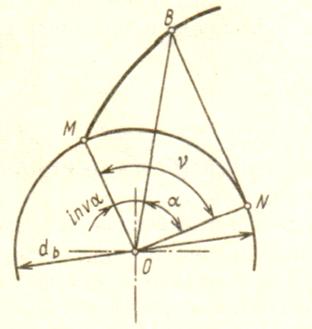
где: α_α1, α_α2 – углы профиля зуба в точках на окружностях вершин, град;

α_α1 = arcos ; (4.86)

α_α2 = arcos ; (4.87)

где: d_b1, d_b2 – основные диаметры шестерни и колеса, мм;

d_b1 = d₁^. cos α_t; (4.88)

d_b1 = 105,3 ^. cos 20.68⁰ = 98,5 мм;

d_b2 = d₂^. cos α_t; (4.89)

d_b2 = 268,8 ^. cos 20.68⁰ = 283,3 мм;

α_α1 = arcos  = 28,68⁰;

α_α2 = arcos  = 24,04⁰;

ε_α1 =  = 0,784;

ε_α2 =  = 0,868;

ε_α= 0,784 + 0,868 = 1,65;

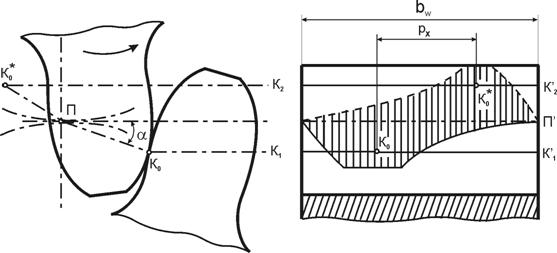
ε_β – коэффициент осевого перекрытия;

ε_β = ; (4.90)

где: P_X – осевой шаг, мм;

P_X = ; (4.91)

P_X =  = 41,49 мм;

ε_β =  = 1,976;

ε_γ= 1,65 + 1,976 = 3,626;

К_Hα = 1,05;

Найдя все необходимые коэффициенты и подставив их в формулу рабочего контактного напряжения, найдем σ_Н:

σ_н = 190 ^. 2,42 ^. 0,775 ^. = 209,2 МПа.

Похожие работы

Проектирование индивидуального привода

Скачать

20648

4

3

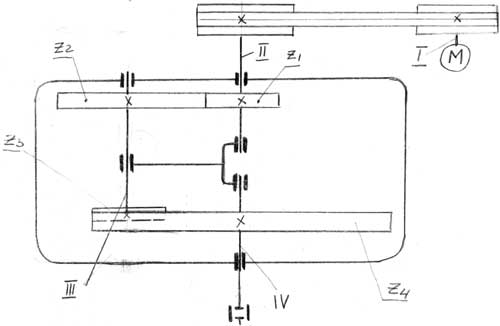
... вращения и угловых скоростей валов привода. n=1450 мин-1;  c-1, Вал II:  мин-1;  c-1, Вал III:  мин-1;  c-1, Вал IV:  мин-1;  c-1. Определение вращающих моментов на валах привода. Н∙м; Вал II: Н∙м; Вал III: Н∙м; Вал IV: Н∙м. 2 ВЫБОР МАТЕРИАЛА И ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ Выбираю материалы со средними механическими ...

Проектирование механической системы промышленного робота манипулятора

Скачать

12708

2

8

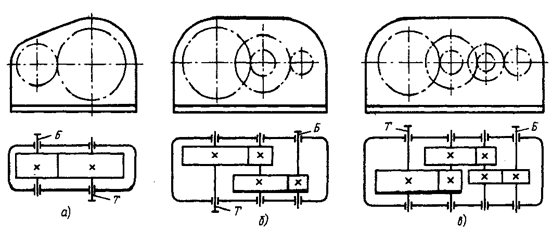
дрические, конические, коническо-цилиндрические), относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные), особенностями кинематической схемы (развернутая, соосная, с раздвоенной ступенью). Возможности получения больших передаточных чисел при малых габаритах обеспечивают планетарные и волновые редукторы. Сборку редуктора производят в соответствии со сборочным ...

Расчет редуктора

Скачать

15698

1

41

... . , диаметр под подшипник принимаем . , где . , диаметр буртика под подшипник принимаем: 6. Эскизная компоновка редуктора.   6.1 исходные данные: , , .   6.2 Построение схемы эскизной компоновки редуктора, и расчет всех размеров. , принимаем: . . 7.Выбор подшипников качения.   7.1 Исходные данные: Быстроходный вал: , , . Промежуточный ...

Расчет редуктора точного прибора

Скачать

43940

3

5

... a2= m(z1+z2)/2= 0,3(24+49)/2= 10,95 a3= m(z1+z2)/2= 0,3(24+54)/2= 11,7 a4= m(z1+z2)/2= 0,3(24+55)/2= 11,85 a5= m(z1+z2)/2= 0,3(24+68)/2= 13,8 Определим ширину венца: b= (3…15)m= 10·0,3= 3 Определим высоту зуба: h= 2,5m= 2,5·0,3= 0,75 5. Разработка конструкций редуктора Разработка конструкции состоит в расчете и выборе его элементов: зубчатые колеса, валы, подшипники и корпуса. ...