Расчёт зубьев на прочность при изгибе

4.2.2 Расчёт зубьев на прочность при изгибе

Выносливость зубьев, для предотвращения усталостного излома, для каждого колеса сопоставлением расчетного местного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения:

σ_F ≤ σ_FP;

Расчётное местное напряжение при изгибе:

для шестерни –

σ_F3 = ; (4.35)

для колеса –

σ_F4 = σ_F3^.; (4.36)

где: К_F – коэффициент нагрузки.

К_F = К_А^. К_FV^. K_Fβ^. K_Fα; (4.37)

где: К_FV – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса.

К_FV = 1 + ; (4.38)

где: ω_FV – удельная окружная динамическая сила, Н/мм:

ω_FV = δ_F^. q₀^. V₂^.; (4.39)

где: δ_F = 0.16 – коэффициент, учитывающий влияние вида зубчатой передачи,

q₀ = 5,6 при m ≤ 3.55 – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса 8-й степени точности:

ω_FV = 0,16 ^. 5,6 ^. 1,404 ^. = 11,32 Н/мм;

К_FV = 1 +  = 1,225.

K_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий,

K_Fβ = ; (4.40)

где:

N_F = ; (4.41)

где: h – для прямозубого зацепления:

h = ; (4.42)

h =  = 4,025;

N_F = 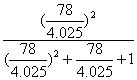 = 0,949;

K_Fβ =  = 1,095;

K_Fα = K_нα = 1 – коэффициент, учитывающий распределение нагрузки между зубьями:

К_F = 1,1 ^. 1,225 ^. 1,095 ^. 1 = 1,476;

Y_FS3, Y_FS4 – коэффициенты, учитывающие форму зуба и концентрацию напряжений, определяемые для шестерни и колеса в зависимости от числа зубьев Z₃ и Z₄ по графику зависимости (рис. 4.2).

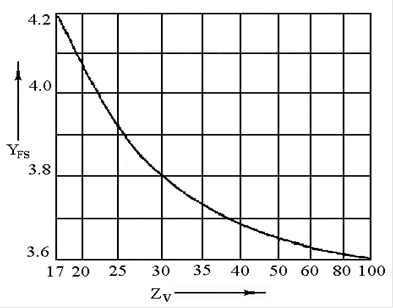
рис. 4.2

Y_β = 1 – коэффициент, учитывающий наклон зуба прямозубых передач;

Y_ε = 1 – коэффициент, учитывающий перекрытие зубьев:

Найдя все необходимые коэффициенты, найдём расчётное местное напряжение при изгибе для шестерни и колеса, МПа:

для шестерни:

σ_F3 =  = 72,78 МПа;

для колеса:

σ_F4 = 72,78 ^. = 69,51 МПа.

Допускаемое напряжение, МПа:

σ_FP = ; (4.43)

где: σ_Flimb – предел выносливости зубьев при изгибе, МПа:

σ_Flimb = ; (4.44)

где: σ⁰_Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа:

σ⁰_Flimb = 1,75 ^. НВ; (4.45)

Y_T = 1 – коэффициент, учитывающий технологию изготовления зубчатых колёс;

Y_Z = 1 – коэффициент, учитывающий способ получения заготовки зубчатого колеса (ковка или штамповка);

Y_q = 1 – коэффициент, учитывающий отсутствие шлифовки переходной поверхности зубьев;

Y_d = 1 – коэффициент, учитывающий отсутствие деформационного упрочнения или электрохимической обработки переходной поверхности;

Y_A = 1 – коэффициент, учитывающий влияние характера приложения нагрузки (односторонняя):

для шестерни:

σ⁰_Flimb3 = 1,75 ^. НВ₃; (4.46)

σ⁰_Flimb3 = 1,75 ^. 269 = 470,75 МПа;

σ_Flimb3 =  = 470,75 Мпа;

для колеса:

σ⁰_Flimb4 = 1,75 ^. НВ₄; (4.47)

σ⁰_Flimb4 = 1,75 ^. 220 = 385 МПа;

σ_Flimb4 =  = 385 МПа.

Y_N – коэффициент долговечности:

для шестерни:

Y_N3 = 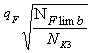 ≤ 4 (4.48)

для колеса:

Y_N4 = 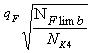 ≤ 4 (4.49)

где N_Flimb= 4·10⁶ – базовое число циклов напряжений;

N_К – суммарное число циклов напряжений, определяемое для шестерни и колеса, миллионов циклов,

для шестерни:

N_K3 = 60 · n₂ · L_h; (4.50)

N_K3 = 60 · 239,5 · 20000 = 287400000,

для колеса:

N_K4 = 60 · n₃ · L_h; (4.51)

N_K4 = 60 · 98.2 · 20000 = 117840000,

где: n₂, n₃ – частоты вращения шестерни и колеса тихоходной ступени, об/мин.

Так как, N_K3 > N_Flimb и N_K4 > N_Flimb, то поэтому принимаем Y_N = 1.

q_F = 6 – показатель степени для зубчатых колёс с однородной структурой материала;

Y_δ – коэффициент, учитывающий чувствительность материала к концентрации напряжений;

Y_δ = 1,082 – 0,172 ^. lg m; (4.52)

Y_δ = 1,082 – 0,172 ^. lg 3,5 = 0,989;

Y_R = 1,2 – коэффициент, учитывающий шероховатость переходной поверхности (при нормализации или улучшении);

Y_Х – коэффициент, учитывающий размеры зубчатого колеса;

Y_Х = 1,05 – 0,000125 ^. d_i; (4.53)

где: d_i – диаметр делительной окружности зубчатого колеса тихоходной ступени, мм:

для шестерни:

Y_Х3 = 1,05 – 0,000125 ^. 112 = 1,0336;

для колеса:

Y_Х4 = 1,05 – 0,000125 ^. 280 = 1,015;

S_F = 1,7 – коэффициент запаса прочности, для углеродистой и легированной сталей, подвергнутых нормализации или улучшению.

Допускаемое напряжение, МПа:

для шестерни:

σ_FP3 = ; (4.54)

σ_FP3 =  = 340,5 МПа;

для колеса:

σ_FP4 = ; (4.55)

σ_FP4 =  = 272,8 МПа;

Получив все необходимые напряжения, проверим выносливость зубьев, необходимую для предотвращения усталостного излома.

для шестерни:

σ_F3 ≤ σ_FP3;

72,8 < 340,5;

для колеса:

σ_F4 ≤ σ_FP4;

69,51 < 272,8.

Полученные неравенства верны, значит, расчёты выполнены верно.

Похожие работы

Проектирование индивидуального привода

Скачать

20648

4

3

... вращения и угловых скоростей валов привода. n=1450 мин-1;  c-1, Вал II:  мин-1;  c-1, Вал III:  мин-1;  c-1, Вал IV:  мин-1;  c-1. Определение вращающих моментов на валах привода. Н∙м; Вал II: Н∙м; Вал III: Н∙м; Вал IV: Н∙м. 2 ВЫБОР МАТЕРИАЛА И ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ Выбираю материалы со средними механическими ...

Проектирование механической системы промышленного робота манипулятора

Скачать

12708

2

8

дрические, конические, коническо-цилиндрические), относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные), особенностями кинематической схемы (развернутая, соосная, с раздвоенной ступенью). Возможности получения больших передаточных чисел при малых габаритах обеспечивают планетарные и волновые редукторы. Сборку редуктора производят в соответствии со сборочным ...

Расчет редуктора

Скачать

15698

1

41

... . , диаметр под подшипник принимаем . , где . , диаметр буртика под подшипник принимаем: 6. Эскизная компоновка редуктора.   6.1 исходные данные: , , .   6.2 Построение схемы эскизной компоновки редуктора, и расчет всех размеров. , принимаем: . . 7.Выбор подшипников качения.   7.1 Исходные данные: Быстроходный вал: , , . Промежуточный ...

Расчет редуктора точного прибора

Скачать

43940

3

5

... a2= m(z1+z2)/2= 0,3(24+49)/2= 10,95 a3= m(z1+z2)/2= 0,3(24+54)/2= 11,7 a4= m(z1+z2)/2= 0,3(24+55)/2= 11,85 a5= m(z1+z2)/2= 0,3(24+68)/2= 13,8 Определим ширину венца: b= (3…15)m= 10·0,3= 3 Определим высоту зуба: h= 2,5m= 2,5·0,3= 0,75 5. Разработка конструкций редуктора Разработка конструкции состоит в расчете и выборе его элементов: зубчатые колеса, валы, подшипники и корпуса. ...