Навигация
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ. КАЧЕСТВО ПРОЦЕССА УПРАВЛЕНИЯ
6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ. КАЧЕСТВО ПРОЦЕССА УПРАВЛЕНИЯ
Комплексную (амплитудно-фазовую) частотную характеристику (КЧХ, АФХ) W(jw) аналитически легко получить по соответствующей передаточной функции, если положить Р = jw.
Путём выделения в выражении КЧХ вещественной U(w) и мнимой V(w) частей, получаются соответственно вещественная (ВЧХ) и мнимая (МЧХ) частотные характеристики
U(w) = ReW(jw);
V(w) = ImW(jw).
Модуль А(w) и аргумент j(w) КЧХ определяют соответственно амплитудную (АЧХ) и фазовую (ФЧХ) частотные характеристики
U(w) = modW(jw);
V(w) = argW(jw).
Между всеми частотными характеристиками имеют место очевидные соотношения:
W(jw) = U(w) + jV(w) ;
W(jw) = А(w) e jj (w) ;
А(w) = ÖU2(w) + V2(w) ;
V(w)
j(w) = arctg -------------- ;
U(w)
U(w) = А(w)cosj(w);
V(w) = А(w)sinj(w).
Применительно к САУ рис.3.1 при входном воздействии Df(t) частотные характеристики приведены на рис.6.1 и 6.2.
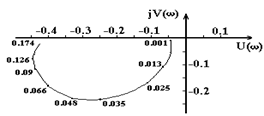 а)
а) 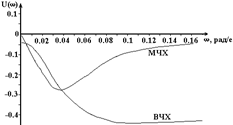 б)
б)
| U(w) | -0.03 | -0.04 | -0.06 | -0.08 | -0.11 | -0.17 | -0.25 | -0.33 | -0.4 | -0.44 | -0.44 |
| V(w) | -0.01 | -0.05 | -0.1 | -0.13 | -0.17 | -0.21 | -0.29 | -0.23 | -0.18 | -0.11 | -0.06 |
| w,рад/с | 0.001 | 0.005 | 0.01 | 0.013 | 0.018 | 0.025 | 0.035 | 0.48 | 0.066 | 0.09 | 0.13 |
Рис.6.1. Комплексная (а), вещественная (б) и мнимая (б) частотные характеристики САУ рис.3.1 при входном воздействии Df(t) и Ку = 20

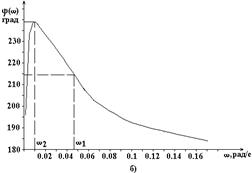
| w,рад/с | 0.001 | 0.005 | 0.01 | 0.013 | 0.018 | 0.025 | 0.035 | 0.048 | 0.066 | 0.09 | 0.13 |
| A(w) | 0.04 | 0.071 | 0.117 | 0.153 | 0.202 | 0.27 | 0.34 | 0.402 | 0.439 | 0.454 | 0.444 |
| j(w),град | 196 | 232 | 239 | 238 | 237 | 231 | 223 | 215 | 204 | 194 | 188 |
Рис.6.2. Амплитудная (а) и фазовая (б) частотные характеристики САУ рис.3.1 при входном воздействии Df(t) и Ку = 20, Кос = 20.
Из частотных характеристик следует, что при гармоническом характере возмущающего воздействия Df(t) влияние его на отклонение управляемой величины Dx(t) очень сильно возрастает с увеличением частоты. Например, при w1 = 0.047 рад/с и Df = 1.0sinw1t Dx(t) = 0.4sin(w1t + 2150), т. е. амплитуда колебаний Dxm = 0.4 имеет такое же значение, как и при отсутствии регулирования. Действительно, если в САУ рис.3.1 разорвать главную обратную связь, то будет
DX(P)
W(P) = ---------------- = - 0.4 ,
DF(P)
соответственно,
W(jw) = -0.4 и А(w) = 0.4.
При w > w1 влияние возмущающего воздействия сказывается ещё сильнее. Поэтому функционирование САУ рис.3.1 как системы регулирования будет эффективным только в том случае, если частота изменения возмущающего воздействия Df(t) будет достаточно малой (например, w1 < 0.01 рад/с). Из ФЧХ (рис.6.2,б) следует, что синусоидальные колебания величины на выходе Dx(t) опережают по фазе колебания Df(t) на угол больше 1800. Причем, при Ку = 20, Кос = 20 наибольший сдвиг фаз имеет место при w2 = 0.01 рад/с. Следует также отметить, что при w< w2 = 0.01 рад/с зависимость j(w) весьма резкая. Монотонный характер (без максимума) вещественной (рис.6.1,б) и амплитудной (рис.6.2,а) частотных характеристик свидетельствует о том, что при рассматриваемых параметрах (Ку = 20, Кос =20) скачкообразное изменение Df(t) вызывает монотонный (практически без перерегулирования и колебательности) переходный процесс Dx(t) (см.рис.5.3). На рис.6.3, 6.4 показаны КЧХ, ВЧХ, АЧХ и ФЧХ для случая, когда в качестве входного рассматривается задающее воздействие DZ(t). Характеристики построены при двух значениях Кос.

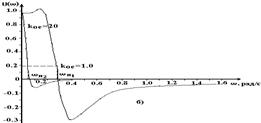
Кос = 1.0
| U(w) | 0.96 | 0.967 | 1.02 | 1.025 | 0.93 | 0.48 | -0.26 | -0.52 | -0.42 | -0.29 | -0.19 |
| V(w) | 0 | -0.26 | -0.46 | -0.67 | -1.0 | -1.38 | -1.23 | -0.66 | -0.3 | -0.14 | -0.07 |
| w,рад/с | 0 | 0.1 | 0.14 | 0.17 | 0.21 | 0.26 | 0.3 | 0.36 | 0.44 | 0.52 | 0.6 |
Кос = 20
| U(w) | 0.96 | 0.843 | 0.8 | 0.73 | 0.62 | 0.47 | 0.29 | 0.11 | -0.03 | -0.1 | -0.11 |
| V(w) | 0 | -0.27 | -0.34 | -0.42 | -0.5 | -0.57 | -0.58 | -0.53 | -0.42 | -0.28 | -0.16 |
| w,рад/с | 0 | 0.01 | 0.013 | 0.017 | 0.023 | 0.03 | 0.04 | 0.05 | 0.07 | 0.09 | 0.12 |
Рис.6.3. Комплексная (а) и вещественная (б) частотные характеристики САУ рис.3.1 при входном воздействии DZ(t), Ку = 20 и различных значениях Koc.

Кос = 1.0
| w,рад/с | 0 | 0.1 | 0.17 | 0.21 | 0.26 | 0.3 | 0.36 | 0.52 | 0.6 | 1.1 |
| A(w) | 0.96 | 1.0 | 1.22 | 1.37 | 1.46 | 1.26 | 0.84 | 0.32 | 0.2 | 0.06 |
| j(w),град | 0 | -15 | -33 | -47 | -71 | -102 | -128 | -154 | -160 | -170 |
Кос = 20
| w,рад/с | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.07 | 0.09 | 0.12 | 0.16 |
| A(ww) | 0.96 | 0.89 | 0.8 | 0.74 | 0.65 | 0.54 | 0.42 | 0/3 | 0.2 | 0.11 |
| j(w),град | 0 | -18 | -39 | -50 | -63 | -78 | -94 | -110 | -124 | -142 |
Рис.6.4. Амплитудная (а) и фазовая (б) частотные характеристики САУ рис.3.1 при входном воздействии DZ(t), Ку = 20 и различных значениях Koc.
Из рис.6.4,а видно, что при Кос = 1.0 АЧХ имеет ярко выраженный максимум при частоте wр = 0.26 рад/с. Это свидетельствует о колебательном характере переходной характеристики (см.рис.5.2).
Причём, колебательность составляет [1]:
Aмакс 1.46
G = ------------- = --------------- = 1,52.
А(о) 0.96
При этом время переходного процесса имеет значение
2p 2*3,14
tп » (1 ¸ 2) -------- = (1 ¸ 2) -------------- = 24 ¸ 48с
wр 0.26
и на этом интервале времени имеют место 1 ¸ 2 колебания. Время достижения первого максимума составляет
p 3.14
tмакс »---------- = ----------------- = 6с.
2wр 2*0.26
О повышенной колебательности САУ рис.3.1 при Кос = 1.0 свидетельствует также наличие отрицательного минимума у ВЧХ (рис.6.3,б). При этом перерегулирование имеет значение [1]:
1.18Uмакс - U(0) 1.18 * 1.025 - 0.96
< -------------------------------- 100% = ------------------------ *100% = 53.6%.
U(0) 0.96
Время переходного процесса определяется шириной характеристики U(w), ограниченной значением частоты wп (рис.6.3,б), при котором положительная часть U(w) становится меньше 0.2U(0) = 0.2*0.96 = 0.192. Величину wп называют интервалом положительности U(w). При этом
p 3.14
tп ³ (1 ¸ 4) ------------- = (1 ¸ 4) -------------- = 12 ¸ 48с.
wп1 0.26
При Кос = 20 ВЧХ (рис.6.3,б) и АЧХ (рис.6.4,а) не имеют максимумов при w>0, что свидетельствует об отсутствии перерегулирования (см.рис.3.2). Однако, при этом существенно увеличивается (по сравнению с Кос = 1.0) время переходного процесса (wп2 < wп1) иуменьшается частотная полоса пропускания задающего воздействия (w £ 0.02 рад/с). Это может неблагоприятно сказаться на функционировании САУ, если задающее воздействие для неё будет формироваться автоматически как результат функционирования системы управления более высокого иерархического уровня. При высокой частоте изменения воздействия DZ(t) САУ (при Кос = 20) будет отрабатывать задания с большой погрешностью.
При ручном формировании задающего воздействия уменьшение полосы пропускания по нему и увеличение времени переходного процесса могут не иметь существенного значения. Поэтому целесообразно принять Кос = 20, что обеспечивает переходный процесс, близкий к экспоненциальному, как при воздействии DZ(t), так и при Df(t).
Похожие работы
... Вид характеристики зависит от свойств самого регулятора, характеристик ИО и ОР. Вопросы устойчивости, характеризующейся динамическими свойствами АСР, являются основными при изучении теории и эксплуатации средств автоматического регулирования. Определение температуры является одним из сложных и трудоемких процессов измерения, основанным на теплообмене между телами. Приборы, входящие в тепловой ...
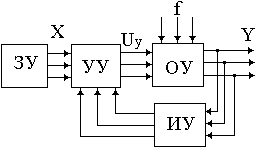
... поведение регулируемой величины. Управляющее воздействие вырабатывается устройством управления (УУ). Совокупность взаимодействующих управляющего устройства и управляемого объекта образует систему автоматического управления. Система автоматического управления (САУ) поддерживает или улучшает функционирование управляемого объекта. В ряде случаев вспомогательные для САУ операции (пуск, остановка, ...
... значениях функции. Начальное значение функции:. (2.10) Конечное значение функции: . (2.11) 7. Теорема запаздывания . (2.12) 4. Дифференциальные уравнения САУ При математическом описании систем автоматического управления составляют уравнения статики и динамики. Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими. Уравнения динамики ...
... можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость. Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением. Построение области ...


0 комментариев